模拟退火
最早但最流行的元启发式算法之一是模拟退火(simulated annealing,SA),它是一种基于轨迹的全局优化随机搜索技术。它模仿金属材料加工中的退火过程,当金属以最小的能量、较大的晶体尺寸冷却并冻结成结晶状态时,可以减少金属结构中的缺陷。退火过程包括仔细地控制温度和冷却速度,通常称为退火制度(annealing schedule)。 SA 已经成功应用于许多领域。
退火与玻尔兹曼分布
自 Kirkpatrick 等人首次开发出模拟退火以来 [7],SA 已经应用于几乎所有的优化领域。名词 SA 来自金属加工的退火特性。然而,SA 本质上与 Metropolis 等人提出的经典的 Metropolis 算法 [8] 具有很强的相似性。
与具有陷入局部最小值的缺点的基于梯度的(gradient-based)方法以及其他确定性搜索方法不同,SA 的主要优势在于其具有避免陷入局部最小值的能力。事实上,已经证明,如果足够的随机性与非常缓慢的冷却结合使用,模拟退火将收敛到其全局最优性。实质上,SA 是一种搜索算法,可以视为马尔可夫链,能够在合适的条件下收敛。
打个比方,这相当于将一些弹跳球放在某种景观(landscape)上,当球弹跳并失去能量时,它们会稳定在某个局部最小点。如果球能够反弹足够长的时间且足够慢地失去能量,那么一些球将最终落入全局最低的位置,因此可以达到全局最小值。
SA 算法的基本思想是用马尔可夫链的形式进行随机搜索,它不仅接受改善目标函数的变化,而且还能保留一些不理想的变化。例如,在最小化问题中,任何能够降低目标函数 $f$ 的值的改变或移动会被接受。然而,一些增加 $f$ 的值的改变也会以概率 $p$ 接受。这个概率 $p$ 也被称为转移概率(transition probability),由下式确定
$$p = exp \bigl [ - \frac{\Delta E}{k_B T} \bigr ], \tag {1}$$
其中 $k_B$ 是玻尔兹曼常数,为简单起见,我们可以设 $k_B=1$。$T$ 是控制退火过程的温度。$\Delta E$ 是能级变化。该转移概率基于统计力学中的波尔兹曼分布(Boltzmann distribution)。
将 $\Delta E$ 与目标函数的变化 $\Delta f$ 关联起来最简单的方法是使用
$$\Delta E = \gamma \Delta f, \tag 2$$
其中 $\gamma$ 是一个实常数。为了简单而不失一般性,我们可以用 $k_B = 1$、$\gamma = 1$。由此,概率 $p$ 变为
$$p(\Delta f, T) = e^ {-\Delta f / T}. \tag 3$$
无论是否接受改变,通常都会使用随机数 $r$ 作为阈值。因此,如果 $p \lt r$ 或
$$p = exp \bigl [- \frac{\Delta f}{T} \bigr] \gt r, \tag 4$$
则接受移动/改变。大多数情况下,$r$ 服从 $[0, 1]$ 上的均匀分布。
参数
选择正确的初始温度至关重要。对于给定的改变 $\Delta f$,如果 $T$ 太高($T \to \infty$),那么 $p \to 1$,这意味着几乎所有的改变都会被接受。如果 $T$ 太低($T \to \infty$),那么由于 $p \to 0$,将会仅有极小的 $\Delta f \gt 0$ (更差的解)被接受。因此解的多样性被限制,但任何改善的 $\Delta f$ 都会被接受。事实上,$T \to 0$ 的特殊情况,对应于基于梯度的方法,因为只接受更好的解,且系统基本上沿着坡爬升或下降。因此,如果 $T$ 太高,系统在拓扑上处于高能状态,且不容易达到最小值。如果 $T$ 太低,系统可能会陷入局部最小值(不一定是全局最小值),没有足够的能量跳出局部最小值来探索其他最小值(包括全局最小值)。所以,应该选择一个合适的初始温度。
另一个重要问题是如何控制退火或冷却过程,使系统从较高的温度逐渐冷却,最终冻结(freeze)到全局最小状态。控制冷却速度或降低温度的方法有很多种。
两种常用的退火制度(或冷却制度)是线性的和几何的。对于线性冷却制度,我们有
$$T = T_0 - \beta t, \tag 5$$
或 $T \to T - \delta T$,其中 $T_0$ 是初始温度,$t$ 是迭代伪时间。$\beta$ 是冷却率,当 $t \to t_f$(或者最大迭代次数 $N$)、 $T \to 0$ 时,通常令 $\beta = (T_0 - T_f) / t_f$。
另一方面,几何冷却制度本质上通过冷却因子 $0 \lt \alpha \lt 1$ 降低温度,因此用 $\alpha T$ 替换 $T$,或者
$$T(t) = T_0 \alpha^t, \quad t=1, 2, …, t_f. \tag 6$$
第二种方法的优点是当 $t \to \infty$ 时 $T \to 0$,因此不需要指定最大迭代次数。出于这个原因,我们将使用几何冷却制度。冷却过程应该足够慢以使系统容易稳定。实际中,通常使用 $\alpha = 0.7 \sim 0.99$。
另外,对于给定的温度,需要对目标函数进行多次评估(evaluation)。如果评估次数过少,系统可能会有不稳定的(进而不会收敛到全局最优)风险。如果评估次数过多,则需要耗费大量时间,且系统通常会收敛得太慢,因为要达到稳定性的迭代次数可能与问题规模成指数关系。
因此,评估次数和解的质量之间有一个很好的平衡。我们既可以在少数几个温度水平上进行多次评估,也可以在多个温度水平下进行少量评估。有两种主要方法来设置迭代次数:固定的或变化的。第一种是在每个温度下使用固定次数的迭代;第二种是在较低温度下增加迭代次数,以便可以充分探索局部最小值。
SA 算法
模拟退火算法可以概括为下图所示的伪代码。

要找到合适的起始温度 $T_0$,我们可以使用任何关于目标函数的信息。如果我们知道目标函数的最大改变 $max(\Delta f)$,我们可以用它来估计给定概率 $p_0$ 的初始温度 $T_0$。即,$T_0 \approx - \frac{max(\Delta f)}{ln \; p_0}$。
如果我们不知道目标函数可能的最大改变,我们可以使用启发式方法。我们可以从非常高的温度开始评估(以便接受几乎所有的改变)并快速降低温度,直到大约 50% 或 60% 的较差移动/改变被接受,然后将此温度用作适当的新初始温度 $T_0$ 且相对较慢的冷却。
对于最终的温度,理论上它应该为零,以便不会接受更差的移动。但是,如果 $T_f \to 0$,则需要更多不必要的评估。在实践中,我们只需选择一个非常小的值,例如 $T_f = 10^{-10 } \sim 10^{-5}$,取决于解所需的质量和时间的限制。
无约束优化
基于选择冷却速率、初始和最终温度以及平衡的迭代次数等重要参数的指导原则,我们可以使用 Matlab 和 Octave 来实现模拟退火。
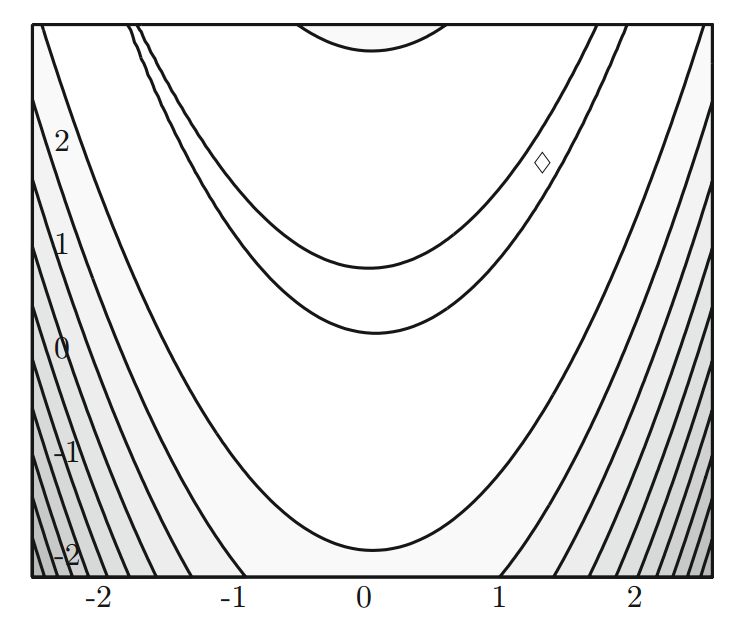
对于 Rosenbrock 香蕉函数 $f(x,y) = (1 - x)^2 + 100 (y - x^2)^2$,我们知道它的全局最小值 $f_* = 0$ 出现在 (1, 1) 处(见下图)。这是一个标准测试函数,且对于大多数算法来说寻优非常困难。
但是使用 SA 我们可以很容易地找到这个全局最小值,最后的 500 次退火评估如下图所示。
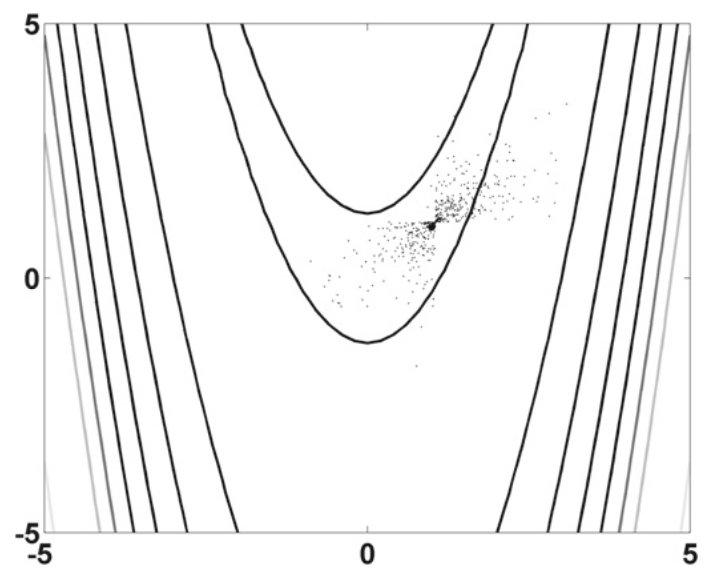
这种香蕉函数还是比较简单的,因为它有弯曲的窄谷。我们应该对广泛的测试函数进行验证,特别是那些具有高度多峰和高度非线性的测试函数。
基本收敛特性
对于模拟退火及其变种的收敛特性有相对广泛的研究 [1, 2, 4]。本节中的描述主要基于 Bertsimas 和 Tsitsiklis 在 1993年 的分析 [1]。
我们假设 SA 中的解形成了有限集合 $S$,并且在这个有限集合 $S$ 上定义了一个实值目标函数 $f$。我们还假设 $S$ 有一个合适的子集 $S_*$,使得 $S_* \subset S$ 、$f$ 在 $S_*$ 实现全局最小。迭代从初始状态 $x_0 \in S$ 开始。
对于每个 $i \in S$,我们可以定义 $i$ 的一组邻居为 $S_i \subset S - {i}$。另外,冷却制度 $T(t)$ 被定义为非增函数 $T$,使得当 $t$ 很大时温度 $T(t)$ 接近于零。在这种情况下,SA 成为离散时间非均匀马尔可夫链 $x(t)$。从当前状态 $i$ 开始随机选择一个 $i$ 的邻居 $j$,选择任意 $j \in S_i$ 的概率被定义为 $q_{ij}$。
此外,对于每一个 $i$,$j \in S_i$ 的所有正系数 $q_{ij}$ 满足 $\sum_{j \in S_i} = q_{ij} = 1$。如果我们假设马尔可夫链 $x(t)$ 是非周期且不可约的(即,对于所有$i$、$j$,$q_{ij} = q_{ji}$),那么这个马尔可夫链也是可逆的。在这种情况下,对于 $i \in S$,其相应的不变概率(invariant probability)可以由所谓的吉布斯分布(Gibbs distribution)给出
$$\pi_T(i) = \frac{1}{Q_T}e^{-f(i)/T} \tag 7$$
这里 $Q_T$ 是一个归一化常数 [1]。如果我们让 $T(t)$ 保持在恒定值 $T$,这个关系可以被理解。可以预期当 $T \to 0$ 时,这个概率集中在 $S_*$。
一个基本问题是,由 $x(t)$ 构成的迭代或马尔可夫链是否会收敛到最优集合 $S_*$?如果是,收敛速度有多快?如果不是,确保收敛所需的条件是什么?
根据 Hajek(1988)和 Hajek 与 Sasaki(1989)[4, 5] 的研究,在以下条件下,SA 算法可以统计意义上的收敛:
$$\lim_{t \to \infty} T(t) = 0, \quad \sum_{t=1}^{\infty} exp \bigl [ - \bar h / T(t) \bigr] \to \infty, \tag 8$$
其中 $\bar h \gt 0$ 是使得每个 $i \in S$ 在高度 $\bar h$ 处与 $S_*$ 通信的最小数值。这里,“状态 $i$ 在高度 $\bar h$ 处与 $S$ 通信”的含义定义如下:$S$ 中存在一条路径(path),开始于状态 $i$ 结束于 $S_*$ 的某个状态,沿着这条路径,$f$ 的最大值为 $f + \bar h$。值得指出的是,这种收敛是以概率 $P$ 收敛,而不是几乎确定的收敛。即,
$$\lim_{t \to \infty} P(x(t) \in S_*) \to 1, \tag 9$$
这也需要隐式地指出,如前所述,马尔科夫链 $x(t)$ 是非周期不可约的。
为了满足这两个条件,我们可以使用最广泛使用的冷却制度之一:
$$T(t) = \frac{h}{log ; t}, \tag {10}$$
这可以得出,当 $t \to \infty$ 时 $T(t) \to 0$,且
$$\sum_{t=1}^{\infty} exp \bigl [ - \bar h / T(t) \bigr] = \sum_{t=1}^{\infty} \frac{1}{t^{\theta}}, \quad \theta = \frac{\bar h}{h}, \tag {12}$$
如果 $\theta = \bar h / h \le 1$,那么它接近于 $\infty$。即,当且仅当时 $h \ge \bar h$ 时,SA 才会收敛。在这种情况下,马尔可夫链是可逆和齐次的。这也意味着近似的策略 $\tilde T(t)$ 到 $T(t) = h / log \; t$ 可以用:
$$\tilde T(t) = \frac 1k, \quad \text{for $t \in [t_k, t_{k+1}]$}, \tag {13}$$
其中
$$t_{k+1} = t_k + exp(kh), \tag {14}$$
从 $t_1 = 1$ 开始。
现在让我们根据马尔可夫链的特征值对 SA 进行简要分析。马尔可夫链的第一个特征值 $\lambda_1$ 始终为 $\lambda_1 = 1$。收敛速率通常由第二大特征值 $\lambda_2$ 决定。Chiang 和 Chow [3] 证明 SA 中转移概率矩阵的特征值是实数,其弛豫时间(relaxation time)与 $\lambda_2$ 有关 [3]。事实上,在目标函数 $f$ 具有唯一的全局最小值的情况下,该弛豫时间可以用 $exp(kh)$ 来近似。换句话说,收敛条件 $h \ge \bar h$ 意味着区间 $[t_k,t_{k + 1}]$ 有一个弛豫时间 $exp[k(\bar h - h)]$,这样,当 $k \to \infty$ 时 $\pi(i)|_ {t_{k+1}}$ 非常接近不变概率 $\pi_T = 1/ k(i)$。
了解 SA 工作原理的另一种方法如下:对于深度为 $h$ 的局部最小值,沿任何特定路径从该局部最小值逸出的概率至多为 $exp(- h/T)$。因此,如果候选路径的数量足够多,则整体逃生概率可能是显著的。这就是为什么目标函数的景观以及状态空间的结构在确定搜索系统行为时重要的部分原因。
实践中的 SA 行为
现在我们可以在实践中讨论这种收敛结果的真正含义。从实践的角度来看,如果我们运行 N 步 SA,概率 $P(x(N) \in S_*)$ 可能不会有任何用处。事实上,我们可能更关心在 $t \ge N$ 期间没有访问到 $S_*$ 中的状态的估计概率。根据 Bertsimas 和 Tsitsiklis [1],$T(t) = h/log \; t$ 的概率可近似为
$$max ; P \bigl [ x(t) \not \in S_* | x(0) \bigr ] \ge \frac{A}{t^a}, \tag {15}$$
其中 $A$ 和 $a$ 是取决于目标 $f$ 和邻域结构的正常数。显然,当 $t = N \to \infty$ 时,这个概率 $A/t^a \to 0$。换句话说,随着迭代的进行,不发现全局最优性的概率接近零。
尽管这些理论结果可能是严格的,但真正的含义可能不那么容易解释。实际上,运行一个很长时间的(当然不是 $t \to \infty$)算法是不现实的。此外,收敛速度还取决于目标函数的景观和邻域的结构。因此,何时停止执行算法以及算法实际上如何运行的可能是一个非常不同的问题。
各种研究和大量的应用表明,SA 的性能相当混杂。对于一些问题,SA 可以胜过最好的已知方法,而对于其他问题,专门的启发式算法可以比 SA 好 [1]。对于诸如图划分问题、图着色问题和旅行商问题等应用来说,情况也是如此。
另外,计算时间通常很长,因为 SA 通常需要大量的迭代。对于某些应用(如图像处理),计算时间可能会相当长。
另一方面,许多研究人员提出的一个常见问题是,不同的冷却制度对性能有什么影响?据观察,当冷却制度改变时,约 10% 的计算工作可能是典型的 [9]。其他研究表明,大约 40% 的计算变量是可能的 [11]。这激发了非单调冷却制度和许多其他研究,例如并行退火和并行回火。
值得指出的是,SA 的性能也与马尔可夫链的混合能力有关。在非常高的温度下,马尔可夫链会发生快速混合,导致随机行走。然而,对于低得多的温度,尽管事实上小温度下的行为与 SA 算法最相关,但为 SA 马尔可夫链提供快速混合仍然是一项非常具有挑战性的任务。
随机隧道
为确保模拟退火的全局收敛,必须使用适当的冷却制度。当函数景观复杂时,如果温度过低,SA 可能越来越难以摆脱局部最小点。像所谓的模拟回火(simulated tempering)一样,提高温度可以解决问题,但收敛速度通常较慢,计算时间也会增加。
随机隧道(stochastic tunneling)使用隧道思想将目标函数景观转化为一种不同但更方便的方法 [6, 10]。其实质是构造一个非线性变换,使 $f(x)$ 的某些模式被抑制,其他模式被放大,同时保留 $f(x)$ 的极小点轨迹。
这种隧道变换的标准形式是
$$g(x) = 1 - exp [- \gamma (f(x) - f_0)], \tag {16}$$
其中 $f_0$ 是目前发现的 $f(x)$ 的当前最低值。 $\gamma \gt 0$ 是缩放参数,$g$ 是变换的新景观。通过这个简单的变换,我们可以看到,当 $f - f0 \to 0$ 时,即 $f_0$ 接近真正的全局最小值时 $g \to 0$。另一方面,如果 $f \gg f_0$,则 $g \to 1$,这意味着远高于当前最小值 $f_0$ 的所有模式都被抑制。对于一个简单的一维函数,很容易看到这些属性确实保留了函数的轨迹(见下图)。
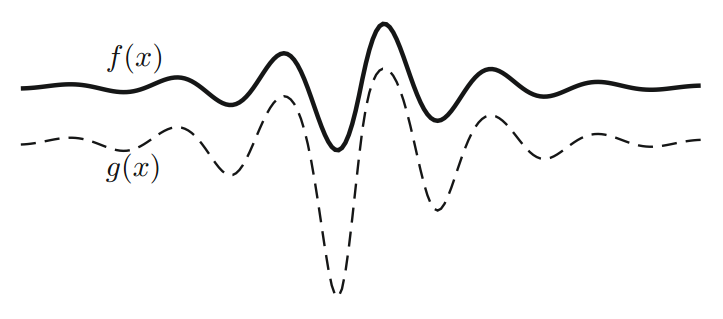
由于保留了最小值的轨迹,当前最低值 $f_0$ 以上的所有模式都被抑制到一定程度,而 $f_0$ 以下的模式被放大,这使系统更容易摆脱局部模式。模拟和研究表明,它可以显著地改善具有复杂景观和模式的函数的收敛性。
SA 描述主要针对无约束的问题。但是,对于受限制的问题,我们需要找到一种处理约束的实用方法,因为大多数现实世界的优化问题都受到限制。通常的方法,如罚函数法(penalty methods)可以用于处理约束,我们将在后面详细讨论非线性约束的方法。
参考文献
[1] Bertsimas D, Tsitsiklis J. Simulated annealing. Stat Sci 1993;8(1):10–5.
[2] Cerny V. A thermodynamical approach to the travelling salesman problem: an efficient simulation algorithm. J Optim Theory Appl 1985;45(1):41–51.
[3] Chiang TS, Chow Y. On the eigenvalues and annealing rate. Math Oper Res 1988;13(3):508–11.
[4] Hajek B. Cooling schedules for optimal annealing. Math Oper Res 1988;13(2):311–29.
[5] Hajek B, Sasaki G. Simulated annealing—to cool or not. Syst Control Lett 1989; 12(4):443–7.
[6] Hamacher K, Wenzel W. The scaling behaviour of stochastic minimization algorithms in a perfect funnel landscape. Phys Rev E 1999;59(2):938–41.
[7] Kirkpatrick S, Gelatt CD, Vecchi MP. Optimization by simulated annealing. Science 1983;220(4598):671–80.
[8] Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E. Equations of state calculations by fast computing machines. J Chem Phys 1953;21(6):1087–92.
[9] van Laarhoven P, Aarts E. Simulated annealing: theory and applications. Dordrecht, Netherland: Kluwer Academic Publishers/D. Reidel; 1987.
[10] Wenzel W, Hamacher K. A stochastic tunneling approach for global optimization. Phys Rev Lett 1999;82(15):3003–7.
[11] Yang XS. Biology-derived algorithms in engineering optimization. In: Olariu S, Zomaya AY, editors. Handbook of bioinspired algorithms and applications. Boca Raton, FL, USA:Chapman & Hall/CRC; 2005. [chapter 32].