遗传算法
就其应用的多样性而言,遗传算法是最受欢迎的进化算法之一。遗传算法已经被尝试用于绝大多数众所周知的优化问题。另外,遗传算法是基于群体的,许多现代的进化算法直接基于遗传算法或具有一些强烈的相似性。
介绍
John Holland 和他的合作者在 20 世纪 60 年代和 70 年代,基于达尔文的自然选择理论的生物进化模型,开发了遗传算法(Genetic algorithm,GA)[11, 4] 。Holland 可能是第一个在自适应和人工系统研究中使用交叉、重组、变异和选择的人。作为解决问题的策略,这些遗传算子构成遗传算法的基本部分。从那以后,遗传算法的许多变体被开发出来,并且被应用于各种各样的优化问题,从图着色到模式识别,从离散系统(如旅行商问题)到连续系统(如航空航天工程领域,翼型的有效设计),从金融市场到多目标工程优化。
遗传算法与传统优化算法相比有许多优点。两个最显著的是,处理复杂问题和并行化的能力。遗传算法可以处理各种类型的优化,无论目标(适应度)函数是平稳还是非平稳(随时间变化),线性还是非线性,连续或不连续,或者有随机噪声。由于群体的后代行为如同独立的代理,所以群体(或任何小组)可以同时在多个方向探索搜索空间。这个特性使得实现并行化算法变得非常理想。不同的参数甚至不同的编码字符串组可以同时操作。
但是,遗传算法也有一些缺点。适应函数的制定,人口规模的使用,突变和交叉率等重要参数的选择以及新群体的选择标准应当小心执行。任何不恰当的选择都会使算法难以收敛,产生无意义的结果。尽管存在这些缺陷,遗传算法仍然是现代非线性优化中使用最广泛的优化算法之一。
遗传算法
遗传算法的实质是将优化函数编码为代表染色体的比特(bits)或字符串数组,遗传算子(genetic operator)对字符串进行操作,并根据其适应性进行选择,以便找到有关问题的好的(甚至是最佳的)解。
这通常通过以下过程完成:
- 对目标或代价(cost)函数进行编码;
- 定义适应度函数或选择标准;
- 创建种群、个体;
- 通过评估种群中所有个体的适应度来完成进化周期(evolution cycle)或迭代,通过进行交叉和变异,适应性比例繁殖等来创建一个新种群,并替换旧种群并重新迭代新的种群;
- 解码结果以获得问题的解。
这些步骤可以用下图所示的遗传算法的伪代码来表示。

创造新种群的一次迭代被称为一代。尽管已经对可变长度字符串和编码结构进行了大量研究,但是在大多数遗传算法中都使用固定长度字符串。目标函数的编码通常是自适应遗传算法中二进制数组或实数数组的形式。为了简单起见,我们在讨论中使用二进制字符串进行编码和解码。遗传算子包括交叉、变异和选择。
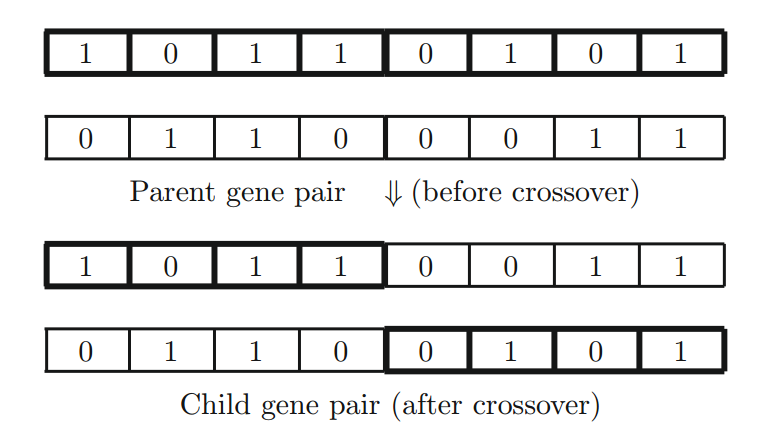
具有较高概率 $p_c$ 的两个父字符串的交叉是主算子,通过将一条染色体的一个片段与另一个染色体上的相应片段随机交换来进行(见下图)。以这种方式进行的交叉是单点交叉(single-point crossover)。交叉也可以发生在多个位置,基本上是将多个片段与其相应染色体上的片段交换。遗传算法中更多的是使用多点交叉来增加算法的进化效率。
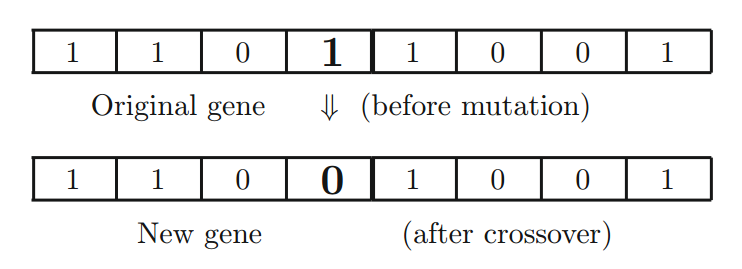
变异操作是通过随机选择的比特来实现的(见下图),变异概率 $p_m$ 通常很小。另外,突变也可能在多个位点同时发生,这在实践和实现中可能是有利的。
种群中个体的选择是通过对个体的适应性进行评估来实现的,如果达到某个特定的阈值,它可以留在新一代中。此外,选择也可以是基于适应性的,以便种群的繁衍是适应度比例选择的(fitness-proportionate)。也就是说,具有较高适应性的个体更容易繁殖。
遗传算子的作用
如前所述,遗传算法有三种主要的遗传算子:交叉、变异和选择。他们的作用各有不同。
- 交叉(Crossover)。将染色体或解中的一部分解与另一部分解交换。主要作用是提供解的混合和子空间中的收敛。
- 变异(Mutation)。解的一部分随机变化,这增加了种群的多样性,并提供逃离局部最优化的机制。
- 选择或精英主义(Selection of the fittest, or elitism)。高质量解将传给下一代,这通常是通过某种形式的选择最佳解来进行的。
显然,在实际算法中,这些遗传算子之间的相互作用使得行为非常复杂。但是,各个组件的作用保持不变。
交叉主要是一个在子空间的行为。对于一个由 a 和 b 组成的二进制字符串系统来说,这一点变得很清楚。例如,对于两个字符串 $S_1 = [aabb]$ 和 $S_2 = [abaa]$,无论交叉如何进行,它们的后代总是以 [a…]。也就是说,交叉只能产生第一个分量始终为 a 的子空间中的解。此外,不管交叉如何应用,两个相同的解都会产生两个相同的后代。这意味着交叉作用在子空间,并且收敛的解/状态将保持收敛。
另一方面,变异通常会产生子空间外的解。对于前面的例子,如果变异出现在第一个 a 上并且跳变为 b,那么解 $S_3 = [babb]$ 不属于前面的子空间。事实上,通常突变产生的解会远离当前的解,从而增加了群体的多样性。这使得群体能够摆脱局部最优。
一个重要问题是种群中的随机选择。群体中的交叉需要双亲(parents)。我们是随机选择还是偏向更好的解?一种方法是使用轮盘(roulette wheel)来做选择;另一种是使用适应度比例选择。显然,还有其他形式的选择,包括线性排序选择,竞赛选择等。
交叉和变异都可以在不使用目标或适应度景观(landscape)知识的情况下工作。另一方面,优胜劣汰或精英主义的选择确实使用适应度景观作为指导原则,从而影响算法的搜索行为。选择什么解以及如何选择解取决于算法以及目标函数值。这种精英主义确保最好的解必须在群体中保留。然而,非常强大的精英主义可能会导致过早收敛。
值得指出的是,这些遗传算子是基础。其他算子可能采取不同的形式,也可以使用混合算子。但是,为了理解遗传算法的基本行为,我们将关注这些关键算子。
参数的选择
一个重要的问题是制定或选择合适的适应度函数,以确定特定问题中的选择标准。为了使用遗传算法来最小化函数,构建适应度函数的一个简单方法是使用最简单的形式 $F = A - y$,其中 $A$ 是一个大的常数(如果适应度不要求为非负,那么 $A = 0$ 也是可以的)且 $y = f(x)$。因此,目标是最大化适应度函数以使目标函数 $f(x)$ 最小化。另外,对于最小化问题,可以定义一个适应度函数 $F = 1 / f(x)$,但当 $f \to 0$ 时它可能具有奇异性。定义适应度函数的方法有很多。例如,我们可以使用与整个群体相关的个体适应度分配,
$$F(x_i) = \frac{f(\xi_i)}{\sum_{i=1}^n f(\xi_i)} \tag 1$$
其中 $\xi_i$ 是个体 $i$ 的表型值(phenotypic value)、$n$ 是群体规模。
适应度函数的适当形式将确保高效地选择具有较高适应度的解。适应度函数差可能导致解不正确或毫无意义。
另一个重要问题是各种参数的选择。交叉概率 $p_c$ 通常非常高,通常在 0.7 〜 1.0 的范围内。另一方面,变异概率 $p_m$ 通常很小(通常为 0.001 〜 0.05)。如果 $p_c$ 太小,那么交叉就会稀疏地发生,这对于进化是不利的。如果变异概率太高,即使最佳解即将到来,解仍然可能“跳来跳去”。
选择最佳解的适当标准也很重要。如何选择当前的种群,以便保留较高适应度的优秀个体并传递给下一代,这是一个尚未完全解答的问题。选择往往是与某些精英主义联系在一起进行的。最基本的精英主义是选择最合适的个体(每一代),其特征将被遗传算子传递到下一代。这确保更快地到达最佳解。
其他问题包括多变异位点和各种群体规模的使用。单位点的变异并不十分有效;多位点的变异将增加进化效率。然而,太多的变异会使系统很难收敛,甚至会使系统陷入错误的解。在真实的生态系统中,如果在高选择压力下变异率过高,整个种群可能会灭绝。
此外,正确种群规模 $n$ 的选择也非常重要。如果种群规模太小,没有足够的进化发展,整个种群就有可能灭绝。在现实世界中,对于种群规模较少的物种而言,生态学理论认为这种物种确实存在灭绝危险。即使系统继续运行,仍然存在过早收敛的危险。在在一个小群体中,如果一个明显更适应(fit)的个体出现得太早,它可能会繁殖出足够多的后代,使他们压倒整个(小)群体。这最终将使系统达到局部最优(而不是全局最优)。另一方面,如果群体过多,则需要对目标函数进行更多的评估,这将花费大量计算时间。研究和实证观察表明,n = 40 到 200 的种群规模适用于大多数问题。
此外,对于更复杂的问题,可以使用各种 GA 变体来执行特定的任务。文献中可以找到自适应遗传算法和混合遗传算法等变体。
使用所描述的基本过程,我们可以用任何编程语言实现遗传算法。从实现的角度来看,有两种使用编码字符串的主要方式。我们可以对群体中的每个个体使用单独的字符串(或多个字符串),也可以对所有个体或变量使用一个长字符串,如下图所示。
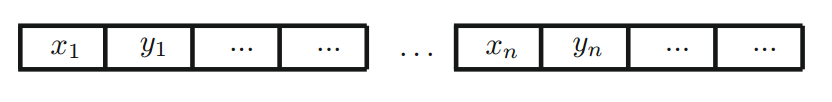
著名的 Easom 函数
$$f(x) = - cos(x) e ^{- (x - \pi)^2}, \quad x \in [-10, 10] \tag 2$$
在 $x_* = \pi$ 处具有全局最大值 $f_{max} = 1$。典型运行的输出如下图所示,其中上图显示最佳估计 $x_* \to \pi$ 的变化,下图显示适应度函数的变化。
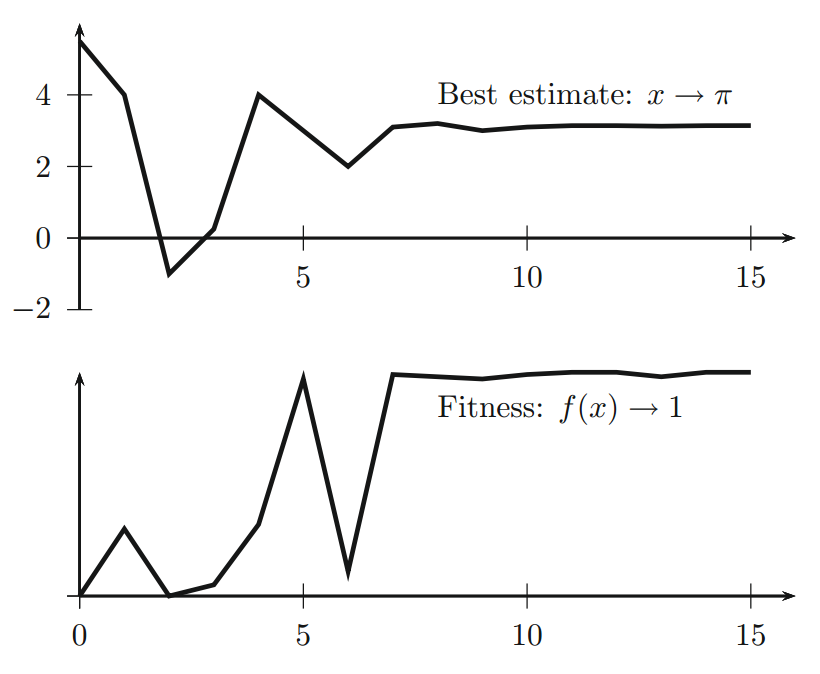
遗传算法被广泛使用,几乎所有的编程语言都有很多软件包。有效的实现可以在商业和自由代码中找到。出于这个原因,我们在这里不提供任何实现。
GA 变体
有几十个 GA 变体可以统称为遗传算法。许多变体都基于基本遗传算子的各种修改。
对于交叉算子,除了多位点或N-位点交叉与一致交叉外,洗牌交叉(shuffled crossover)使用两个父代 N 个点处的随机置换,然后通过逆置换将混合的子代置换回来。同样,变异可以通过随机选择位点来实现;通过逐位反转,反转整个字符串;或随机变异,字符串以概率 $p_m$ 替换为新字符串。再次,精英主义也可以采取许多不同的形式。所有这些方法在遗传算法的形式和行为上引入了轻微的变化。
在所有这些变体中,字符串/位的长度,交叉和变异概率以及种群规模都是固定的。这种固定没有强有力的理由。另一方面,如果我们允许这些参数变化,比如种群规模和字符串长度,我们可以有自适应遗传算法。突变率也可以根据种群的变化而改变。例如,如果种群中的解在一定数量的迭代或代数中没有改进,则可以暂时增加突变率。Sharapov [15] 进行了较为全面的综述。
遗传算法可以与其他算法混合使用。例如,可以使用基于梯度的方法来增强遗传算法的性能。遗传算法的全局搜索能力用于确保以高可能性发现全局最优性,而导数或局部信息可用于加速局部搜索。对于这种方法,可以将遗传算法与各种其他算法结合使用以利用各自算法的优点。
基本的遗传算子可以用来演化计算机代码和其他问题,形成更一般的进化计算[5, 13]。
正如我们在前面的章节中指出的那样,算法是自组织的,遗传算法中的参数可以被调整,一些所谓的自组织遗传算法也可以开发出来。事实上,遗传算法有许多变种,感兴趣的读者可以参考更多专业文献。
模式定理
遗传算法的重要理论结果之一可能是 Holland 的模式定理(schema theorem),源自 John Holland 的原创工作 [11]。
粗略地说,模式(schema)是一个只包含 0、1 或 * 模板字符串。在这里,符号 * 是一个通配符,它可以取任何等位基因(allele)值(0 或 1)。因此,H = 1*0**1* 是一个表示 $2^4 = 16$ 个不同基因序列的染色体集合的模式,所有的这些都以 [1*0**1*] 的形式出现,其中四个 * 可以取 0 或 1。在这个意义上,模式是用模板 $H$ 表示的所有可能基因空间的子集。
模式的阶(order)是模式中非 * 的数量,通常记为 $o(H)$。在我们的例子中,$o(H) = 3$。另外,模式 $H$ 的定义长度 $\delta (H)$ 定义为模式中第一个和最后一个非 * 基因之间的距离。在我们的例子中,第一个是 1,最后一个也是 1,因此 $\delta(H) = 5$。值得指出的是,1 * * 1 和 1 0 * 1 具有相同的定义长度 3,而 1 0 * * 定义长度为 1,* 1 * * 的定义长度为 0。给定长度为 m 的模式字符串,其定义长度总是小于或等于字符串长度 m。即,$\delta (H) \le m$。
Holland 的适应度比例选择算子可以定义为个体 $h$ 对模式 $H$ 进行抽样的概率 $p$,
$$p (h \in H) = \frac{k_{H,t} \bar f(H, t)}{n \bar f(t)} \tag 3$$
其中 $n$ 是种群规模、$\bar f(t)$ 是第 t 代的平均适应度,
$$\bar f(t) = \frac 1n \sum_{i=1}^n f_i \tag 4$$
这里,$k_{H,t}$ 是第 t 代个体匹配模式 $H$ 的数量,$\bar f(H, t)$ 是第 t 代与模式 $H$ 匹配的个体或实例的平均适应度。
因此,$H$ 的实例的期望或预期数量变成
$$E[k_{H, t+1}] = n \; p(h \in H) = \frac{k_{H,t} \bar f(H, t)}{\bar f(t)} \tag 5$$
著名的模式定理可以表述如下:
$$E[k_{H, t+1}] \ge k_{H, t} \frac{\bar f(H, t)}{\bar f(t)} \bigl [ 1 - p_c \frac{\delta (H)}{m - 1}\bigr] (1 - p_m)^{o(H)} \tag 6$$
其中 $p_c$ 和 $p_m$ 分别为交叉概率和变异概率。在单点交叉和逐基因变异的情况下,该不等式总是适用于任何模式 $H$。
如果我们假设 $p_m \ll 1$,前面的公式可以近似写成
$$E[k_{H, t+1}] \ge k_{H, t} \frac{\bar f(H, t)}{\bar f(t)} \Bigl [ 1 - \frac{\delta (H)}{(m - 1)} p_c - o(H) p_m \Bigr] \tag 7$$
这个定理意味着具有高于平均水平的低阶图更可能在人群中存活。这就是所谓的Goldberg的积木式假设或猜想[7]。简而言之,低阶短模式通常被称为构建模块,这一假设表明,通过重组或交叉,高度变异,短期和低阶积木块逐步形成更好的解决方案。进一步的数学分析和实际意义仍然是一个积极的研究课题。
这个定理意味着,具有高于平均概率的低阶模式更有可能在群体中生存。这就是所谓的 Goldberg 积木块假设/猜想(building-block
hypothesis) [7]。简而言之,低阶、短长度的模式通常被称为积木块。这一假设表明,更好的解会通过积木块的重组或交叉以及高适应度变异,逐步形成。进一步的数学分析和实际意义仍然是一个活跃的研究课题。
尽管这个模式定理有重要结果,但它几乎没有关于遗传算法收敛速度的信息。因此,在本章其余部分中,我们简要介绍一些关于 GA 收敛的结果。
收敛性分析
关于遗传算法收敛性的研究很多,关键结果可以在几十篇理论文献中找到 [3, 10, 12, 14-16]。然而,从介绍的角度来看,在本章其余部分,我们主要介绍 Louis 和 Rawlins 的结果 [12] ,他们的结果为遗传算法的主要特征提供了一些很好的见解。
在我们继续之前,让我们介绍一下汉明距离(Hamming distance)的基本概念,它是两个等长的串之间的距离度量。实质上,汉明距离是两个字符串中相应字符不同的符号或位置的数量。换句话说,如果从一个字符串开始,那么需要更换为另一个字符串的替换或替换的最小数量。例如,theory 和 memory 之间的汉明距离是 3,因为只有前三个字符是不同的。1234567 和 1122117 之间的汉明距离是 5。
Louis 和 Rawlins 的主要成果可以总结如下。对于 $n$ 个二进制字符串的集合,每个字符串的固定长度为 $m$ 且有 $n(n-1)/2$ 对样本。平均汉明距离可以用均值为 $H_0$、标准差为 $\sigma_0$ 的正态分布来估计。即,
$$H_0 = \frac m2, \quad \sigma_0 = \frac {\sqrt m}{2} \tag 8$$
传统的单点交叉随机配对不会改变平均汉明距离。
在包含比例为 $p_j$ 的二进制等位基因 $j$ 的群体中,可以用二项式分布来近似下一代中产生等位基因 $j$ 的 $k$ 个副本的概率
$${n \choose k} p_j^k (1 - p_j) ^{(n - k)} \tag 9$$
原则上,可以估计等位基因出现的特定频率的概率,但数学分析是复杂的。对于当前目的,在 $t$ 代等位基因频率取值 $p$ 的概率 $A(p, t)$ 可以近似为
$$A(p, t) = \frac {6 p_0 (1 - p_0)}{n} \bigl ( 1 - \frac 2n\bigr)^t \tag {10}$$
其详细推导可以在 Gale [6] 中找到。
因此,在目标景观(无选择压力)下,等位基因在 $t$ 代保持固定的概率为 $P(t) = 1 - A(p, t)$。对于长度为 $m$ 的染色体,所有等位基因保持固定的概率可以通过下式估算
$$p(t, m) = \Bigl [ 1 - \frac{6 p_0 (1 - p_0)}{n} \bigl ( 1 - \frac 2n\bigr )^t \Bigr]^m \tag {11}$$
当目标函数是常数时,它为函数提供了一个上界。例如,对于 $n = 40$,具有 100 位的染色体的群体,在 100 代之后,我们有 $t = 100$、$m = 100$、$n = 40$ 以及 $p_0 = 0.5$(二元)。初始的汉明平均距离是$m/2$。因此,前面的概率变成了
$$P(t, m) = \Bigl [ 1 - \frac{6 \times 0.5 (1 - 0.5)}{40} (1 - \frac{2}{40})^{100}\Bigl]^{100} \approx 0.978 \tag {12}$$
这对应于概率的上限为 97.8%。然而,如果我们将种群规模增加到 $n = 100$(保持其他不变),那么概率$P \approx 0.819$。
值得指出的是,这个概率基本上等位基因都是固定的。换句话说,这是过早收敛的可能性。如前所述,增加种群规模可以减少这种过早收敛概率,并且大的种群规模的确存在于自然界。
其他研究提供了更多特殊的结果,这些结果在实践中可能非常有用 [1, 2, 8, 9]。例如,收敛概率为 $\xi$ 的 GA 迭代次数 $t(\xi)$ 可由下式估计
$$t(\xi) \le \biggl \lceil \frac{ln(1 - \xi)}{ ln \Bigl \{ 1 - min \bigl [ (1 - \mu)^{Ln}, \mu^{Ln} \bigr] \Bigr \} } \biggr \rceil \tag {13}$$
其中 $\mu$ = 突变率、$L$ = 字符串长度、$n$ = 种群规模。这对于单目标优化是有效的。
对于多目标优化,也有一些有趣的结果。例如,Villalobos-Arias 等人提出一个元启发式算法的转移矩阵 $P$ 有一个平稳分布 $\pi$
$$\vert P_{ij}^k - \pi_j \vert \le (1 - \xi)^{k - 1}, \quad \forall i, j, \quad (k = 1, 2, ...) \tag {14}$$
其中 $\xi$ 是变异概率 $\mu$ 、字符串长度 $L$ 和种群规模的函数。例如,$\xi = 2^{nL}\mu^{nL}$,所以 $\mu \lt 0.5$ [17]。值得指出的是,在处理多目标优化时必须小心。一些算法变体可以满足上述条件,但是它们在实践中可能并不总是收敛。这是由于一些理论结果具有严格的(几乎不现实的)假设。然而,某些精英主义的先前条件通常可以有良好的收敛性。
参考文献
[1] Aytug H, Bhattacharrya S, Koehler GJ. A Markov chain analysis of genetic algorithms with power of 2 cardinality alphabets. Euro J Operational Res 1996;96(1):195–201.
[2] Aytug H, Koehler GJ. New stopping criterion for genetic algorithms. Euro J Operational Res 2000;126(2):662–74.
[3] Eiben AE, Aarts EHL, Van Hee KM. Global convergence of genetic algorithm: a Markov chain analysis. In: Schwefel H-P, Männer R, editors. Parallel problem solving from nature. Berlin, Germany: Springer; 1991. p. 4–12.
[4] De Jong K, Analysis of the behavior of a class of genetic adaptive systems, Ph.D. thesis, University of Michigan, Ann Arbor, MI, USA; 1975.
[5] Fogel DB. Evolutionary computation: toward a new philosophy of machine intelligence. 3rd ed. Piscataway, NJ.: IEEE Press; 2006.
[6] Gale JS. Theoretical population genetics. London, UK: Unwin Hyman Ltd; 1990.
[7] Goldberg DE. Genetic algorithms in search, optimisation and machine learning. Reading, MA, USA: Addison-Wesley; 1989.
[8] Greenhalgh D, Marshal S. Convergence criteria for genetic algorithms. SIAM J Comput 2000;30(1):269–82.
[9] Gutjahr WJ. Convergence analysis of metaheuristics. Anna Inf Sys 2010;10(1):159–87.
[10] He J, Kang LS. On the convergence rates of genetic algorithms. Theor Comput Sci 1999;229(1):23–9.
[11] Holland J. Adaptation in natural and artificial systems. Ann Arbor, MI, USA: University of Michigan Press; 1975.
[12] Louis SJ, Rawlins GJE. Predicting convergence time for genetic algorithms. In: Whitley LD, editor. Foundations of genetic algorithms, vol. 2. Los Altos, CA, USA: Morgan Kaufman;1993. p. 141–61.
[13] Michalewicz Z. Genetic algorithms + data structures = evolution programs. SpringerVerlag; 1999.
[14] Rudolph G. Convergence analysis of canonical genetic algorithms. IEEE Trans Neural Netw 1994;5(1):96–101.
[15] Sharapov RR. Genetic algorithms: basic ideas, variants and analysis. In: Obinata G, Dutta A, editors. Vision systems: segmentation and pattern recognition. Vienna, Austria: I-Tech; June 2007.
[16] Suzuki J. A Markov chain analysis on simple genetic algorithms. IEEE Trans Sys Man Cybern 1995;25(4):655–9.
[17] Villalobos-Arias M, Coello CAC, Hernández-Lerma O. Asymptotic convergence of metaheuristics for multiobjective optimization problems. Soft Comput 2005;10(11):1001–5.