萤火虫算法

发表于 2018-06-12 更新于 2022-11-09 分类于 Algorithm 阅读次数：

自然启发式的元启发式算法，特别是基于群体智能的，在过去的 10 年中备受关注。萤火虫算法（firefly algorithm，FA）出现于 2008 年，相关文献随着应用的不断扩大而显著扩大。在本章中，我们首先介绍标准萤火虫算法，然后简要回顾一下变体。我们还分析了 FA 的特点，并试图回答 FA 为什么如此有效的问题。

萤火虫算法

FA 由 Xin-She Yang 于 2007 年底开发并于 2008 年发表 [48, 49]。 FA 基于萤火虫的闪烁模式和行为。因此，让我们首先描述热带萤火虫的闪烁行为。

萤火虫行为

在热带和温带地区，夏季天空中，萤火虫的闪烁是一个惊人的景象。大约有 2000 种不同的萤火虫，大多数萤火虫会产生短而有节奏的闪烁。对于特定某种萤火虫而言，其闪烁模式通常是独特的。闪烁由生物发光过程产生；这种信号系统的真正功能仍在争论中。然而可以确定，这种闪烁发光的两个基本功能是吸引交配伙伴（交流）并吸引潜在的猎物 [32]。此外，闪光也可以作为一种保护性的警告机制，提醒潜在的捕食者萤火虫的苦味。

有节奏的闪光、闪光的速度以及两次闪光之间的时间量构成了将两性聚集在一起的信号系统的一部分 [32]。雌性对同一物种中雄性特有的闪光模式作出应答，而在 Photuris 等物种中，雌性萤火虫可以偷听（eavesdrop）生物发光的求偶信号，甚至模仿其他物种的交配闪光模式，以引诱和吃掉误以为闪光是潜在合适配偶的雄性萤火虫。一些热带萤火虫甚至可以同步它们的闪光，从而形成新兴的生物自组织行为。

我们知道，在距光源特定距离 $r$ 处的光强服从平方反比定律。也就是说，光强 $I$ 随机距离 $r$ 以 $I \propto 1/r^2$ 增强。此外，空气吸收光，随着距离的增加，光变得越来越弱。这两个因素结合在一起，使得大多数萤火虫在一个有限的距离能够被发现，在夜间通常是几百米，足以让萤火虫交流。

闪光可以通过与待优化的目标函数相关联的方式进行表达，从而可以制定新的优化算法。

标准萤火虫算法

现在我们可以理想化一些萤火虫的闪烁特性，从而开发出萤火虫启发（firefly-inspired）算法。为了简化描述标准 FA，我们现在使用以下三个理想化规则：

所有的信息都是无性别的，所以不论性别如何，一个萤火虫都会被其他萤火虫吸引。
吸引力与光线的亮度成正比。因此，对于任何两个萤火虫，发光较暗的将朝向发光较亮的。吸引力与亮度成正比，两者都随距离的增加而减小。如果没有比特定萤火虫更亮的萤火虫，它会随机移动。
萤火虫的亮度受目标函数的景观影响或由目标函数景观确定。

对于最大化问题，亮度可以简单地与目标函数的值成比例。其他形式的亮度可以用类似于遗传算法中的适应度函数的方式来定义。

根据这三条规则，FA 的基本步骤可以概括为下图所示的伪代码。

光强与吸引力的变化

在萤火虫算法中，有两个重要问题：光强的变化和吸引力的表述。为了简单起见，我们总是可以假设光的吸引力取决于光的亮度，而光线的亮度又与编码后的目标函数有关。

对于最大化问题，最简单的情况是，特定位置 $x$ 处光的亮度 $I$ 可以选择为 $I(x) \propto f(x)$ 。然而，吸引力 $\beta$ 是相对的，应该在旁观者的眼中看到或者由其他萤火虫来判断。因此，它将随着萤火虫 $i$ 和萤火虫 $j$ 之间的距离 $r_{ij}$ 而变化。另外，光强随着光源的距离而减小，光也会被介质吸收，因此我们应该允许吸引力随吸收程度而变化。

在最简单的形式中，光强 $I(r)$ 根据平方反比定律变化，

$$I(r) = \frac {I_s}{r^2} \tag 1$$

其中 $I_s$ 是光源处的强度。对于具有固定的光吸收系数 $\gamma$ 的给定介质，光强 $I$ 随距离 $r$ 而变化。即，

$$I = I_0 e ^{-\gamma r} \tag 2$$

其中 $I_0$ 是在零距离 $r = 0$ 处的原始光强度。为了避免表达式 $I_s / r^2$ 在 $r = 0$ 处的奇异性，平方反比定律和吸收效应的组合效果可近似为以下高斯形式：

$$I(r) = I_0 e^{-\gamma r^2} \tag 3$$

由于萤火虫的吸引力与相邻萤火虫所看到的光强成正比，所以我们现在可以定义萤火虫的吸引力 $\beta$ 为

$$\beta = \beta_0 e ^{-\gamma r^2} \tag 4$$

其中 $\beta_0$ 是 $r = 0$ 处的吸引力。由于计算 $1/(1+r)$ 通常比计算指数函数更快，所以如果需要，该函数可以方便地近似为

$$\beta = \frac {\beta_0}{1 + \gamma r^2} \tag 5$$

在某些应用中使用这种近似可能是有利的。4 和 5 都定义了特征距离 $\Gamma = 1 / \sqrt{\gamma}$ ，在此距离上，对于式 4 而言，吸引力从 $\beta_0$ 显著变化到 $\beta_0e^{-1}$ ；对于式 5 而言，吸引力从 $\beta_0$ 变化到 $\beta_0/2$ 。

在实际实现中，吸引力函数 $\beta(r)$ 可以是任何单调减函数，如下面的一般形式：

$$\beta(r) = \beta_0 e ^{-\gamma r^m}, \quad (m \ge 1) \tag 6$$

对于固定的 $\gamma$ ，特征长度变为

$$\Gamma = \gamma^{-1/m} \to 1, \quad m \to \infty \tag 7$$

相反，在优化问题中，对于给定长度 $\Gamma$ ，参数 $\gamma$ 可以用作典型的初始值。即，

$$\gamma = \frac {1}{\Gamma ^ m}, \tag 8$$

对于分别在 $x_i$ 和 $x_j$ 处的萤火虫 $i$ 和萤火虫 $j$ 之间的笛卡尔距离为

$$r_{ij} = \Vert x_i - x_j \Vert = \sqrt{ \sum_{k=1}^d (x_{i,k} - x_{j, k})^2} \tag 9$$

其中 $x_{i, k}$ 是第 $i$ 只萤火虫的空间坐标 $x_i$ 的第 $k$ 个分量。在 2D 情况下，我们有

$$r_{ij} = \sqrt{(x_i - x_j)^2 + (y_i - y_j)^2} \tag {10}$$

萤火虫 $i$ 被其他更具吸引力的（更亮的）萤火虫 $j$ 吸引的移动行为，可以由下式确定

$$x_i^{t+1} = x_i^t + \beta_0 e ^{ - \gamma r_{ij}^2} (x_j^t - x_i^t) + \alpha \epsilon_i^t \tag {11}$$

其中第二项是由于吸引力。第三项是随机化，其中 $\alpha$ 是随机化参数， $\epsilon_i$ 是服从高斯分布或均匀分布的随机向量。例如，最简单的形式是 $\epsilon_i$ 可以用 rand - 1/2 代替，其中 rand 是一个随机数生成器，服从在 [0, 1] 范围的均匀分布。对于大部分实现而言，我们可以取 $\beta_0 = 1$ 和 $\alpha \in [0, 1]$ 。

受控随机化

算法收敛性的进一步改进是改变随机化参数 $\alpha$ ，使其随着最佳逼近逐渐减小。例如，我们可以使用

$$\alpha = \alpha_{\infty} + (\alpha_0 - \alpha_{\infty}) e^ {-t} \tag {12}$$

其中 $t \in [0, t_{max}]$ 是模拟的伪时间， $t_{max}$ 是最大代数。 $\alpha_0$ 是初始随机化参数，而 $\alpha_{\infty}$ 是终值。我们也可以使用与几何退火制度类似的函数。即，

$$\alpha = \alpha_0 \theta^t \tag {13}$$

其中 $\theta \in (0, 1]$ 是随机下降常数，在大多数应用中，我们可以使用 $\theta = 0.95 \sim 0.99$ 和 $\alpha_0 = 1$ 。

另外，在当前版本的 FA 算法中，我们没有明确地使用当前的全局最优 $g_*$ ，尽管我们只是用它来解码最终的最佳解。我们的模拟表明，如果我们在更新公式 11 中增加一个额外项 $\lambda \epsilon_i (g_* - x_i)$ ，效率可能会提高。这里 $\lambda$ 是一个类似于 $\alpha$ 和 $\beta$ 的参数， $\epsilon_i$ 是随机向量。这些可能成为进一步研究的重要主题。

值得指出的是，公式 11 是偏向更亮萤火虫的随机游走。如果 $\beta_0 = 0$ ，它就变成一个简单随机游走。此外，随机化术语可以很容易地扩展到其他分布，例如 Lévy 飞行。

参数 $\gamma$ 表征吸引力的变化，其值对于确定收敛速度以及 FA 算法的行为非常重要。理论上， $\gamma \in [0, \infty)$ ，但实际上， $\gamma = O(1)$ 由待优化系统的特征长度 $\Gamma$ 决定。因此，对于大多数应用，它通常在 0.001 到 1000 之间变化。

算法分析

现在我们来仔细看看萤火虫算法并分析它的关键特性。

规模与极限

值得指出的是，上一节中定义的距离 $r$ 不限于欧几里得距离。根据感兴趣的问题类型，我们可以定义 d-维空间中的其他距离 $r$ 。例如，对于作业调度问题， $r$ 可以被定义为时滞或时间间隔。对于复杂网络，如互联网和社交网络，距离 $r$ 可以定义为局部聚类程度与顶点平均接近度的组合。事实上，优化问题中任何可以有效表征的感兴趣量的度量都可以当作“距离” $r$ 。

典型的规模 $\Gamma$ 应该与我们优化问题中涉及的规模相关联。如果 $\Gamma$ 是一个给定的优化问题的典型规模，对于大量的萤火虫，即， $n \gg k$ ，其中 $k$ 是局部最优的数量，那么这些 $n$ 个萤火虫的初始位置应该是在整个搜索空间中相对均匀的分布。随着迭代的进行，这些萤火虫将会收敛到所有局部最优（包括全局最优）。通过比较所有这些最优解中的最佳解，可以很容易地达到全局最优解。我们最近的研究表明，有可能证明当 $n \to \infty$ 和 $t \gg 1$ 时，萤火虫算法将接近全局最优解。实际上，正如本章后面所展示的那样，它会很快收敛。

当 $\gamma \to 0$ 和 $\gamma \to \infty$ 时，有两个重要的极限或渐近情况。对于 $\gamma \to 0$ ，吸引力是恒定的 $\beta = \beta_0$ 且 $\Gamma \to \infty$ 。这相当于说，对于理想化的夜空，光强不会降低。因此，在这里萤火虫能够看见所有地方的闪烁。因此，可以很容易地达到（通常是全局的）最佳值。如果我们删除原始算法伪代码图中 $j$ 的内部循环，并将 $x_j$ 替换为当前的全局最优 $g_*$ ，那么 FA 退化为 APSO 的特例。这种特殊情况的算法效率与 PSO 相同。

另一方面，极限情况 $\gamma \to \infty$ 导致 $\Gamma \to 0$ 且 $\beta(r) \to \delta(r)$ ，这是迪拉克三角函数（Dirac delta function），也就是说，在其他萤火虫眼中，吸引力几乎为零。这相当于萤火虫随机漫步在非常厚的雾区。没有其他的萤火虫可以看到，每只萤火虫都以完全随机的方式游走，这就变成了模拟退火（SA）。

因为萤火虫算法通常是在这两种极端之间的情况，所以可以调整参数 $\gamma$ 和 $\alpha$ ，使其可以胜过 SA 和 PSO。事实上，FA 可以同时有效地发现全局最优和局部最优。这个优点将在后面的实现中详细说明。

FA 的另一个优势是不同的萤火虫几乎可以独立工作。因此它特别适用于并行化的实现。它甚至比遗传算法和 PSO 更好，因为萤火虫围绕每个最佳聚集地更密集。

吸引与扩散

以光强的吸引力为开发机制的新理念最早是 Xin-She Yang 在 2007 年和 2008 年的萤火虫算法（FA）中使用的。在 FA 中，吸引力（和光强）与光强的平方反比变化规律以及吸收系数相关联。因此，我们有一个新的项 $\beta_0 exp [-\gamma r^2]$ ，其中 $\beta_0$ 是在距离 $r = 0$ 处的吸引力， $\gamma \gt 0$ 是吸收系数 [48]。

这种吸引力的主要功能是使算法快速收敛，因为这些多智能体系统进化、交互和吸引，会产生一些自组织行为和吸引子。随着群代理的演化，它们的吸引子状态有可能走向真正的全局最优。

这种新颖的吸引机制是自然启发计算和计算智能文献中的第一种。这种机制也激励他人设计类似或其他类型的吸引机制。其他算法也使用来源于自然界的平方反比定律。例如，电荷系统搜索（charged
system search，CSS）使用库仑定律；引力搜索算法（gravitational search algorithm，GSA）使用牛顿引力定律。

无论是什么吸引机制，从元启发式的角度来看，基本原则是一样的：也就是说，它们允许群代理相互作用，并提供一个强制项来指导种群的收敛。

吸引力主要提供了用于开发的机制，但是，通过适当的随机化，还可以进行一定程度的探索。然而，在随机游走和扩散随机化的框架下可以对探索进行更好的分析。从马尔可夫链的角度来看，随机行走和扩散都是马尔可夫链。事实上，布朗扩散，如墨滴在水中的散布，是随机游走的。代理或解 $x_i$ 的最基本的随机游走可以写成如下形式：

$$x_i^{(t+1)} = x_i^{(t)} + \epsilon \tag {14}$$

其中 $t$ 是步骤计数器。这里 $\epsilon$ 是服从零均值的正态分布的随机数。这给出了一个粒子或代理的平均扩散距离，它是有限步长 $t$ 的平方根。也就是说，距离是 $\sqrt{Dt}$ 的阶数，其中 $D$ 是扩散系数。更具体地说，在 d-维情况下的随机游走的方差可以写成

$$\sigma^2(t) = \vert v_0 \vert ^2 t^2 + (2dD)t \tag {15}$$

其中 $v_0$ 在这里是可以被视为零的漂移速度。

这意味着如果 $t$ 足够大，可以覆盖整个搜索域。因此，布朗运动 $B(t)$ 中的步长实质上是服从零均值和时间相关方差的高斯分布。扩散过程可以看作是服从高斯分布的一系列布朗运动。由于这个原因，标准扩散通常被称为高斯扩散。如果每一步的运动不是高斯的，那么扩散称为非高斯扩散。另一方面，随机行走可以采取多种形式。如果步长服从其他分布，我们必须处理更广义的随机行走。一种非常特殊的情况是当步长服从 Lévy 分布，这种随机游走被称为 Lévy 飞行或 Lévy 行走。

值得指出的是，最初的萤火虫算法是为了与 Lévy 飞行相结合而开发的，其性能良好 [49]。

FA 的特例

FA在很多方面确实很丰富。首先，它利用吸引力来影响群体的行为。由于局部吸引力往往比长距离吸引力更强，因此 FA 中的群体可以自动细分为多个小组（取决于问题的形式）这使得 FA 能够自然地处理多峰、非线性优化问题。

此外，如果我们仔细看一下更新公式 11，这个非线性方程提供了更丰富的特性。首先，如果 $\gamma$ 非常大，那么吸引力或光强会下降得很快。这意味着 11 中的第二项变得可以忽略不计，就产生了标准 SA。其次，如果 $\gamma$ 非常小（即 $\gamma \to 0$ ），则指数因子 $exp [- \gamma r_{ij}^2] \to 1$ 。我们有

$$x_i^{t+1} = x_i^t + \beta_0 (x_j^t - x_i^t) + \alpha \epsilon_i^t \tag {16}$$

如果我们进一步设 $\alpha = 0$ ，方程 16 变成差分进化的变体。

另一方面，如果我们用目前的全局最佳解 $g_*$ 代替 $x_i^t$ ，我们就有

$$x_i^{t+1} = x_i^t + \beta_0 (g_* - x_i^t) + \alpha \epsilon_i^t \tag {17}$$

这实质上是 2008 年由 Xin-She Yang 引入的 APSO [48]。

第三，我们设 $\beta_0 = 0$ 并让它与 $x_i$ 相关，那么 16 变成和声搜索（harmony search，HS）中的音高（pitch）调整变体。

因此，我们基本上可以说 DE、APSO、SA 和 HS 是 FA 的特例。相反，在一定程度上，FA 可以被认为是所有四种算法（DE、APSO、SA 和 HS）的良好组合。此外，FA 使用非线性更新方程，与标准 PSO 和 DE 中使用的线性更新方程相比，可产生更丰富的行为和更高的收敛性。因此，在许多应用中，如多峰优化、分类、图像处理和特征选择等，FA 可以超越其他算法，这一点也不令人惊讶，我们将在后面的应用中看到。

实现

在 Mathworks file exchange 网站上可以找到没有 Lévy 飞行的 FA 实现 demo 版。在此实现中，参数值为 $\alpha_0 = 0.5$ 、 $\gamma = 1$ 和 $\beta_0 = 1$ 。显然，可以调整这些参数以适应不同尺度下的各种问题。

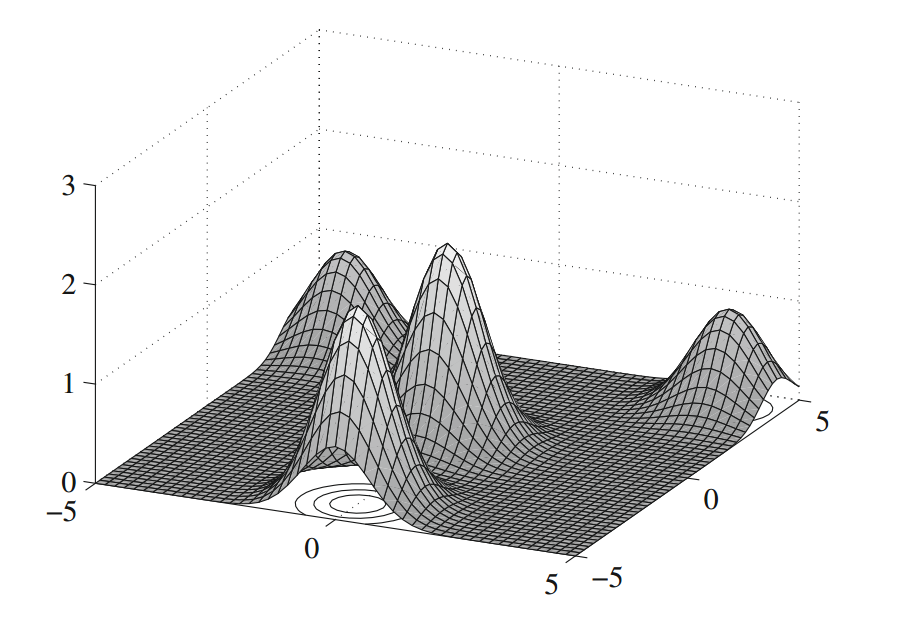
为了演示 FA 如何工作，我们使用四峰函数的简单示例

$$f(x, y) = e^{- (x-4)^2 - (y - 4)^2} + e^{-(x+4)^2 - (y - 4)^2} + 2 \bigl[ e^{-x^2-y^2} + e^{-x^2 - (y+4)^2} \bigr]$$

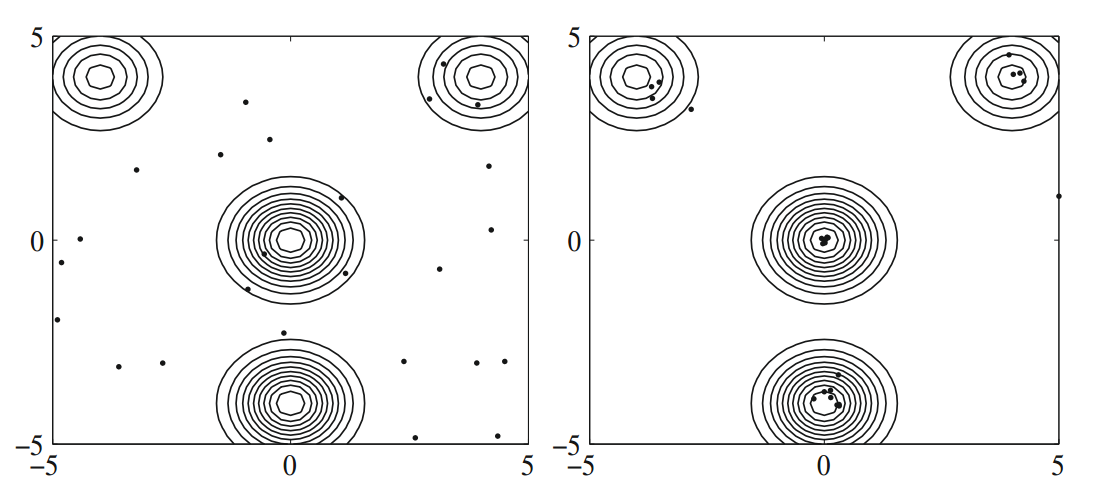
其中 $(x, y) \in [-5, 5] \times [-5, 5]$ 。如下图所示，该函数有四个峰值，两个是在 $(-4, 4)$ 和 $(4, 4)$ 处 $f = 1$ 的局部峰值；两个是在 $(0, 0)$ 和 $(0, -4)$ 处 $f_{max} = 2$ 的全局峰值。

我们可以看到，这四种最优都可以用 25 只萤火虫在大约 20 代找到（见下图）。所以，函数评估的总次数大约是 500 次。这比大多数现有的元启发式算法更有效率。

萤火虫算法的变种

FA 变体

标准 FA 非常有效，但仍有改进的余地。在过去几年中，研究人员尝试了各种方法来提高性能并加快算法的收敛速度。因此，已经开发了不少变体 [19, 42, 37]。但是，因为相关文献正在迅速扩大和更多变体会出现，这里不可能列出所有这些变体。本节简要概述了其中一些变体：

离散萤火虫算法（Discrete firefly algorithm，DFA）。 Sayadi 等人 [42] 将萤火虫算法扩展到处理 NP-hard 调度问题，并开发了一个强大的离散版 FA。他们的结果显示 DFA 可以胜过现有的算法，如 ACO。同时，Durkota 独立为 QAP 问题提供了一个 DFA 的良好实现 [14]。另外，由 Hassanzadeh 等人开发的基于 FA 的图像分割方法 [24] 可以比 Otsu 法和递归 Otsu 法更有效率。另一方面，Jati 和 Suyanto 对萤火虫算法进行了离散化处理，并且证明了它在解决 NP-hard 旅行商问题（TSP）中的有效性 [29]。此外，Chandrasekaran 和 Simon 提出了一个有效的二进制实数编码的 FA 变体来研究网络和可靠性受限的机组组合问题（unit commitment problem）[9]。
混沌萤火虫算法（Chaotic firefly algorithm，CFA）。Coelho 等人在 2011 年提出了混沌 FA。该 CFA 胜过其他算法 [11, 12]。Yang 研究了 FA 在不同参数范围内的固有混沌特性，通过调整 $\beta$ 和 $\gamma$ 可以提高性能 [51]。同时，Gandomi 等人研究了不同的混沌映射并进行了广泛的性能比较，得出结论：有些混沌映射确实可以通过用这些混沌映射替换 FA 中的一些参数来提高 FA 的性能 [21]。
拉格朗日萤火虫算法（Lagrangian firefly algoirthm，LFA）。另一个有趣的变体是 Rampriya 等人提出的拉格朗日萤火虫算法。解决电力系统的机组组合问题 [41]。
模因萤火虫算法（Memetic firefly algorithm，MFA）。Fister Jr. 等人开发了一种 FA 的离散变体，称为模因萤火虫算法，用于求解组合图着色问题，并且有着令人鼓舞的结果 [18]。
多目标离散萤火虫算法（Multiobjective discrete firefly algorithm，MDFA）。Apostolopoulos 和 Vlacho 扩展了 FA，并开发了一个用于经济地排放负荷分配问题的多目标优化离散版本，并且他们的比较表明这个变体是非常有效的 [6]。同时，Arsuaga-Rios 和 Vega-Rodriguez 独立地提出了另一个多目标 FA（MOFA），用于优化工作量管理工具，以最大限度地降低网格计算中的能耗 [4]。此外，Li 和 Ye 使用 FA 来解决多目标生产调度系统 [33]。此外，Marichelvam 等人提出了一个多目标混合车间调度问题的离散 FA 变体 [35]。
多目标萤火虫算法（Mulitobjective firefly algorithm，MOFA）。 Yang 还将单目标优化的 FA 扩展到连续设计问题的多目标优化 [53]。
多目标增强萤火虫算法（Multi-objective enhanced firefly algorithm，MOEFA）。 Amiri 等人提出了一个多目标增强 FA 用于复杂网络中的社区检测 [3]。
混合萤火虫算法（Hybrid firefly algorithms，HFA）。通过将 FA 与其他算法杂交来实现许多混合算法。例如，Giannakouris 等人将 FA 与蚁群优化相结合，取得了较好的结果 [22]。Abdullah 等人将 FA 与差分进化相结合来估计非线性生物模型参数，他们的研究表明，该混合可以成为一种强大的工具，对于许多应用来说计算时间更短 [2]。Yan 等人提出了一种带自适应策略的改进 FA [55]。
有捕食者的并行萤火虫算法（Parallel firefly algorithm with predation，pFAP）。Luz 等人提出了有捕食者的 FA 并行实现并将其应用于导热逆问题 [34]。

对于离散问题和组合优化，离散形式的 FA 已经被开发出来，具有优越的性能 [42, 29, 18, 14]，可用于旅行商问题（traveling-salesman problems，TSP）、图着色（graph coloring）以及其他应用。此外，还将 FA 的扩展到了多目标优化 [6, 53]。一些研究表明混沌可以提高 FA 的性能 [11, 51]，而其他研究试图将 FA 与其他算法混合以提高其性能 [22, 26, 27, 41]。

有时可以通过稍微修改标准 FA 来进行一些改进，但将改进算法归类为新变体可能不合适。例如，Farahani 等人使用高斯分布来替代缩放因子 $\alpha$ 的均匀分布，这确实显示出一些改进 [17]。另一方面，Wang 等人向 FA 引入一个发现率，并提出了改进的 FA 用于 UCAV 路径规划 [47]，他们的结果显示修改后的 FA 确实表现更好。

如何离散化 FA？

标准 FA 最初是针对连续多峰优化问题而开发的。它也可以用来解决组合优化问题，但是，我们必须找出方法将连续变量转换为离散变量。有多种不同的方法可以完成这项任务，其中一种被广泛使用的就是所谓的 sigmoidal logistic 函数

$$S(x) = \frac{1}{1+e^{-x}} \tag {18}$$

将连续变量转换为二元变量 $S$ 。对于 $x$ ，S 形函数给出当 $x \to +\infty$ 时 $S \to 1$ ；当 $x \to - \infty$ 时 $S \to 0$ 。但是，实际上这并不容易实现，因为数值可能不会在正确的范围内变化。常用的方法是与随机数 $r$ 相结合，使用条件切换。也即，

$$(u \gt r) \to 1, \quad (u \le r) \to 0 \tag {19}$$

显然，一旦我们有 $S \in \{ 0, 1\}$ ，我们就可以将它变为 $y = 2S - 1 \in \{+1, -1 \}$ 。

$S$ 的一个有趣特性是，它的导数可以很容易地通过下式计算

$$\frac{dS}{dx} = S(1 - S) \tag {20}$$

其他方式包括符号函数和随机化技术。例如，我们可以使用 $y = \mathop{\rm sign}(x)$ 来生成 +1、0、-1。另外，一个简单的（但不一定是有效的）方法是使用 $y = \lfloor x \rfloor$ ，它是不大于 $x$ 的最大整数。另一种方法是使用 mod 函数。例如，我们可以用

$$x \leftarrow \lfloor x + k\rfloor \mathop{\rm mod} m \tag {21}$$

其中 $k$ 和 $m \gt 0$ 是整数。

另一个相关问题是如何生成新的解。一旦我们有 $S = +1$ 或 $S = -1$ ，我们可以将它们用作步长，并在不同的次数/迭代 $t$ 进行局部随机游走。即，

$$y ^{t+1} = y^t + S \tag {22}$$

但是，如果设计变量仅为二元变量，则必须对新变量进行归一化。一种方法是通过在 0 和 1 之间随机交换来达成类变异（mutation-like）操作。

对于随机化，一种方法是使用与离散集相关的随机数。如果搜索空间是离散的且设计变量 $z$ 仅取有限集上的值，则可以生成随机数 $u$ （通常是均匀分布）映射到集合的基数。一旦生成随机数，就可以使用相应的有限集的值。

另一方面，两个关键问题是如何定义离散 FA 中的距离和邻域。对于诸如调度等许多组合问题，距离不是物理距离。因此，应小心谨慎地定义距离度量。可以使用任何合理的度量标准，例如时延、时间差、汉明距离、编辑距离以及 Jaccard 相似度等作为距离。

对于邻域而言，组合优化是一个更具挑战性的问题。例如，为了解决旅行商问题，邻域解可以是通过交换四个城市之间的两个链路产生的局部解，即所谓的2-opt 移动 [38]。

值得指出的是，定义邻域解的方式会显著影响任何自然启发算法的实现或变体的整体性能。这是离散元启发式算法构成当前研究活动重要组成部分的原因之一。

应用中的 FA

FA 已经引起了很多关注，并已被用于许多应用 [6, 10, 24, 42, 50, 25, 26]。自从 2008 年 Yang 的首次发表以来，已经有超过 810 篇关于 FA 的文献。正如我们所看到的，文献已经大大扩展，因此不可能在这里评述全部 800 篇论文。因此，我们仅抽取这些文献的一小部分。我们的选择可能有偏差，尽管我们打算以无偏的方式选择这些代表。

Horng 等人证明基于萤火虫的算法在数字图像压缩上使用最少的计算时间 [25, 26]。而 Zhang 和 Wu 使用 FA 来研究图像配准 [58]。 Banati 和 Bajaj 使用 FA 来进行特征选择，并表明 FA 的性能比其他算法在时间和最优性方面更好 [7]。

在工程设计问题上，Gandomi 等人 [20] 以及 Azad 和 Azad [5] 确认 FA 可以有效地解决高度非线性、多峰设计问题。 Basu 和 Mahanti [8] 以及 Chatterjee 等人在天线设计优化中应用 FA，并表明 FA 可以胜过 ABC [10]。另外，Zaman 和 Matin 还发现 FA 可以胜过 PSO 并获得全局最优解 [57]。此外，FA 已被用于为决策者生成多种选择的备选方案 [28]。

Sayadi 等人开发了一种可以有效解决 NP-hard 调度问题的 FA 的离散版本 [42]，而详细的分析已经证明了 FA 在广泛的测试问题上的效率，包括多目标负荷分配问题 [6, 49, 52]。例如，Yang 等人利用 FA 解决了考虑阀点效应非凸经济分配问题，并取得了比其他方法更好的结果 [54]。同样，Swarnkar 使用 FA 解决了经济负荷分配问题，降低了功率损耗 [45]。

此外，FA 可以用一种有效的方式解决调度和旅行商问题 [39, 29, 56]。Jati 和 Suyanto 通过离散 FA 解决了著名的旅行商问题，而 Yousif 等人使用 FA 解决网格计算中的作业调度 [56]。两项研究都表明 FA 非常有效。

对于排队系统，FA 已经被发现非常有效，正如 Kwiecia’n 和 Filipowicz 详细研究的结果 [31]。另外，对于混合整数规划和负荷分配问题，FA 也被认为非常有效 [9, 54]。

分类与聚类是 FA 性能卓越的另一个重要应用领域 [43, 40]。例如，Senthilnath 等人通过将 FA 与 11 种不同的算法进行比较提供了广泛的性能研究，并得出结论 FA 可以有效地用于聚类 [43]。在大多数情况下，FA 优于所有其他 11 种算法。 Tang 等人提供了对自然启发聚类算法的全面综述 [46]。此外，FA 已被用于训练神经网络 [36]。

对于动态环境中的优化，如 Farahani 等人 [15, 16] 和 Abshouri 等人 [1] 的研究所示，FA 也可以非常有效。

另一方面，Dutta 等人表明 FA 可以有效地解决等谱系弹簧质量系统 [13]。 Kazem 等人提出了基于混沌的 FA 与支持向量回归的股市价格预测 [30]。Grewal 等人提出了使用 FA 进行天线故障校正（antenna failure correction）的研究，并且表明 FA 非常灵活和有效 [23]。

在软件测试中，Srivastava 等人表明 FA 可以被修改以有效地生成独立的测试序列并且实现优越的性能 [44]。

为什么 FA 高效？

随着有关 FA 的文献扩展并出现新的变体，所有人都指出 FA 可以超越许多其他算法。现在我们可以自然地问：“它为什么如此高效？”要回答这个问题，让我们简单地从不同的角度分析 FA。

FA 是基于群体智能的，因此它具有与其他基于群集智能的算法相似的优点。然而，与其他算法相比，FA 有两个主要优势：自动细分和处理多峰的能力。首先，F 基于吸引力的。这导致了一个事实，即整个群体可以自动细分为多个小组，每个小组可以围绕某个峰值或局部最优。在所有这些峰值中，可找到全局最佳的解。其次，如果种群规模远高于峰值的数量，这个细分允许萤火虫能够同时找到所有最优解。在数学上， $1 / \sqrt{\gamma}$ 控制相邻组能够看见另一组萤火虫的距离。因此，整个群体可以细分为具有给定平均距离的子群体。在 $\gamma = 0$ 的极端情况下，整个群体不会再细分。

这种自动细分能力使 FA 特别适用于高度非线性、多峰优化问题。另外，可以调整 FA 中的参数使得能够随着迭代的进行来控制随机性，因此可以通过调整这些参数来加速收敛。这些优势使 FA 能够处理连续问题、聚类和分类以及组合优化。

例如，让我们使用两个函数来演示由 FA 节省的计算成本。有关详情，请参阅 Yang [49] 中更广泛的研究。对于 $d = 256$ 的 De Jong 函数，

$$f(x) = \sum_{i=1}^{256} x_i^2 \tag {23}$$

遗传算法需要 $25412 \pm 1237$ 次评估才能获得精度为 $10^{-5}$ 的最优解，而 PSO 需要 $17040 \pm 1123$ 次评估。对于 FA，我们通过 $5657 \pm 730$ 次函数评估获得了相同的精度。与 GA 和 PSO 相比，节省的计算成本分别约为 78％和 67％。

对于 Yang 森林函数

$$f(x) = \biggl ( \sum_{i=1}^d \vert x_i \vert \biggr ) \mathop{\rm exp} \biggl ( - \sum_{i=1}^d \sin (x_i^2) \biggr ), \quad -2\pi \le x_i \le 2\pi \tag {24}$$

对于 $d = 16$ ，GA 需要 $37079 \pm 8920$ ，成功率为 88%。PSO 需要 $19725 \pm 3204$ ，成功率为 98％。FA 仅需要 $5152 \pm 2493$ ，成功率为 100%。与 GA 和 PSO 相比，FA 在整体计算上分别节省了 86％和 74％。

总之，FA 有三个明显的优势：

将整个群体自动细分为多个小组
自然的处理多峰优化的能力
解的高遍历性和多样性

所有这些优势使得 FA 独特而高效。

References

[1] Abshouri AA, Meybodi MR, Bakhtiary A. New ﬁreﬂy algorithm based on multiswarm and learning automata in dynamic environments. In: Third international conference on signal processing systems (ICSPS 2011), August 27–28, Yantai, China; 2011. p. 73–7.
[2] Abdullah A, Deris S, Anwar S, Arjunan SNV. An evolutionary ﬁreﬂy algorithm for the estimation of nonlinear biological model parameters. PLoS One 2013;8(3):e56310.
[3] Amiri B, Hossain L, Crawford JW, Wigand RT. Community detection in complex networks: Multi-objective enhanced ﬁreﬂy algorithm. Knowl Based Syst 2013;46(1):1–1.
[4] Arsuaga-Rios M, Vega-Rodriguez MA. Multi-objective ﬁreﬂy algorithm for energy optimization in grid environments. Swarm Intelligence. Lect Notes Comput Sci 2012;7461:350–1.
[5] Azad SK, Azad SK. Optimum design of structures using an improved ﬁreﬂy algorithm. Int J Optim Civil Eng 2011;1(2):327–40.
[6] Apostolopoulos T, Vlachos A. Application of the ﬁreﬂy algorithm for solving the economic emissions load dispatch problem. Int J Combin 2011[Article ID 523806].
[7] Banati H, Bajaj M. Fireﬂy-based feature selection approach. Int J Comput Sci 2011;8(2):473–80.
[8] Basu B, Mahanti GK. Fireﬂy and artiﬁcial bees colony algorithm for synthesis of scanned and broadside linear array antenna. Prog Electromagnet Res B 2011;32(1):169–90.
[9] Chandrasekaran K, Simon SP. Network and reliability constrained unit commitment problem using binary real coded ﬁreﬂy algorithm. Int J Electr Power Energy Syst 2012;42(1):921–32.
[10] Chatterjee A, Mahanti GK, Chatterjee A. Design of a fully digital controlled reconﬁgurable switched beam conconcentric ring array antenna using ﬁreﬂy and particle swarm optimization algorithm. Prog Elelectromagnet Res B 2012;36(1):113–31.
[11] Coelho LS, de Andrade Bernert DL, Mariani VC. A chaotic ﬁreﬂy algorithm applied to reliability-redundancy optimization. In: 2011 IEEE Congress on Evolutionary Computation (CEC’11); 2011. p. 517–21.
[12] Coelho LS, Mariani VC. Fireﬂy algorithm approach based on chaotic Tinkerbell map applied to multivariable PID controller tuning. Comput Math Appl 2012;64(8):2371–82.
[13] Dutta R, Ganguli R, Mani V. Exploring isospectral spring-mass systems with ﬁreﬂy algorithm. Proc R Soc A 2011;467(2135):3222–40.
[14] Durkota K. Implementation of a discrete ﬁreﬂy algorithm for the QAP problem within the sage framework, B.Sc. Thesis. Czech Technical University; 2011. http://cyber.felk.cvut.cz/research/theses/papers/189.pdf; 2013 [accessed 23.05.13].
[15] Farahani SM, Abshouri AA, Nasiri B, Meybodi MR. Some hybrid models to improve ﬁreﬂy algorithm performance. Int J Artif Intell 2012;8(S12):97–117.
[16] Farahani SM, Nasiri B, Meybodi MR. A multiswarm based ﬁreﬂy algorithm in dynamic environments. In: Third international conference on signal processing systems (ICSPS 2011), August 27–28, Yantai, China; 2011. p. 68–72.
[17] Farahani SM, Abshouri AA, Basiri B, Meybodi MR. A Gaussian ﬁreﬂy algorithm. Int J Mach Learn Comput 2011;1(5):448–53.
[18] Fister I Jr, Fister I, Brest J, Yang XS. Memetic ﬁreﬂy algorithm for combinatorial optimization. In: Filipicˇ B, Šilc J, editors. Bioinspired optimization methods and their applications (BIOMA2012), 24–25 May 2012, Bohinj, Slovenia; 2012. p. 75–86.
[19] Fister I, Fister I Jr., Yang XS, Brest J. A comprehensive review of ﬁreﬂy algorithms. Swarm Evol Comput 2013;13(1):34–46. www.sciencedirect.com/science/article/pii/ S2210650213000461.
[20] Gandomi AH, Yang XS, Alavi AH. Mixed variable structural optimization using ﬁreﬂy algorithm. Comput Struct 2011;89(23–24):2325–36.
[21] Gandomi AH, Yang XS, Talatahari S, Alavi AH. Fireﬂy algorithm with chaos. Commun Nonlinear Sci Numer Simulat 2013;18(1):89–98.
[22] Giannakouris G, Vassiliadis V, Dounias G. Experimental study on a hybrid nature-inspired algorithm for ﬁnancial portfolio optimization. In: SETN 2010, Lecture notes in artiﬁcial intelligence (LNAI 6040); 2010. p. 101–111.
[23] Grewal NS, Rattan M, Patterh MS. A linear antenna array failure correction using ﬁreﬂy algorithm. Prog Electromagnet Res 2012;27:241–54.
[24] Hassanzadeh T, Vojodi H, Moghadam AME. An image segmentation approach based on maximum variance intra-cluster method and ﬁreﬂy algorithm. In: Proceedings of the sev- enth international conference on natural computation (ICNC 2011); 2011. p. 1817–21.
[25] Horng MH, Lee YX, Lee MC, Liou RJ. Fireﬂy metaheuristic algorithm for training the radial basis function network for data classiﬁcation and disease diagnosis. In: Parpinelli R, Lopes HS, editors. Theory and new applications of swarm intelligence; 2012. p. 115–32.
[26] Horng MH. Vector quantization using the ﬁreﬂy algorithm for image compression. Expert Syst Appl 2012;39(2):1078–91.
[27] Horng MH, Liou RJ. Multilevel minimum cross-entropy threshold selection based on the ﬁreﬂy algorithm. Expert Syst Appl 2011;38(9):14805–11.
[28] Imanirad R, Yang XS, Yeomans JS. Modeling-to-generate-alternatives via the ﬁreﬂy algorithm. J Appl Oper Res 2013;5(1):14–21.
[29] Jati GK, Suyanto S. Evolutionary discrete ﬁreﬂy algorithm for traveling salesman problem. ICAIS 2011, Lecture notes in artiﬁcial intelligence (LNAI 6943) 2011; 2011:393–403.
[30] Kazem A, Shariﬁ E, Hussain FK, Saberi M, Khadeer O. Support vector regression with chaos-based ﬁreﬂy algorithm for stock market price forecasting. Appl Soft Comput 2013;13(2):947–58.
[31] Kwiecia´n J, Filipowicz B. Fireﬂy algorithm in optimization of queueing systems. Bull Pol Acad Sci Tech Sci 2012;60(2):363–8.
[32] Lewis SM, Cratsley CK. Flash signal evolution, mate choice and predation in ﬁreﬂies. Ann Rev Entomol 2008;53(2):293–321.
[33] Li HM, Ye CM. Fireﬂy algorithm on multi-objective optimization of production scheduling system. Adv Mech Eng Appl 2012;3(1):258–62.
[34] Luz EFP, Campos Velho HF, Becceneri JC. Fireﬂy algorithm with predation: a parallel implementation applied to inverse heat conduction problem. In: Proceedings of 10th world congress on computational mechanics (WCCM 2012; conference presentation); 2012.
[35] Marichelvam MK, Prabaharan T, Yang XS. A discrete ﬁreﬂy algorithm for the multi-objective hybrid ﬂowshop scheduling problems. IEEE Transl Evol Comput 2013. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=6412790.
[36] Nandy S, Sarkar PP, Das A. Analysis of nature-inspired ﬁreﬂy algorithm-based back-propagation neural network training. Int J Comput Appl 2012;43(22):8–16.
[37] Nasiri B, Meybodi MR. Speciation-based ﬁreﬂy algorithm for optimization in dynamic environments. Int J Artif Intell 2012;8(S12):118–32.
[38] Ouaarab A, Ahiod B, Yang XS. Discrete cuckoo search algorithm for the travelling salesman problem. Neural computing and applications 2013. http://link.springer.com/ article/10.1007%2Fs00521-013-1402-2.
[39] Palit S, Sinha S, Molla M, Khanra A, Kule M. A cryptanalytic attack on the knapsack cryptosystem using binary ﬁreﬂy algorithm. In: Second international conference on computer and communication technology (ICCCT), 15–17 September 2011, India; 2011. p. 428–32.
[40] Rajini A, David VK. A hybrid metaheuristic algorithm for classiﬁcation using micro array data. Int J Sci Eng Res 2012;3(2):1–9.
[41] Rampriya B, Mahadevan K, Kannan S. Unit commitment in deregulated power system using Lagrangian ﬁreﬂy algorithm. In: Proceedings of IEEE international conference on communication control and computing technologies (ICCCCT2010); 2010. p. 389–93.
[42] Sayadi MK, Ramezanian R, Ghaffari-Nasab N. A discrete ﬁreﬂy meta-heuristic with local search for makespan minimization in permutation ﬂow shop scheduling problems. Int J Ind Eng Comput 2010;1(1):1–10.
[43] Senthilnath J, Omkar SN, Mani V. Clustering using ﬁreﬂy algorithm: performance study. Swarm Evol Comput 2011;1(3):164–71.
[44] Srivastava PR, Mallikarjun B, Yang XS. Optimal test sequence generation using ﬁreﬂy algorithm. Swarm Evol Comput 2013;8(1):44–53.
[45] Swarnkar KK. Economic load dispatch problem with reduce power losses using ﬁreﬂy algorithm. J Adv Comput Sci Technol 2012;1(2):42–56.
[46] Tang R, Fong S, Yang XS, Deb S. Integrating nature-inspired optimization algorithm to K-means clustering. In: The seventh international conference on digital information man- agement (ICDIM2012), 22–24 August. Macau: IEEE Publications; 2012. p. 116–23.
[47] Wang GG, Guo LH, Duan H, Liu L, Wang HQ. A modiﬁed ﬁreﬂy algorithm for UCAV path planning. Int J Hybrid Inform Technol 2012;5(3):123–44.
[48] Yang XS. Nature-inspired metaheuristic algorithms. 1st ed. Frome, UK: Luniver Press; 2008.
[49] Yang XS. Fireﬂy algorithms for multimodal optimisation. In: Watanabe O, Zeugmann T, editors. Proceedings ﬁfth symposium on stochastic algorithms, foundations and applica- tions. Lecture notes in computer science, vol. 5792; 2009. p. 169–78.
[50] Yang XS. Fireﬂy algorithm, stochastic test functions and design optimisation. Int J Bio-Inspired Comput 2010;2(2):78–84.
[51] Yang XS. Chaos-enhanced ﬁreﬂy algorithm with automatic parameter tuning. Int J Swarm Intell Res 2012;2(4):125–36.
[52] Yang XS. Swarm-based metaheuristic algorithms and no-free-lunch theorems. In: Parpinelli R, Lopes HS, editors. Theory and new applications of swarm intelligence. Intech Open Science; 2012. p. 1–16.
[53] Yang XS. Multiobjective ﬁreﬂy algorithm for continuous optimization. Eng Comput 2013;29(2):175–84.
[54] Yang XS, Hosseini SSS, Gandomi AH. Fireﬂy algorithm for solving non-convex economic dispatch problems with valve loading effect. Appl Soft Comput 2012;12(3):1180–6.
[55] Yan X, Zhu YL, Wu JW, Chen H. An improved ﬁreﬂy algorithm with adaptive strategies. Adv Sci Lett 2012;16(1):249–54.
[56] Yousif A, Abdullah AH, Nor SM, Abdelaziz A. Scheduling jobs on grid computing using ﬁreﬂy algorithm. J Theor Appl Inform Technol 2011;33(2):155–64.
[57] Zaman MA, Matin MA. Nonuniformly spaced linear antenna array design using ﬁreﬂy algorithm. Int J Microw Sci Technol 2012;vol. 2012 [Article ID: 256759].
[58] Zhang YD, Wu LN. A novel method for rigid image registration based on ﬁreﬂy algorithm. Int J Res Rev Soft Intell Comput 2012;2(2):141–6.