Jaya 优化算法及其变体

发表于 更新于 分类于 阅读次数：

本章详细介绍了 TLBO 算法、NSTLBO 算法、Jaya 算法及其变种——自适应 Jaya、拟反向 Jaya、自适应多种群 Jaya、自适应多种群精英策略 Jaya、混沌 Jaya、多目标 Jaya 和多目标拟反向 Jaya。文中举例说明了Jaya 算法及其变体在无约束和有约束单目标和多目标优化问题中的应用。还描述了覆盖率、间距和超体积三个性能指标来评估多目标优化算法的性能。

教与学优化（TLBO）算法

Rao 等人 (2011) 开发了 TLBO 算法，该算法不需要调整任何算法相关（algorithm-specific）参数。该算法描述了两种基本的学习模式：(i) 通过教师学习（称为教师阶段）；(ii) 通过与其他学员的交流学习（称为学员阶段）。在该优化算法中，一组学员被认为是群体，而提供给学员的不同学科被认为是优化问题的不同设计变量，学员的成绩与优化问题的“适应度”值类似。在整个群体中最好的解被认为是老师。设计变量实际上是给定优化问题的目标函数中涉及的参数，最佳解是目标函数的最佳值。

TLBO 的工作分为“老师阶段”和“学员阶段”两部分。下面将解释这两个阶段的工作 (Rao 2016a)。

教师阶段

学员通过老师学习是算法的第一部分。在这个阶段，老师会根据他/她的能力，尝试增加他/她教授课程的平均成绩。在任意迭代 $i$ 中，假设有 $m$ 门课程（即设计变量）、$n$ 个学员（即种群规模，$k = 1, 2, \cdots, n$），$M_{j,i}$ 是学员在在特定课程 $j (j = 1, 2, \cdots, m)$ 中的成绩。整个学员群体，所有课程的最佳成绩 $X_{total-kbest, i}$，可以认为是最佳学员 $kbest$ 的成绩。然而，由于老师通常被认为是训练学员获得更好成绩的高度学习者，所以识别出的最好的学员也认为是老师。每门课程现有的平均成绩与每门课程教师的相应成绩之间的差异由下式给出：

$$\text{Difference_Mean} _ {j, k, i} = r_i(X_{j, kbest, i} - T_FM_{j,i}) \tag 1$$

其中 $X_{j,kbest,i}$ 是课程 $j$ 中最好学员的成绩。$T_F$ 是决定均值变化的教学因子（teaching factor），$t_i$ 是取值范围在 [0, 1] 的随机数。$T_F$ 的值可以取 1 或 2。$T_F$ 的值随机等概率取决于，

$$T_F = \mathop{ \rm round} [1 + \mathop{\rm rand} (0, 1) {2 - 1}] \tag 2$$

T_F并非 TLBO 算法的参数，其值不作为算法的输入，而是由算法使用方程 (2) 随机决定。在对许多基准函数进行了大量实验之后，得出的结论是，如果 $T_F$ 的值在 1 和 2 之间，则算法性能好。而且，如果 $T_F$ 值为 1 或 2，则发现算法性能更好，并且因此为了简化算法，建议教学因子取 1 或 2。基于 $\text{Difference_Mean}_{j, k, i}$，在教师阶段根据下式更新现有解。

$$X_{j, k, i}^{‘} = X_{j, k, i} + \text{Difference_Mean} _ {j, k, i} \tag 3$$

其中 $X_{j,k,i}^{'}$ 是 $X_{j, k, i}$ 的更新值。如果它给出更好的函数值，则被接受。教师阶段结束时所有被接受的函数值都得到保留，这些值将成为学员阶段的输入。学员阶段取决于教师阶段。

学员阶段

学员通过彼此之间的交流来增加他们的知识，是算法的第二部分。学员随机与其他学员交互以增强他/她的知识。如果其他学员比他/她拥有更多的知识，学员将学习新的东西。考虑到群体规模为 $n$，下面解释该阶段的学习现象。

随机选择两个学员 $P$ 和 $Q$，使得 $X_{total-P, i}^{'} \not = X_{total-Q,i}^{'}$（其中，$X_{total-P, i}^{'}$ 和 $X_{total-Q,i}^{'}$ 分别是在教师阶段结束时，$P$ 和 $Q$ 函数值 $X_{total-P, i}$ 和 $X_{total-Q,i}$ 的更新值。）

$$X_{j, P, i}^{‘’} = X_{j, P, i}^{‘} + r_i (X_{j, P, i}^{‘} - X_{j, Q, i}^{‘}), \quad \text{If $X_{total-P, i}^{'} \lt X_{total-Q, i}^{'}$} \tag 4$$

$$X_{j, P, i}^{‘’} = X_{j, P, i}^{‘} + r_i (X_{j, Q, i}^{‘} - X_{j, P, i}^{‘}), \quad \text{If $X_{total-Q, i}^{'} \lt X_{total-P, i}^{'}$} \tag 5$$

如果 $X_{j, P, i}^{''}$ 能提供了更好的函数值，则接受它。

公式 (4) 和 (5) 用于最小化问题。对于最大化问题，使用公式 (6) 和 (7)。

$$X_{j, P, i}^{‘’} = X_{j, P, i}^{‘} + r_i (X_{j, P, i}^{‘} - X_{j, Q, i}^{‘}), \quad \text{If $X_{total-Q, i}^{'} \lt X_{total-P, i}^{'}$} \tag 6$$

$$X_{j, P, i}^{‘’} = X_{j, P, i}^{‘} + r_i (X_{j, Q, i}^{‘} - X_{j, P, i}^{‘}), \quad \text{If $X_{total-P, i}^{'} \lt X_{total-Q, i}^{'}$} \tag 7$$

TLBO 算法的流程图如下所示。TLBO 算法的最大函数评估次数 = 2 $\times$ 种群规模 $\times$ 迭代次数。

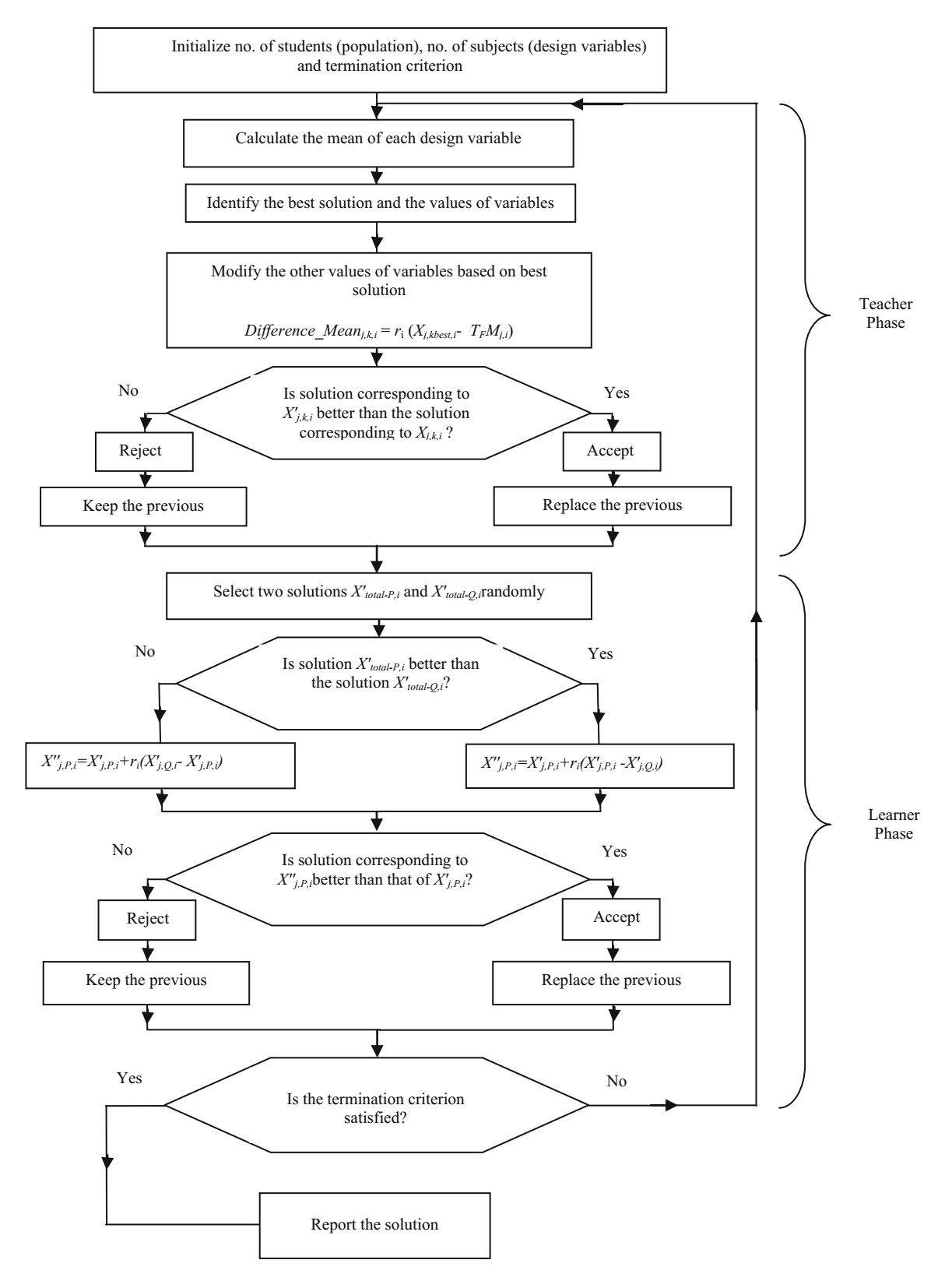
非支配排序教与学优化（NSTLBO）算法

NSTLBO 算法是为解决多目标优化问题而开发的。NSTLBO 算法是 TLBO 算法的扩展。这是一种解决多目标优化问题的后验（posteriori）方法，能够保留了多个不同的解集。NSTLBO 算法类似于 TLBO 算法，由教师阶段和学员阶段组成。为了处理多个目标，NSTLBO 算法有效地与非支配排序（non-dominated sorting）方法和拥挤距离（crowding distance）计算相结合。

开始时，初始种群随机生成 $NP$ 个解。然后依据约束支配（constraint-dominance）和非支配（non-dominance）概念对初始种群进行排序。解的优越性首先是基于约束支配概念，然后是非支配概念，然后是解的拥挤距离值。选择序（rank）最高的学员（rank = 1）作为班级的老师。如果存在不止一个具有相同秩的学员，则选择具有最高拥挤距离值的学员作为该班级的教师。这确保从搜索空间的稀疏区域（sparse phase）中选择教师。

一旦选择了教师，则依据方程 (1)-(3) 更新学员。在教师阶段之后，将更新的学员集连接到初始种群以获得 $2NP$ 的解集。这些学员依据约束支配概念、非支配概念和每个学员的拥挤距离值再次进行排秩。具有更高秩的学员被认为优于其他学员。如果两个学员的秩相同，那么具有较高拥挤距离值的学员被认为优于另一个。基于新序和拥挤距离值，选择 $NP$ 个最佳学员。这些学员根据 TLBO 算法的学员阶段进一步更新，即根据方程 (4) 和 (5) 或 (6) 和 (7)。

学员的优势性是基于学员的约束支配、非支配序和拥挤距离值来确定的。具有更高秩的学员被认为优于其他学员。如果两个学员的秩相同，那么具有较高拥挤距离值的学员被认为优于另一个。学员阶段结束后，新的学员与旧的学员结合，再次排序。基于新的排序和拥挤距离值，选择 $NP$ 个最佳学员，并且在下一次迭代的教师阶段这些学员直接更新 (Rao 2016a; Rao et al. 2016)。下图显示了 NSTLBO 算法的流程图。

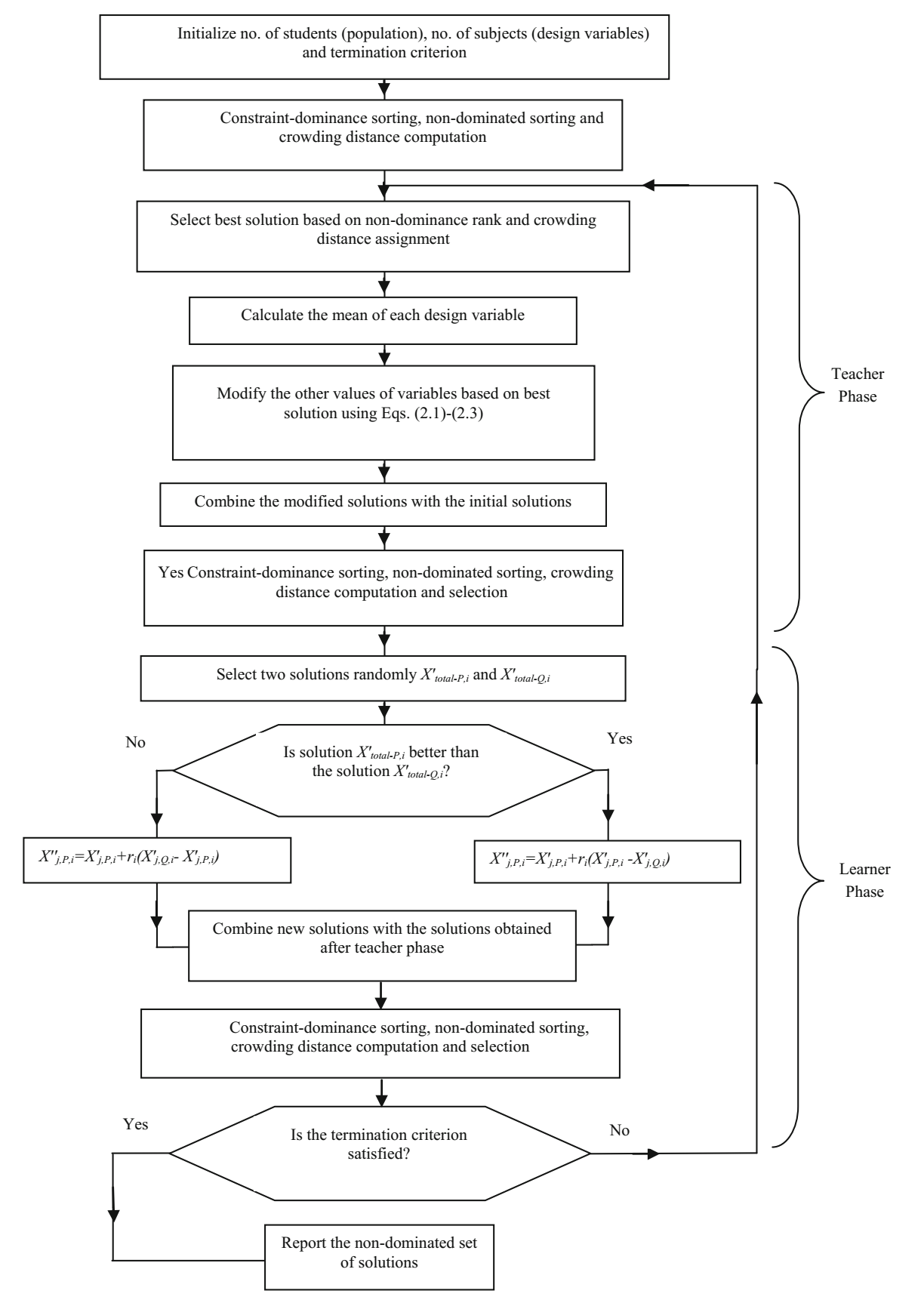
种群的非支配排序

在本方法中，基于如下支配概念将种群分为若干秩（前沿，fronts）：解 $x_i$ 被称为支配其他解 $x_j$，当且仅当解 $x_i$ 在所有目标上不比解 $x_j$ 差，且解 $x_i$ 在至少一个目标上严格比解 $x_j$ 好。如果两个条件中的任一条件不满足，则解 $x_i$ 不支配解 $x_j$。

在解集 $P$ 中，非支配解是那些不受解集 $P$ 中任一解支配的解。所有这些在第一次排序中被识别的非支配解将分配到 rank one（第一前沿， first front），并且从集合 $P$ 中删除。集合 $P$ 中剩余的解再次排序，重复该过程，直到集合 $P$ 中的所有解被排序。在约束多目标优化问题的情况下，可以使用约束支配概念。对于 NSTLBO 算法，函数评估的最大次数= 2 $\times$ 种群规模 $\times$ 迭代次数。

拥挤距离的计算

将拥挤距离分配给群体中的每个解，目的是估计围绕特定解 $i$ 的解密度。因此，沿着 $M$ 个目标的每个目标，测量解 $i$ 两侧的两个解的平均距离。该量被称为拥挤距离（$CD_i$）。可以遵循以下步骤来计算前沿 $F$ 中每个解 $i$ 的 $CD_i$。

  1. 确定前沿 $F$ 中解的数量 $l = \vert F \vert$。为集合中每个解 $i$ 分配 $CD_i = 0$。
  2. 对每个目标函数 $m = 1, 2, \cdots, M$，按 $f_m$ 的最差序对集合进行排序。
  3. 对于 $m = 1, 2, \cdots, M$，将最大拥挤距离分配给排序列表中的边界解（$CD_1 = CD_l = \infty$），对于排序列表 $j = 2$ 到 $(l - 1)$ 的所有其他解，拥挤距离如下：

$$CD_j = CD_j + \frac{f_m^{j+1} - f_m^{j - 1}}{f_m^{max} - f_m^{min}} \tag 8$$

其中 $j$ 是排序列表中的一个解，$f_m$ 是第 $m$ 个目标的目标函数值，$f_m^{max}$ 和 $f_m^{min}$ 是第 $m$ 个目标函数的最大与最小种群规模。

拥挤比较算子

基于群体中每个个体所拥有的两个重要属性，即非支配秩（$Rank_i$）和拥挤距离（$CD_i$），使用拥挤比较算子（crowding-comparison operator）比较识别两个解的优越性。因此，拥挤比较算子（$\prec_n$）可定义如下：$i \prec_n j$，如果 $(Rank_i \lt Rank_j)$ 或 $(Rank_i = Rank_j)$ 且 $(CD_i \gt CD_j)$。也就是说，在具有不同非支配秩的两个解（$i$ 和 $j$）之间，具有更低或更好秩的解是优选的。如果两个解都属于相同的前沿（$Rank_i = Rank_j$），那么位于较小拥挤区域（$CD_i \gt CD_j$）的解是优选的。

约束支配概念

如果满足以下任何一个条件，则称解 $i$ 约束支配解 $j$。解 $i$ 是可行解，而解 $j$ 不是；解 $i$ 和 $j$ 都是不可行解，但解 $i$ 有较小的总体约束冲突；解 $i$ 和 $j$ 都是可行解，解 $i$ 支配 $j$。约束支配概念保证了可行解比不可行解具有更高的秩。在可行解中，优越解（非支配解）排名高于支配解。在不可行解中，较高的秩被分配给总体约束冲突较小的解。

Jaya 算法

Rao (2016b) 开发了 Jaya 算法，该算法易于实现，不需要调整任何算法相关的参数。在 Jaya 算法中，$P$ 个初始解按照过程变量的上下界随机生成。此后，使用等式 (9) 随机更新每个解。$f$ 是要最小化（或最大化）的目标函数。有 $d$ 个设计变量。最好解对应的目标函数值为 $f\_best$，最坏解对应的目标函数值为 $f\_best$。

$$A(i+1, j, k) = A(i, j, k) + r(i, j, 1) \bigl (A (i, j, b) - \vert A(i, j, k) \vert \bigr) - r(i, j, 2) \bigl( A(i, j, w) - \vert A(i, j, k) \vert \bigr) \tag 9$$

这里 $b$ 和 $w$ 代表当前种群中最佳和最差解的索引。$i, j, k$ 是迭代、变量和候选解的索引。$A(i, j, k)$ 表示第 $i$ 次迭代中，第 $k$ 个候选解的第 $j$ 个变量。$r(i, j, 1)$ 和 $r(i, j, 2)$ 是取自 [0，1] 范围内随机数。随机数 $r(i, j, 1)$ 和 $r(i, j, 2)$ 充当缩放因子，确保算法具有良好的多样性。 Jaya 算法的主要目的是提高群体中每个候选解的适应度（目标函数值）。因此，Jaya 算法试图通过更新变量的值来将每个解的目标函数值移向最佳解。一旦变量的值被更新，更新解与相应的旧解相比较，下一代只考虑好的解（即具有更好目标函数值的解）。在Jaya 算法中，每一代解都接近最佳解，同时候选解也会远离最差解。因此，在搜索过程中达到了良好的集中性与多样性。该算法总是试图接近成功（即达到最佳解）并试图避免失败（即远离最差解）。该算法不断地努力达到最佳解以获得胜利，因此它被命名为 Jaya（在梵文中意为胜利）。

Jaya 算法的流程图如下图所示 (Rao et al. 2017)。对于每个候选解，Jaya 算法仅在每代中评估目标函数一次。因此，Jaya 算法所需的函数评估总次数 = 种群规模 $\times$ 迭代次数。

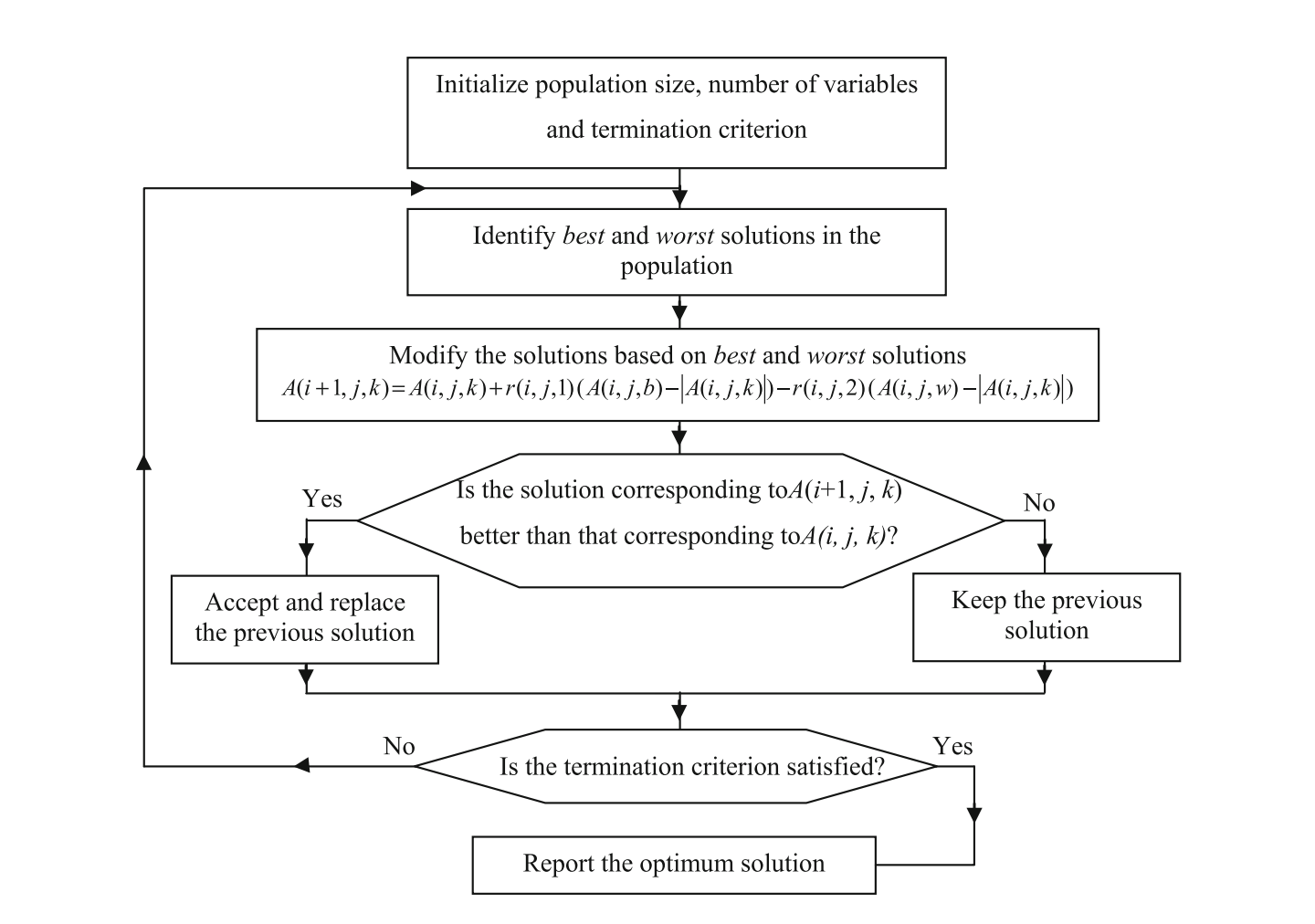
无约束优化问题的 Jaya 算法演示

为了演示 Jaya 算法，我们考虑无约束基准函数 Sphere。目标函数是找出最小化的 Sphere 函数值 $x_i$。

$$\text{minimize} ; f(x_i) = \sum_{i=1}^nx_i^2 \tag {10}$$

变量范围：$-100 \le x_i \le 100$。

该基准函数的已知解是对所有 $x_i$ 值为 0，函数值为 0。为演示 Jaya 算法，让我们假设种群规模（即候选解数量）为 5，有两个设计变量 $x_1$ 和 $x_2$ 以及 2 代为停止标准。初始种群在变量范围内随机生成，目标函数的相应值如下表所示。由于基准函数是最小化函数，$f(x)$ 的最低值被认为是最好解，$f(x)$ 的最高值被认为是最差解。

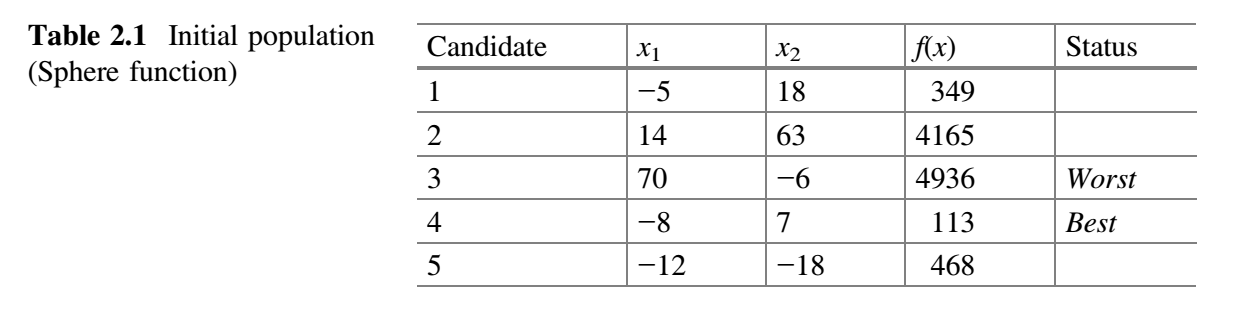
从上表可以看出，最佳解对应第四个候选解，最差解对应第三个候选解。假设 $x_1$ 对应的随机数为 $r_1 = 0.58$、$r_2 = 0.81$，$x_2$ 对应的随机数为 $r_1 = 0.92$、$r_2 = 0.49$，$x_1$ 和 $x_2$ 的新值使用公式 (9) 计算并置于下表中。例如，对于第一个候选解，第一次迭代中 $x_1$ 的新值计算过程如下：$− 5 + 0.58 ( − 8 − \vert −5 \vert ) − 0.81 (70− \vert − 5\vert ) = − 65.19$。第一次迭代中 $x_2$ 的新值计算过程如下：$18 + 0.92 (7− \vert 18 \vert ) − 0.49 (−6− \vert 18 \vert) = 19.64$。类似地，可以计算出其他候选解的 $x_1$ 和 $x_2$ 的新值。下表展示了 $x_1$ 和 $x_2$ 的新值以及相应的目标函数值。

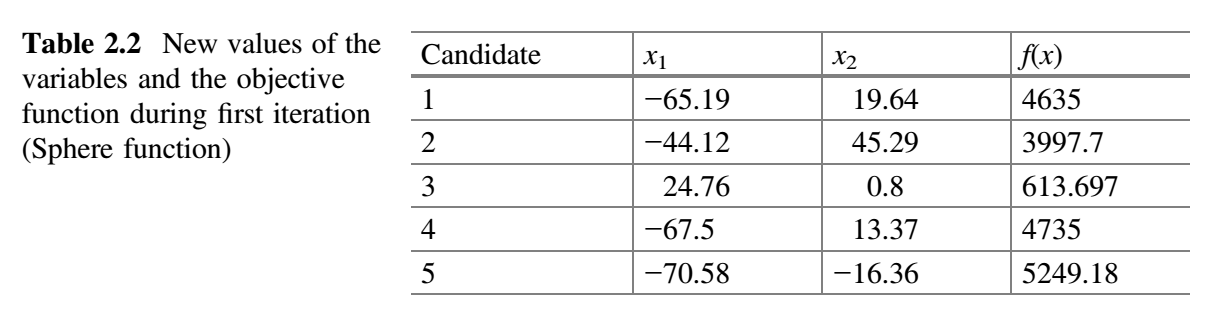
现在，比较表 2.1 和 表2.2 中的 $f(x)$ 值，将 $f(x)$ 的最佳值放在表 2.3 中。这就完成了 Jaya 算法的第一次迭代。

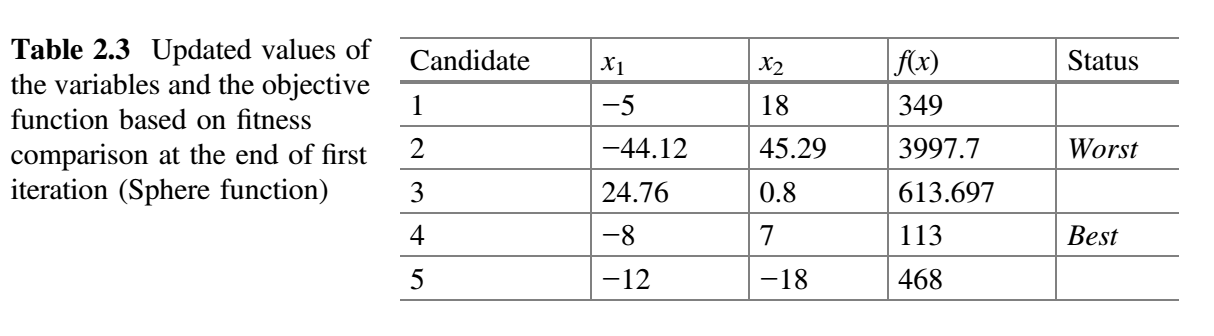
从表 2.3 可以看出，最佳解对应于第四个候选解，最差解对应于第二个候选解。在第二次迭代中，假设 $x_1$ 对应的随机数为 $r_1 = 0.27$、$r_2 = 0.23$，$x_2$ 对应的随机数为 $r_1 = 0.38$、$r_2 = 0.51$，$x_1$ 和 $x_2$ 的新值使用公式 (9) 计算。表 2.4 显示了第二次迭代中 $x_1$ 和 $x_2$ 的新值以及相应的目标函数值。现在，比较表 2.3 和 2.4 的 $f(x)$ 值，并将最佳值放在表 2.5 中。这就完成了 Jaya 算法的第二次迭代。

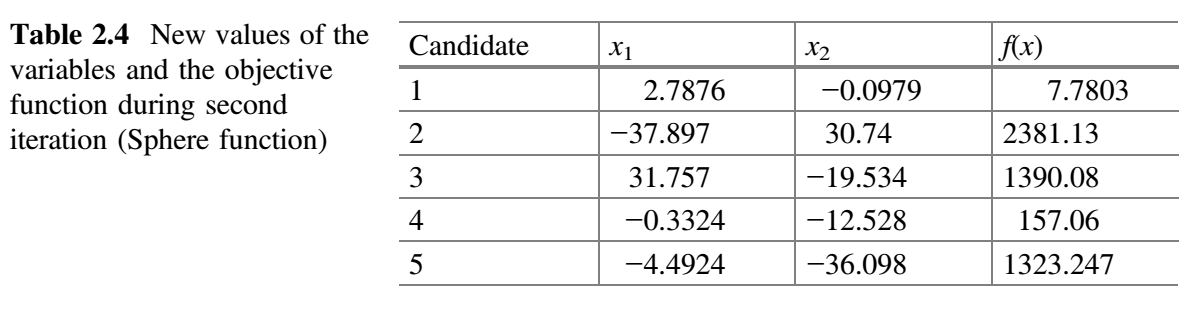
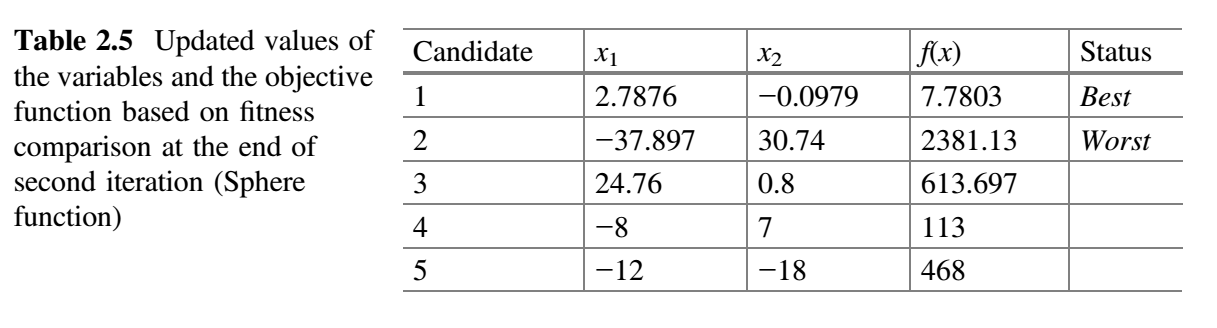
从表 2.5 可以看出，最佳解对应于第一个候选解，最差解对应于第二个候选解。还可以观察到，目标函数值在两次迭代中从 113 减小到 7.7803。如果我们增加迭代次数，那么目标函数的已知值（即 0）可以在接下来的几次迭代达到。另外，应该注意，在最大化问题情况下，最佳值意味着目标函数的最大值，并且计算将相应地进行。因此，该方法既可以处理最小化问题，也可以处理最大化问题。

为了进一步演示 Jaya 算法，考虑另一个基准函数 Rastrigin (Rao et al. 2017)。目标函数是最小化 Rastrigin 函数值 $x_i$。

$$f_{min} = \sum_{i=1}^D \bigl [ x_i^2 - 10 \cos (2\pi x_i) + 10 \bigr ] \tag {11}$$

变量取值范围：$− 5.12 \le x_i \le 5.12$。

这个基准函数的已知解对于所有 $x_i$ 为 0 函数值为 0。为演示 Jaya 算法，让我们假设种群规模为 5 (即候选解数量)，有两个设计变量 $x_1$ 和 $x_2$ 以及设 3 次迭代作为终止准则。初始种群在变量范围内随机产生，目标函数的相应值见如下表所示。

从表 2.6 可以看出，最佳解对应于第四个候选解，最差解对应于第三个候选解。现在假设 $x_1$ 对应的随机数为 $r_1 = 0.38$、$r_2 = 0.81$，$x_2$ 对应的随机数为 $r_1 = 0.92$、$r_2 = 0.49$，$x_1$ 和 $x_2$ 的新值使用公式 (9) 计算，并置于下表中。$x_1$、$x_2$ 的计算过程如下所示。

$$
\begin{align}
A_{2,1,1} & = A_{1,1,1} + r(1,1,1)\bigl ( A_{1,1,b} - \vert A_{1,1,1} \vert \bigr ) - r(1,1,2) \bigl ( A_{1, 1, w} - \vert A_{1,1,1}\vert \bigr) \
& = 0.045197073 + 0.92 (- 0.767182961 - |0.045197073|) - 0.49(-4.442417134 - |0.045197073|) \
& = - 2.856829068
\end{align}
$$

$$
\begin{align}
A_{2,2,1} & = A_{1,2,1} + r(1,2,1)\bigl ( A_{1,2,b} - \vert A_{1,2,1} \vert \bigr ) - r(1,2,2) \bigl ( A_{1, 2, w} - \vert A_{1,2,1}\vert \bigr) \
& = - 4.570261872 + 0.38(- 1.062187325 - \vert - 4.570261872\vert) - 0.81(-2.304524513 - \vert - 4.570261872\vert) \
& = - 1.142020267
\end{align}
$$

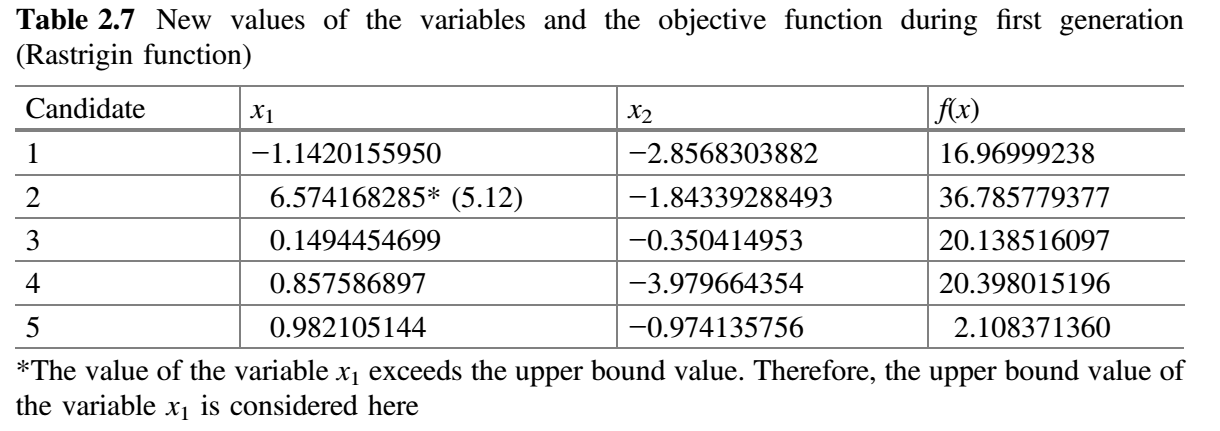
类似地，计算其他候选解的 $x_1$ 和 $x_2$ 的新值。表 2.7 显示了 $x_1$ 和 $x_2$ 的新值以及目标函数的相应值。

现在，比较表 2.6 和 2.7 的 $f(x)$ 值，并将 $f(x)$ 的最佳值放在表 2.8 中。这就完成了 Jaya 算法的第一次迭代。

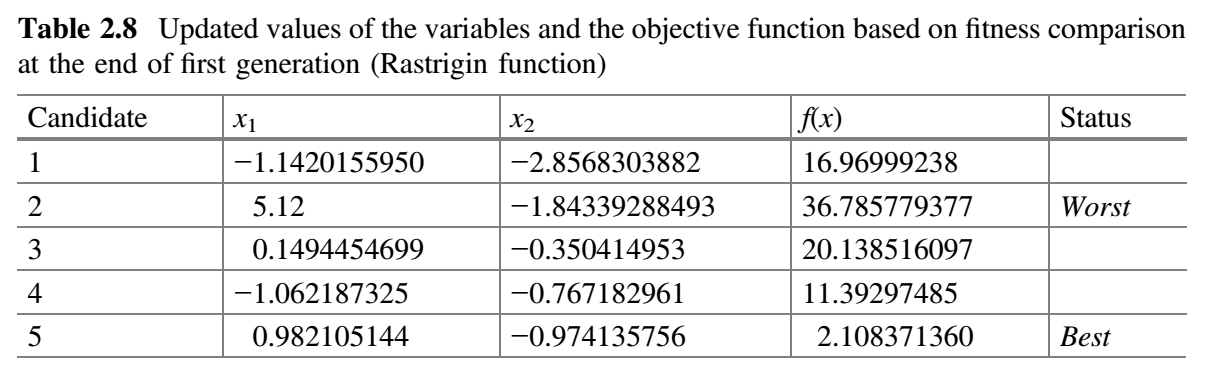
从表 2.8 可以看出，最佳解对应于第五个候选解，最差解对应于第二个候选解。在第二代中，假设 $x_1$ 对应的随机数为 $r_1 = 0.65$、$r_2 = 0.23$，$x_2$ 对应的随机数为 $r_1 = 0.38$、$r_2 = 0.51$，$x_1$ 和 $x_2$ 的新值使用公式 (9) 计算。表 2.9 显示了第二代 $x_1$ 和 $x_2$ 的新值以及目标函数的相应值。

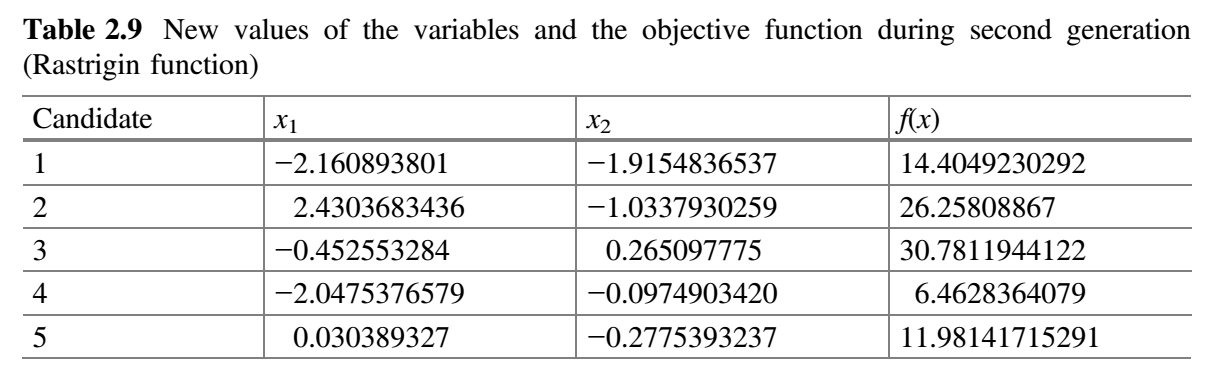
现在，比较表 2.8 和 2.9 的 $f(x)$ 值，并将最佳值放在表 2.10 中。这就完成了 Jaya 算法的第二次迭代。

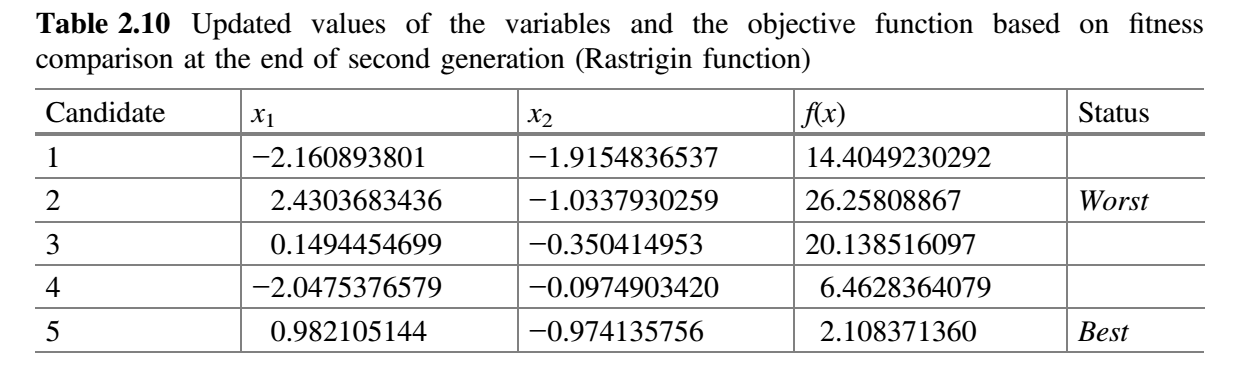
从表 2.10 可以看出，最佳解对应于第五个候选解，最差解对应于第二个候选解。在第三代中，假设 $x_1$ 对应的随机数为 $r_1 = 0.01$、$r_2 = 0.7$，$x_2$ 对应的随机数为 $r_1 = 0.02$、$r_2 = 0.5$，$x_1$ 和 $x_2$ 的变量的新值使用公式 (9) 计算。表 2.11 显示了第三代 $x_1$ 和 $x_2$ 的新值以及目标函数的相应值。

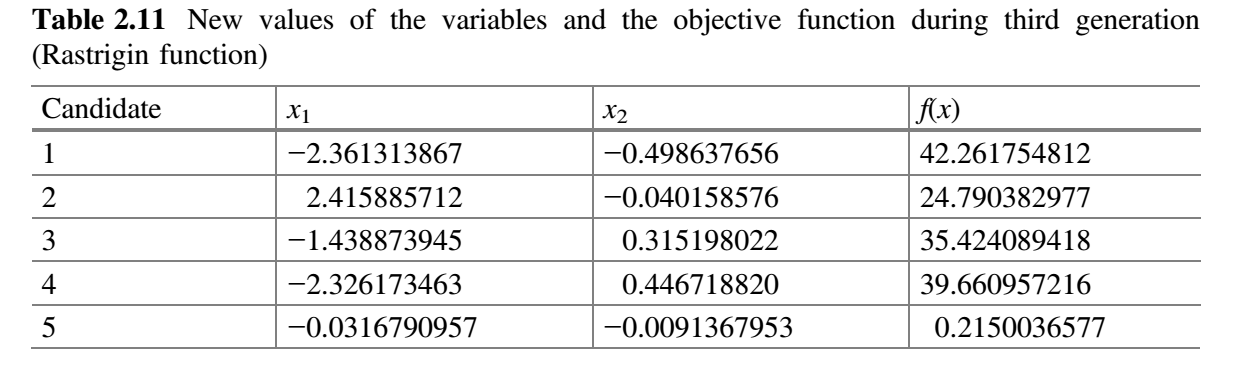
现在，比较表 2.10 和 2.11 的 $f(x)$ 值，并将最佳值放在表 2.12 中。这就完成了 Jaya 算法的第 3 次迭代。

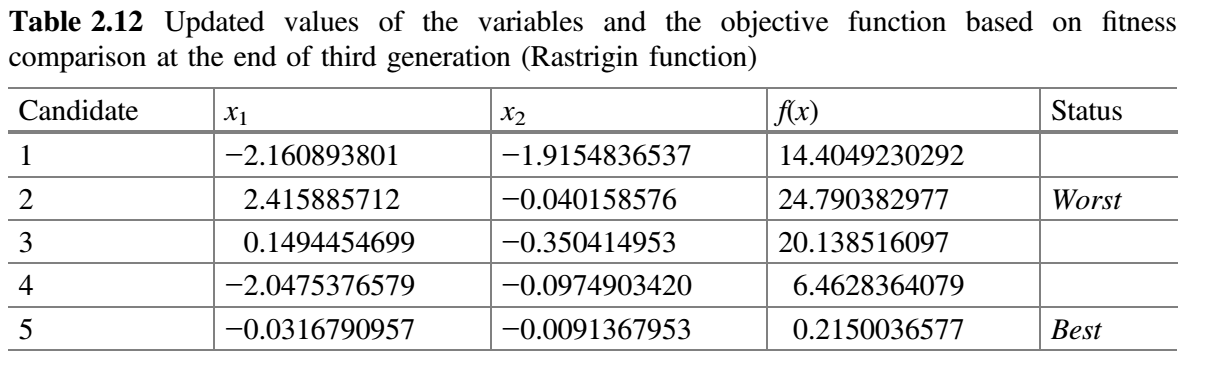
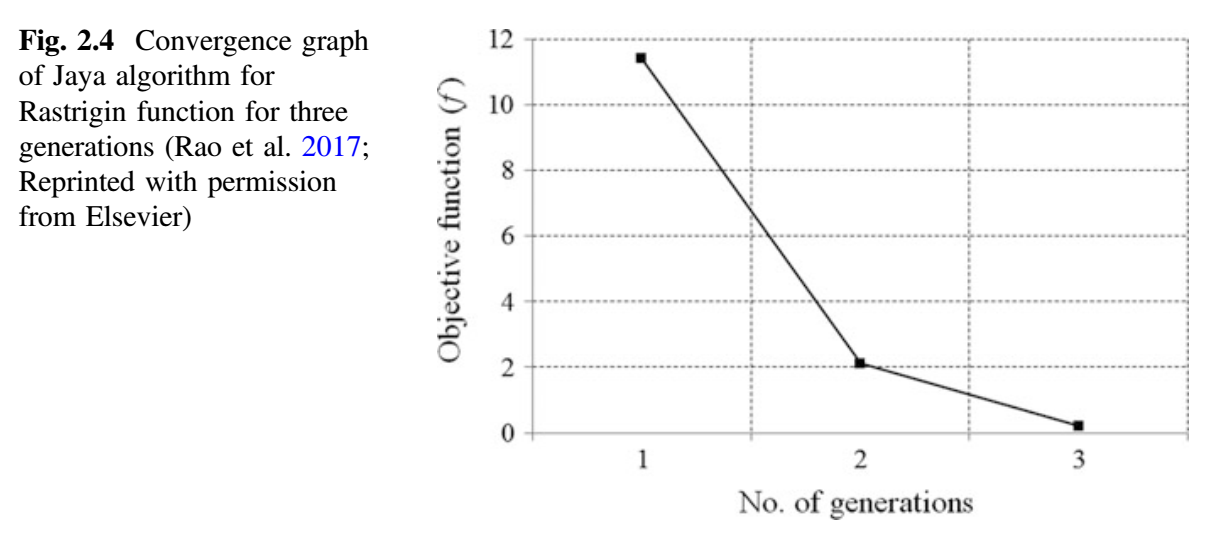
从表 2.12 可以看出，最佳解对应第五个候选解，最差解对应第二个候选解。还可以观察到，目标函数值仅用了三代就从 11.7337857 降至 0.215003677。如果我们增加迭代次数，那么目标函数的已知值（即 0）可以在接下来的几代中达到。在最大化问题的情况下，最佳值是指目标函数的最大值，并相应地进行计算。因此，该方法既可以处理最小化问题，也可以处理最大化问题。下图显示了 Jaya 算法对 Rastrigin 函数的三代收敛图。

约束优化问题的 Jaya 算法演示

为了演示 Jaya 算法，考虑有约束基准函数 Himmelblau。目标函数是找出使 Himmelblau 函数最小化的 $x_1$ 和 $x_2$ 的值。

基准函数：Himmelblau

$$\text{minimize} f(x_i) = (x_1^2 + x_2 - 11)^2 + (x_1 + x_2^2 - 7)^2 \tag {12}$$

约束：

$$g_1(x) = 26 - (x_1 - 5)^2 - x_2^2 \ge 0 \tag {13}$$

$$g_2(x) = 20 - 4x_1 - x_2 \ge 0 \tag {14}$$

变量范围：$-5 \le x_1, x_2 \le 5$。

对于已知解 $x_1 = 3$、$x_2 = 2$，$g_1(x)=18$、$g_2(x) = 6$，这个函数的值为 0。为了演示 Jaya 算法，让我们假设种群规模为 5，两个设计变量为 $x_1$ 和 $x_2$ 以及将 2 次迭代作为终止标准。初始种群在变量范围内随机产生，目标函数的相应值见表 2.13。由于它是一个最小化函数，$f(x)$ 的最小值被认为是最佳值。如果违反了约束条件，则将惩罚分配给目标函数。惩罚的分配方式很多，在这个例子中使用了静态惩罚方法。违反 $g_1(x)$ 的惩罚 $p_1$ 为 $10 * (g_1(x))^2$，违反 $g_2(x)$ 的惩罚 $p_2$ 为 $10 * (g_2(x))^2$。由于这是一个最小化问题，因此惩罚值将被加到目标函数 $f(x)$ 的值上，适应度函数是 $f^{'}(x) = f(x) + 10 * (g_1(x))^2 + 10 * (g_2(x))^2$。函数 $f^{'}(x)$ 称为伪目标函数。

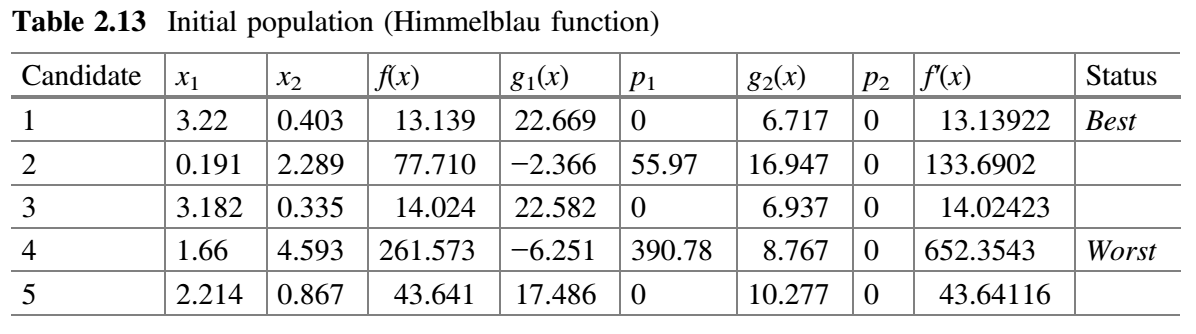
可以注意到，在该示例中，$10 * (g_1(x))^2$ 被用于惩罚违反约束 $g_1(x)$； $10 * (g_2(x))^2$ 被用于惩罚违反约束 $g_2(x)$。更高的惩罚是可取的，可以使用 $50 * (g_1(x))$、$100 * (g_1(x))$ 或 $500 * (g_1(x))$ 或任何其他违反 $g_1(x)$ 的惩罚。对于 $g_2(x)$ 也是如此。惩罚的分配基于优化问题取决于设计者/决策者/用户。

表 2.14 假设 $x_1$ 对应的随机数为 $r_1 = 0.25$、$r_2 = 0.43$，$x_2$ 对应的随机数为 $r_1 = 0.47$、$r_2 = 0.33$。

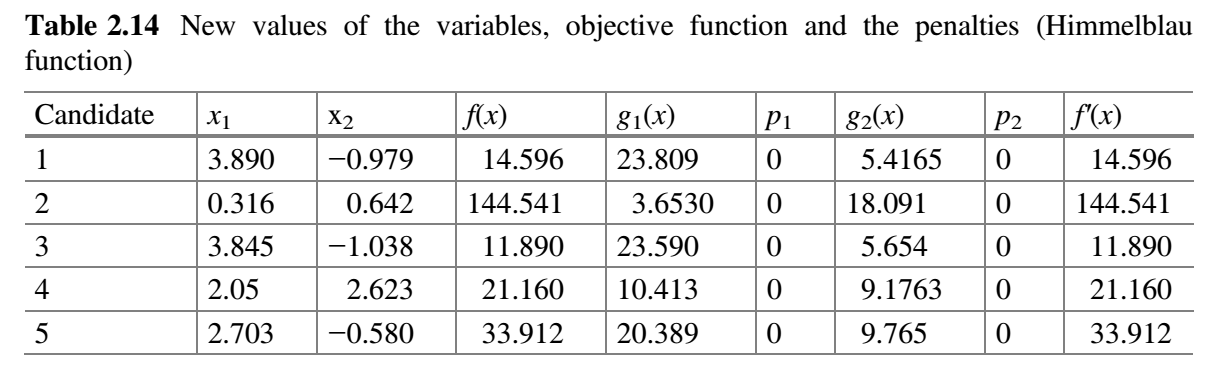
现在，比较表 2.13 和 2.14 的 $f^{'}(x)$ 值，并将最佳值放在表 2.15 中。

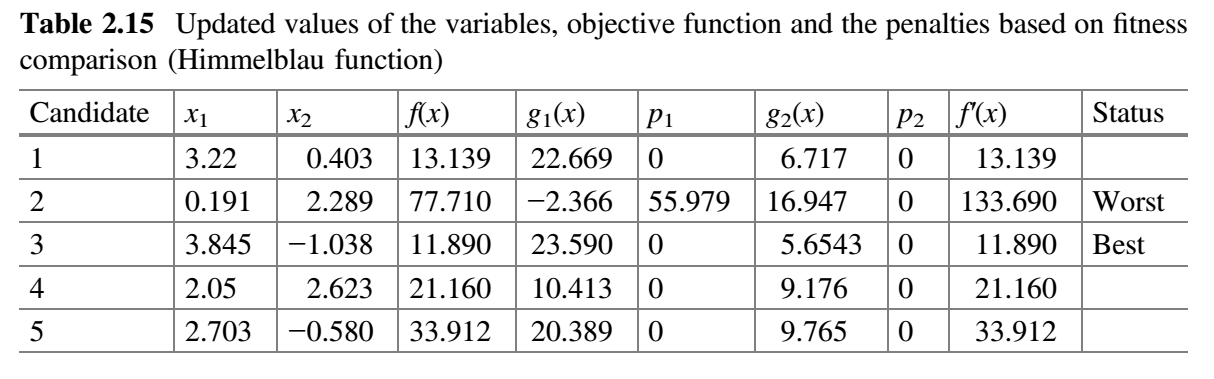
表 2.16 假设 $x_1$ 对应的随机数为 $r_1 = 0.15$、$r_2 = 0.50$，$x_2$ 对应的随机数为 $r_1 = 0.32$、$r_2 = 0.09$。

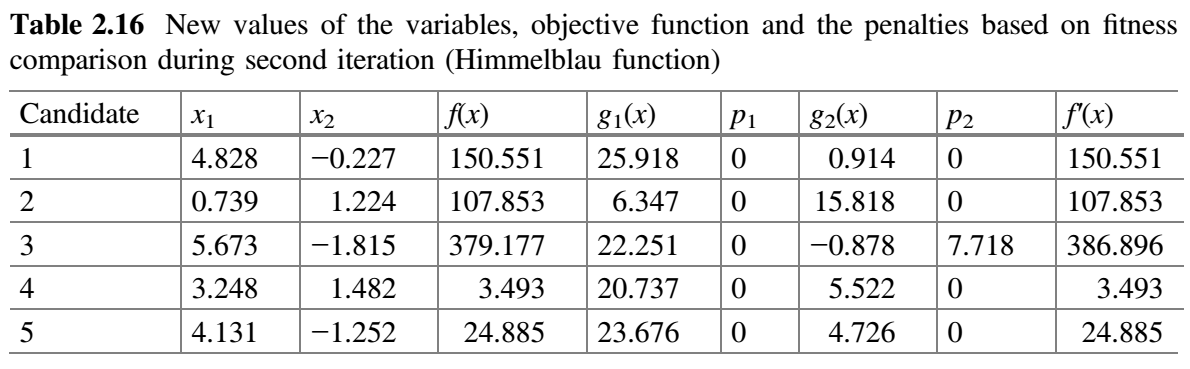
现在，比较表 2.15 和 2.16 的 $f^{'}(x)$ 值，并将最佳值放在表 2.17 中。这就完成了 Jaya 算法的第二次迭代。

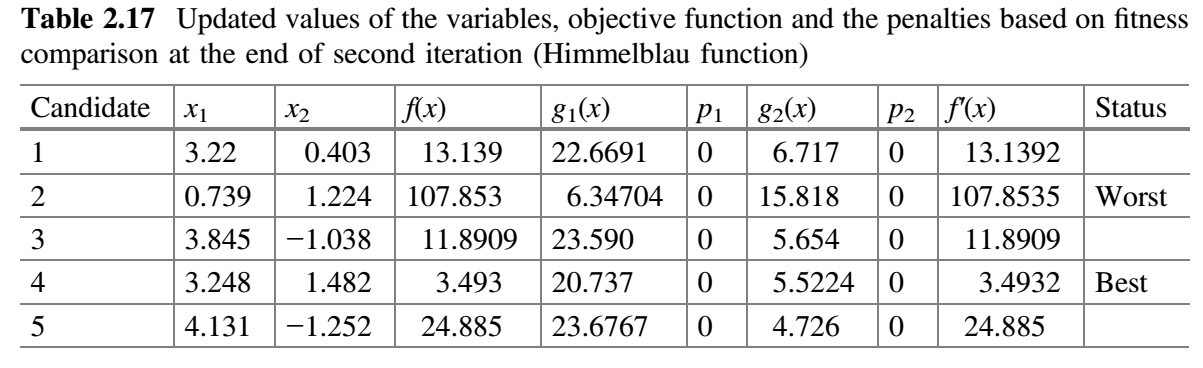
可以注意到，在随机生成的初始种群中，目标函数的最小值为 -13.13922，在第二次迭代结束时，该最小值已经减小到 3.5296。如果我们增加迭代次数，那么目标函数的已知值（即 0）可以在接下来的几次迭代中达到。

需要注意的是，在最大化问题的情况下，最佳值是指目标函数的最大值，并且需要相应地进行计算。在最大化问题中，惩罚需要从目标函数值中减去（也即，$f^{'}(x) = f(x) - 10 * (g_1(x))^2 - 10 * (g_2(x))^2$）。

这里值得提到的是，在公式 (9) 中使用了绝对值 $\vert A(i,j,k) \vert$ 而不是实际值，这提高了算法的探索能力。也可以尝试不使用绝对值，但是在解决不同类型的问题时，可能不会给出更好的结果。

自适应 Jaya 算法

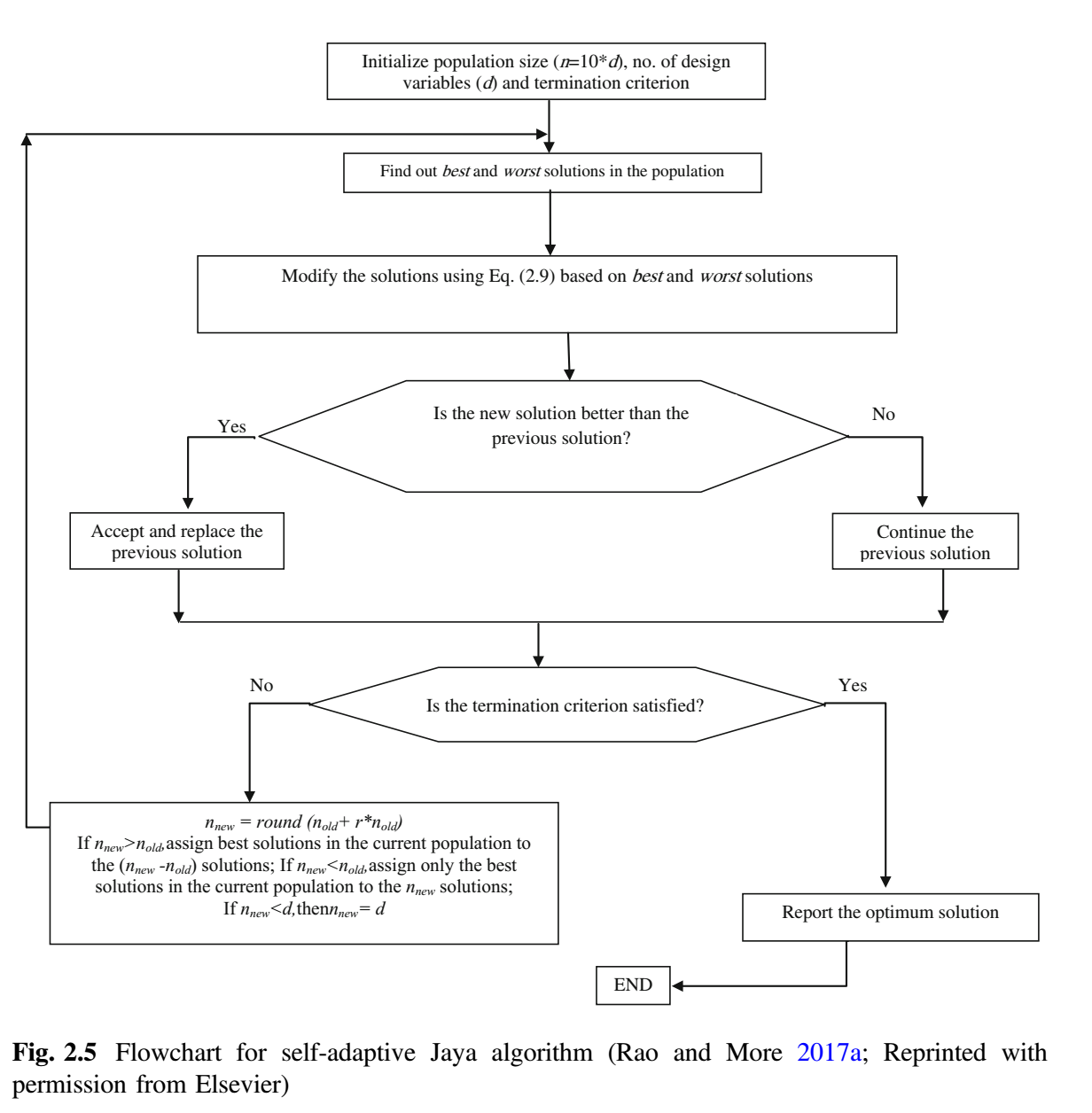
与所有基于种群的算法一样，基本 Jaya 算法需要设置种群规模和迭代次数这样的公共控制参数（但不需要算法相关参数），因此不需要调整这些参数。为特定的情况选择恰当的种群规模是一项艰巨的任务 (Teo 2006)。关于自适应种群规模的研究还不多，因此，提出了这一方面的算法，并称所提出的算法为自适应 Jaya 算法。自适应 Jaya 算法的关键特征是能够自动确定种群规模 (Rao and More 2017a, b)。因此，用户不必考虑选择种群规模。令随机初始种群为 $(10 * d)$，其中 $d$ 是设计变量数，那么新的种群可以表示为，

$$n_{new} = \mathop{ \rm round}(n_{old} + r * n_{old}) \tag {15}$$

其中 $r$ 为取自 $[-0.5, 0.5]$ 之间的随机值，可认为是相对种群发展速度。由于 $r$ 的取值随机，可取正亦可取负，因此种群规模可能减少或增加。例如，如果种群规模 $n_{old}$ 是 20，而生成的随机数 $r$ 是 0.23，则下一次迭代中新种群规模 $n_{new}$ 将是 25 （根据公式 (15)）。如果产生的随机数 $r$ 是 - 0.16，则下一次迭代中新种群规模 $n_{new}$ 将为 17。

提出的自适应 Jaya 算法的流程图如下所示。精英策略将在下一代种群规模大于当前种群规模时实施的（$n_{new} \gt n_{old}$）。那么所有现存种群都将进入下一代，当前种群中的最佳解被分配到剩余的 $n_{new} - n_{old}$ 个解中。当下一代种群规模小于当前种群规模（$n_{new} \lt n_{old}$）时，只有当前最好的解才能进入下一代。如果下一代和当前种群规模相等（$n_{new} = n_{old}$），则不会发生变化。如果种群规模减小且小于设计变量数 $d$，则令种群规模等于设计变量数（如果 $n_{new} \lt d$，则 $n_{new} = d$）。因此，解就不会陷入局部最优。

基于拟反向的 Jaya（QO-Jaya）算法

为了进一步提高种群多样化，提高 Jaya 算法的收敛速度，在 Jaya 算法中引入了反向学习（opposition based learning）的概念。为了获得更好的近似，生成与当前种群相反的种群，并同时考虑两者。但是，为了保持 Jaya 算法的随机性，需要生成拟反向的（quasi-opposite）种群。候选解的变量的拟反向值不是变量的镜像点，而是一个在搜索空间中心和变量镜像点之间随机选择的值。拟反向种群使用方程 (16)-(18) 产生。

$$A_{i,j,k}^q = \mathop{\rm rand} (a, b) \tag {16}$$

$$a = \frac{A_k^L + A_k^U}{2} \tag {17}$$

$$b = A_k^L + A_k^U - A_{i,j,k} \tag {18}$$

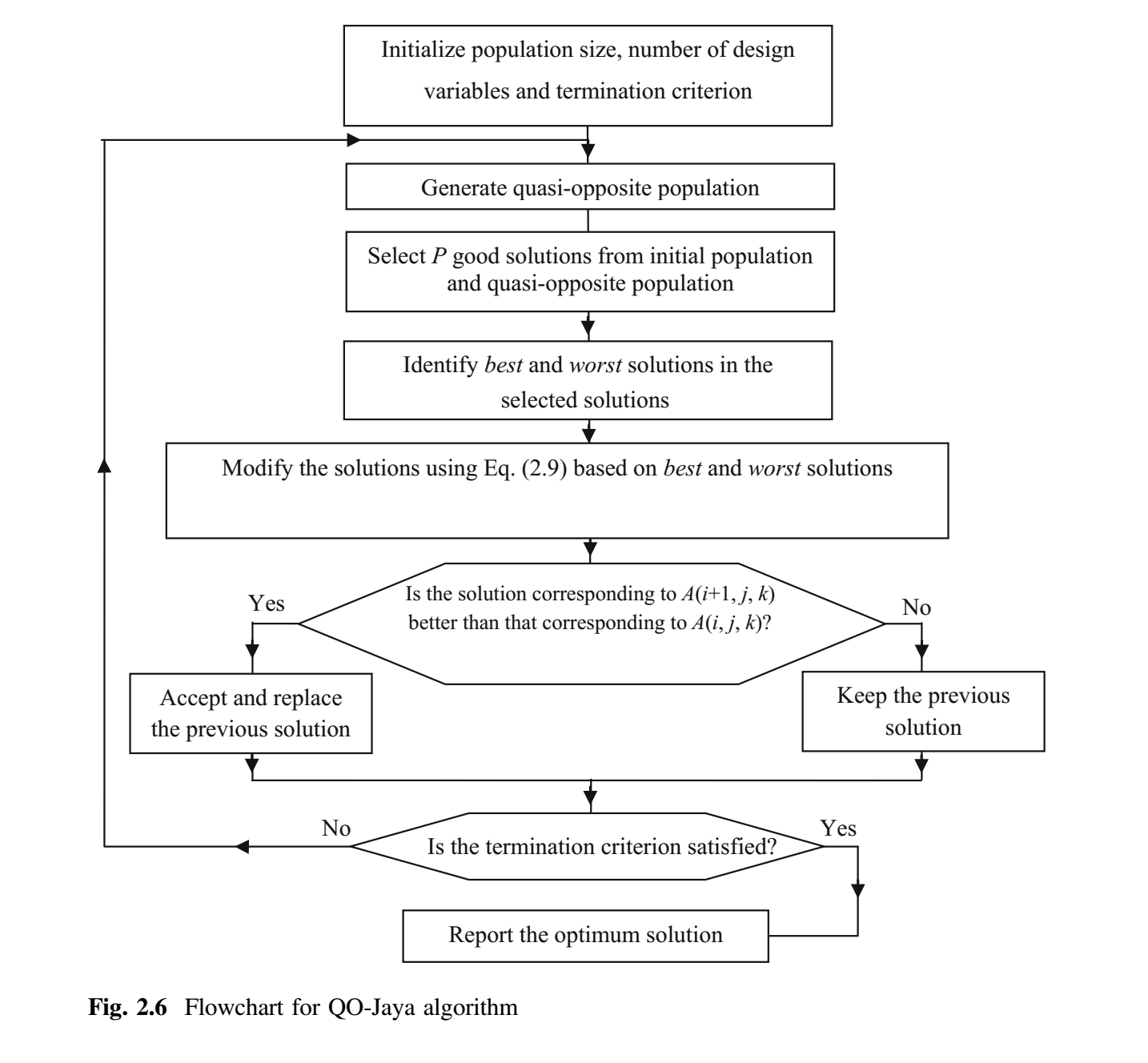
$i = 1, 2, 3, \dots, g$，$j = 1,2,3,\dots,P$，$k = 1,2, 3, \dots, d$。其中，$A_k^L$ 和 $A_k^U$ 是第 $k$ 个变量的下限值和上限值，$A_{i,j,k}^q$ 是 $A_{i,j,k}$ 的拟反向值。例如，如果变量的下限和上限分别为 10 和 60，且当前迭代中变量 $A_{i,j,k}$ 的值为 23，则 $a = 35$（给定范围的中值）， $b = 10 + 60 - 23 = 47$。事实上，完全反向值（镜像点）是 47。而变量的拟反向值 $A_{i,j,k}^q = rand(35, 47)$。这意味着，将会生成 35 到 47 之间的任何值。下图给出了 QO-Jaya 算法的流程图 (Rao and Rai 2017a, b)。 QO-Jaya 算法所需的函数评估次数 = 种群规模 $\times$ 迭代次数。

自适应多种群（SAMP）Jaya 算法

基于多种群的（multi-population based）高级优化方法, 用于提高搜索的多样性。该方法通过将整个种群分成多个组（子群）并在整个搜索空间分配这些子群，从而可以有效检测问题的变化。其基本思想是通过将不同的子群分配到不同的区域来保持搜索过程的多样性。每个子群都受到算法搜索过程多样性或集中性的影响。当观察到解发生变化时，子群之间的相互作用通过合并和分割（merge and divide）过程进行。多种群方法在处理各种不同问题时是高效的，该方法优于现有的针对不同问题的固定种群规模方法。多种群方法对保持种群多样性有帮助。搜索过程的总体多样性可以通过将整个种群分配到不同子群来保持, 因为不同的子群可以位于问题搜索空间的不同区域，因此具有在不同区域同时搜索的能力。

子群数量的选取是算法性能的一个关键问题，与问题的复杂性有关。在搜索过程中，子群规模不断变化。在子群中的解可能也不足以满足足够的多样性。为了解决这些问题，提出了一种自适应多种群（self-adaptive multi-population，SAMP） Jaya 算法来求解工程优化问题。为了有效地监测问题景观（landscape）的变化，SAMP 算法基于问题景观的改变强度自适应地改变子群的数量。对基本 Jaya 算法进行了如下修改：

  • 提出的 SAMP-Jaya 算法基于解的质量将整个群体划分为多个子群。将子群分布到整个搜索空间而不是集中于某个区域。因此提出的算法被期望产生最优解。
  • 搜索过程中，SAMP-Jaya 算法基于问题景观的变化强度来修改子群的数量。这意味着子群的数量会增加或减少。在 SAMP-Jaya 算法中, 子群的数量基于解的强度变化自适应地进行修该。此特性支持搜索过程中追踪最优解，提高了搜索过程的多样性。此外，重复解被新产生的解替代以维持多样性和增强探索过程。

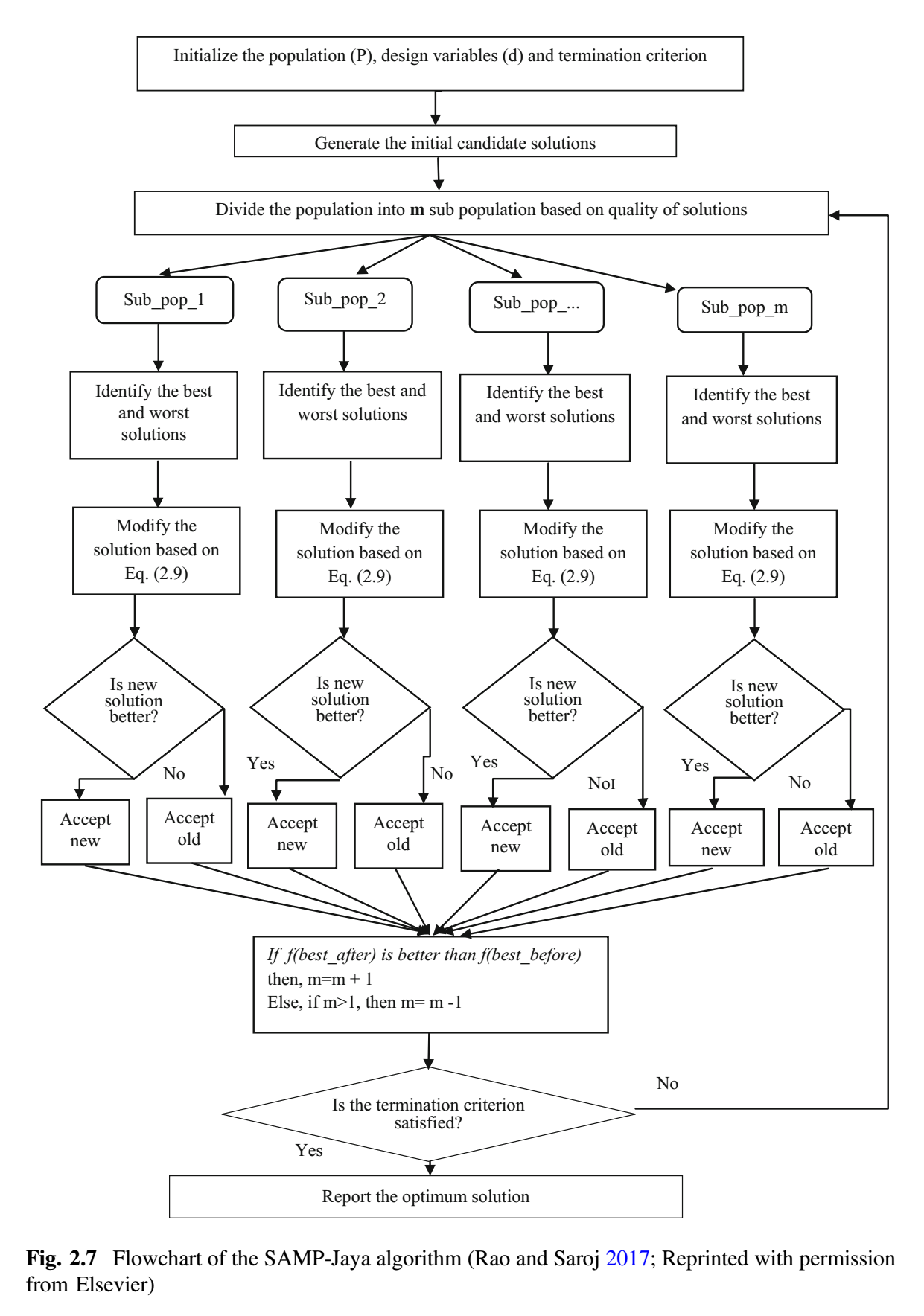
上图给出了 SAMP-Jaya 算法的流程图 (Rao
and Saroj 2017)。SAMP-Jaya 算法的基本步骤如下：

  1. 从设置设计变量 $d$、种群数量 $P$ 和停止准则开始。
  2. 下一步是基于定义的适应度函数（对于特定的问题），计算初始解。
  3. 根据解的质量, 将整个种群划分为 $m$ 个子群（最初考虑 $m=2$）。
  4. 每个子群都独立地使用 Jaya 算法修改（更新）子群中的解。接受修改的解，当且仅当他比旧解好。
  5. 合并所有子群。检查 $f(best \_ before)$ 是否优于 $f(best \_ after)$。这里，$f(best \_ before)$ 是之前整个子群最佳解，$f(best \_ after)$ 是当前整个种群的最佳解。如果 $f(best \_ after)$ 的值优于 $f(best \_ before)$ 的值，则 $m$ 加 1（即 $m = m + 1$），目的是增加搜索过程的探索特征。否则，$m$ 减 1（即 $m = m - 1$），因为算法需要更多的开发能力。
  6. 检查停止条件。如果已达到终止条件，则结束循环并给出最佳解。否则，(a) 用随机生成的解替换重复的解；(b) 按步骤 3 重新划分子群并重新执行后续步骤。

无约束优化问题的 SAMP-Jaya 算法演示

为了演示 Jaya 算法，考虑无约束基准函数 Sphere。目标函数是找出使 Sphere 函数值最小的 $x_i$ 的值。

$$\text{minimize} f(x_i) = \sum_{i=1}^m x_i^2 \tag {19}$$

变量范围：$- 100 \le x_i \le 100$。

这个基准函数的已知解是所有的 $x_i$ 值为 0，其函数值为 0。为了演示 SAMP-Jaya 算法，假设种群规模为 20，子群的初始数量为 2，有两个设计变量 $x_1$ 和 $x_2$ 以及将两次迭代作为终止准则。初始种群在变量范围内随机产生，目标函数的相应值见下表。

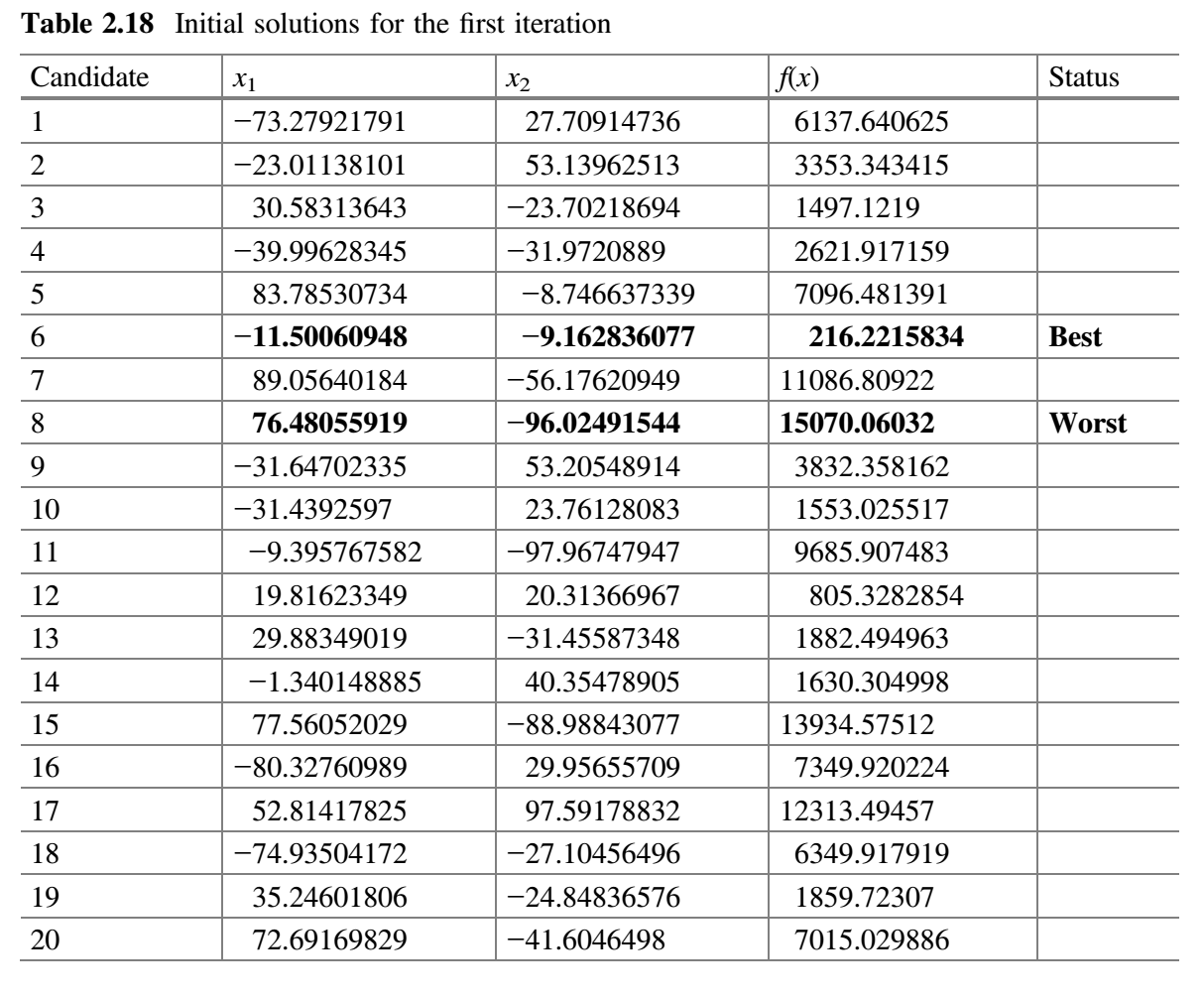
SAMP-Jaya 算法的各个步骤给出如下：

  1. 设计变量数 $d = 2$、种群规模 $P = 20$、子群（初始）= 2、终止准则 = 2 次迭代。
  2. 下一步是计算问题的初始解。
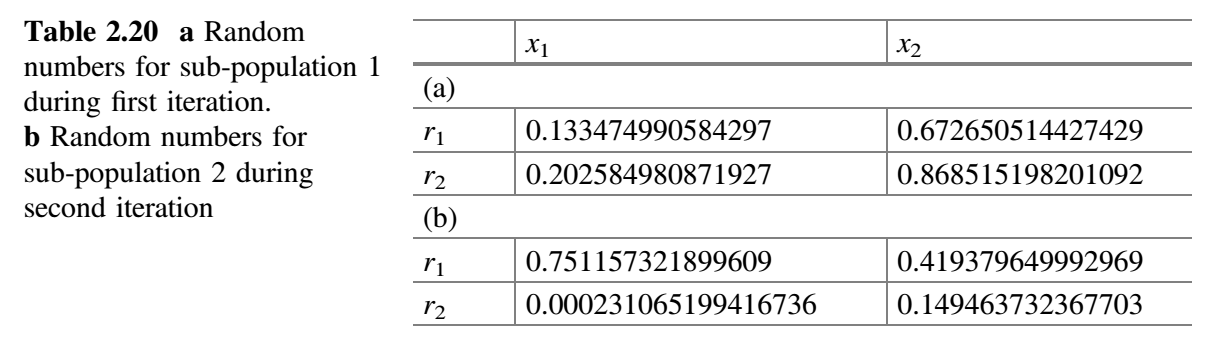
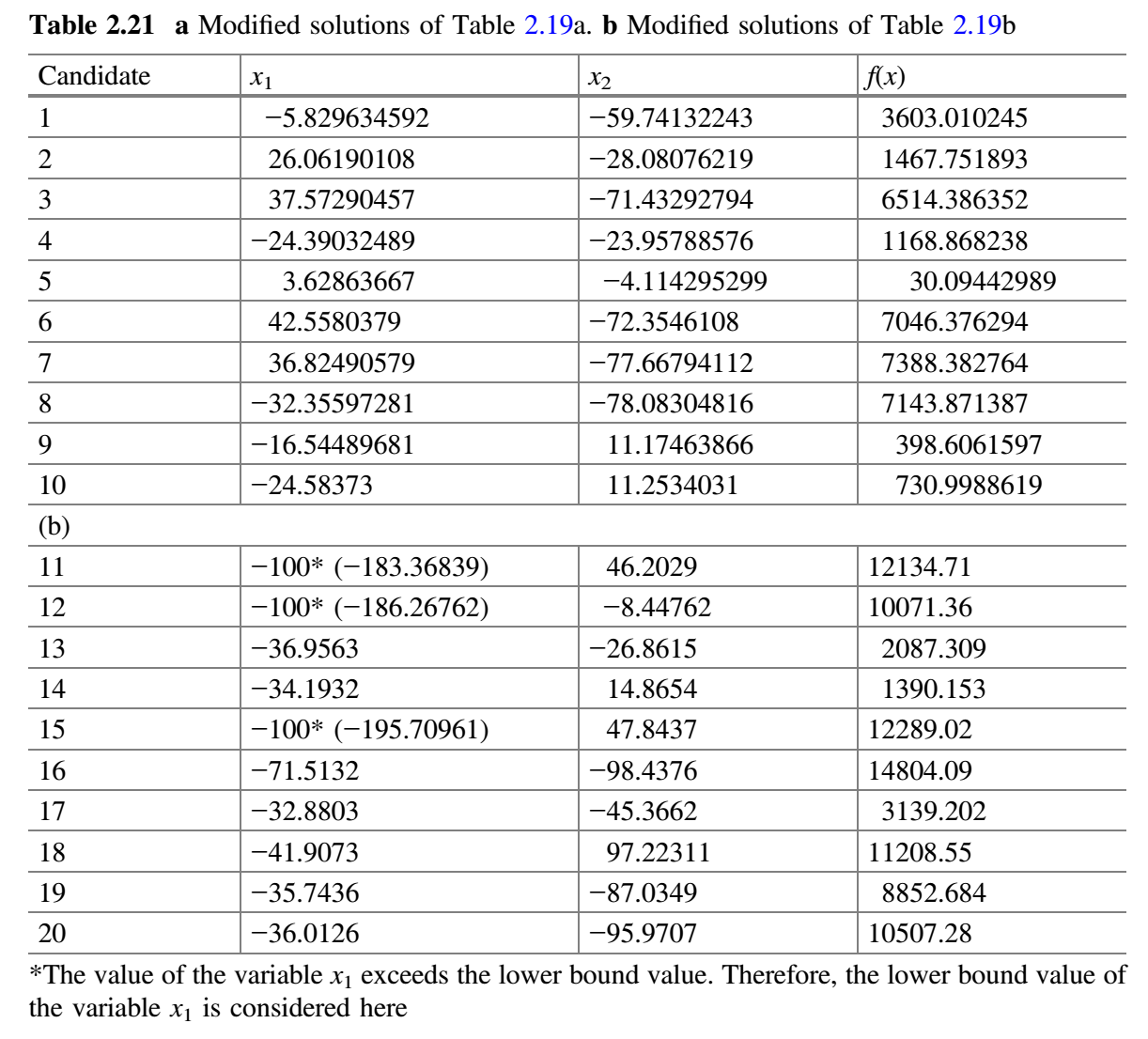
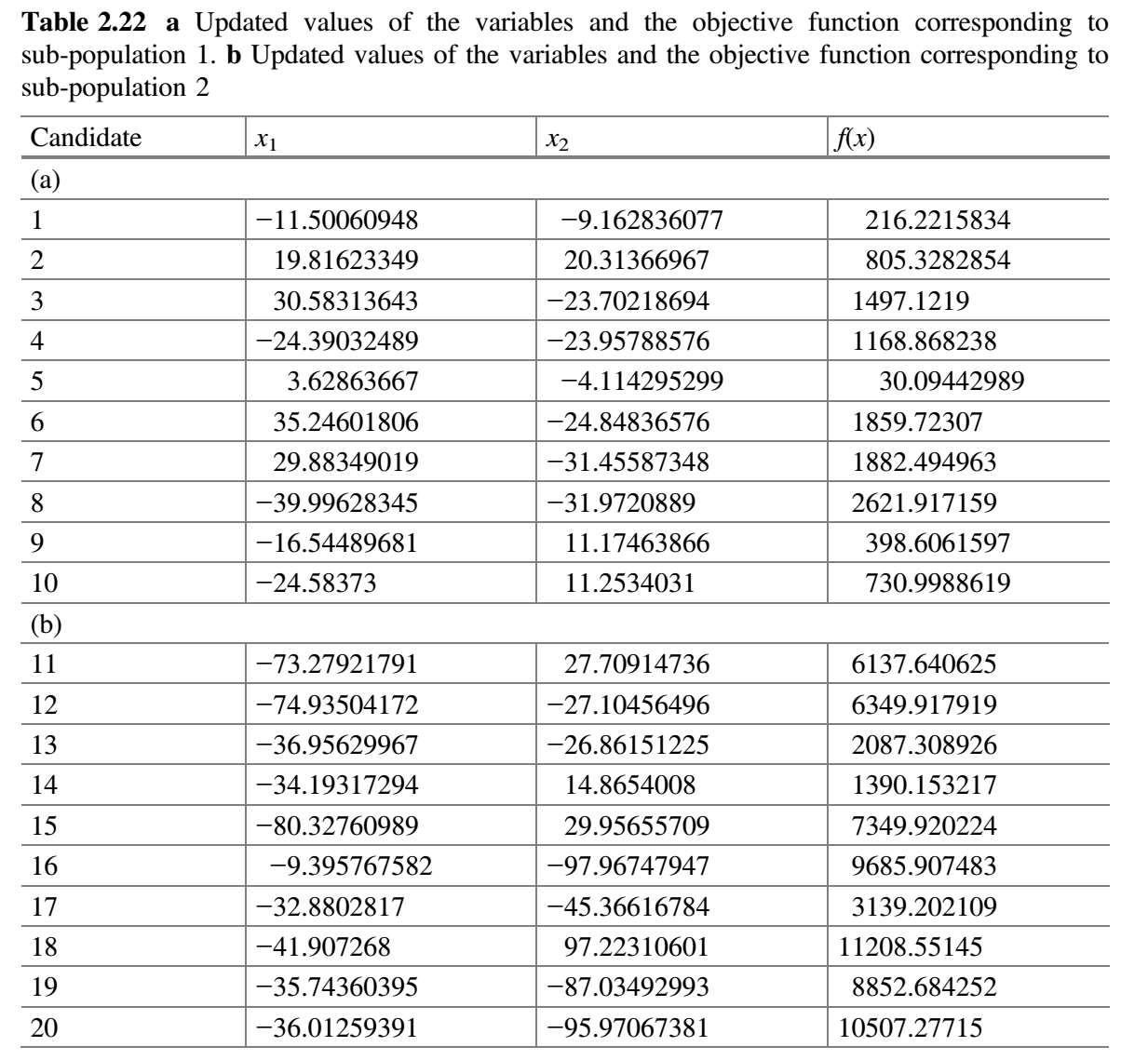
  3. 根据解的质量，将整个种群分为 $m$ 组（初始考虑 $m = 2$）。
  4. 每个子群独立地使用 Jaya 算法更新子群中的解。每个修改解只有在优于旧解时才被接受。表 2.20a、2.20b 分别展示了用于子群 1 和 2 的随机数。现在，比较表 2.19a 和 2.21a，更新值（即更好的值）保留在表 2.22a 中。类似地，比较表 2.19b 和 2.21b，更新值（即更好的值）保留在表 2.22b 中。
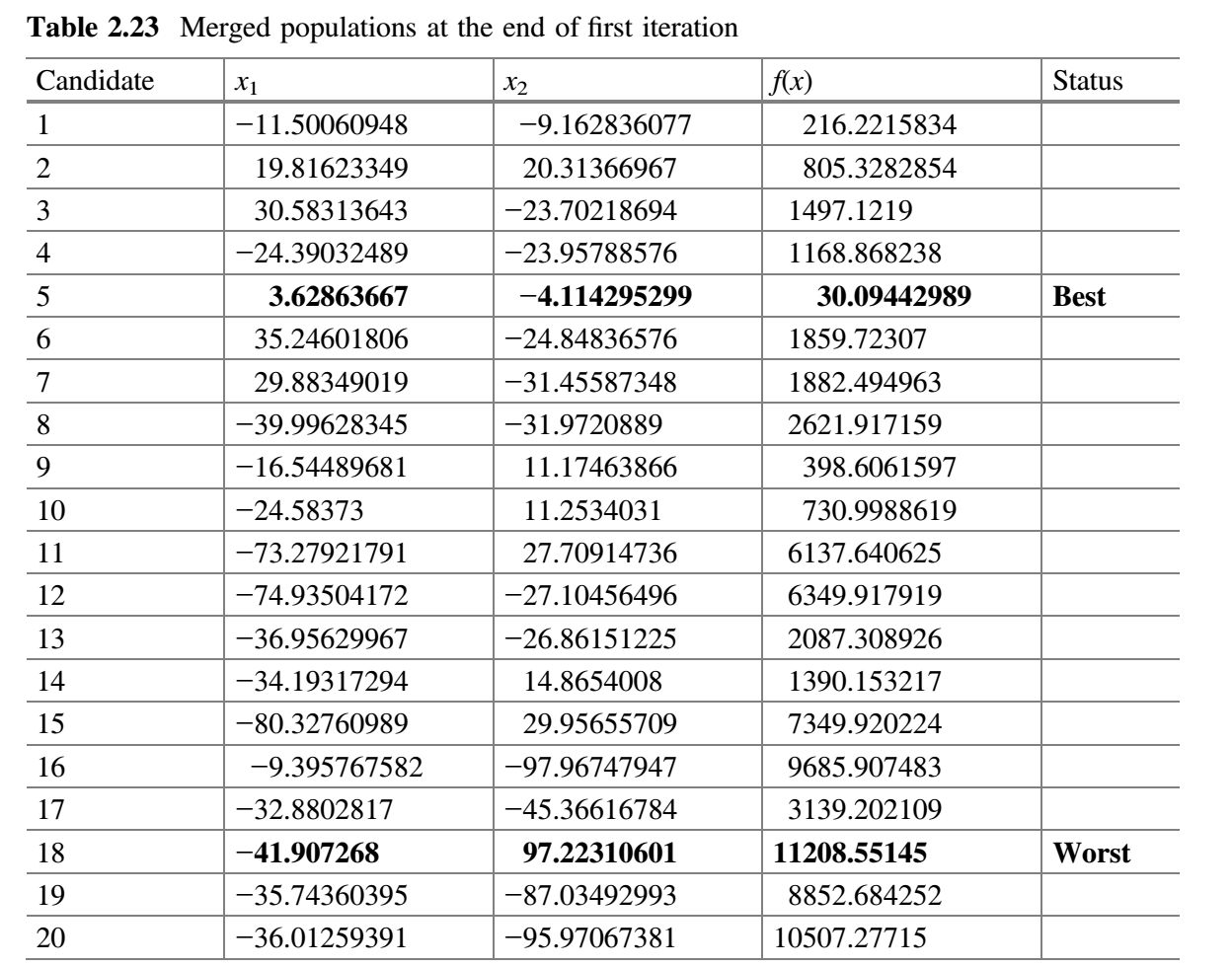
  5. 合并所有子群。表 2.23 显示了第一次迭代结束时合并的种群。
    检查 $f(best \_ before)$ 是否比 $f(best \_ after)$ 好。这里，$f(best \_ before)$ 是先前整个种群的最佳解，$f(best \_ after)$ 是当前整个种群的最佳解。在第一次迭代结束时，发现的 $f(best \_ after)$ 值比 $f(best \_ before)$ 的值好，因此 $m$ 加 1（即 $m = 2 + 1 = 3$），其目的是增加搜索过程的探索特征。
  6. 检查终止条件。如果达到终止条件，则终止循环并报告最佳解。由于在本示例中终止条件被定为 2 次迭代，因此该过程跳到步骤 3 而并重复（表 2.24）。

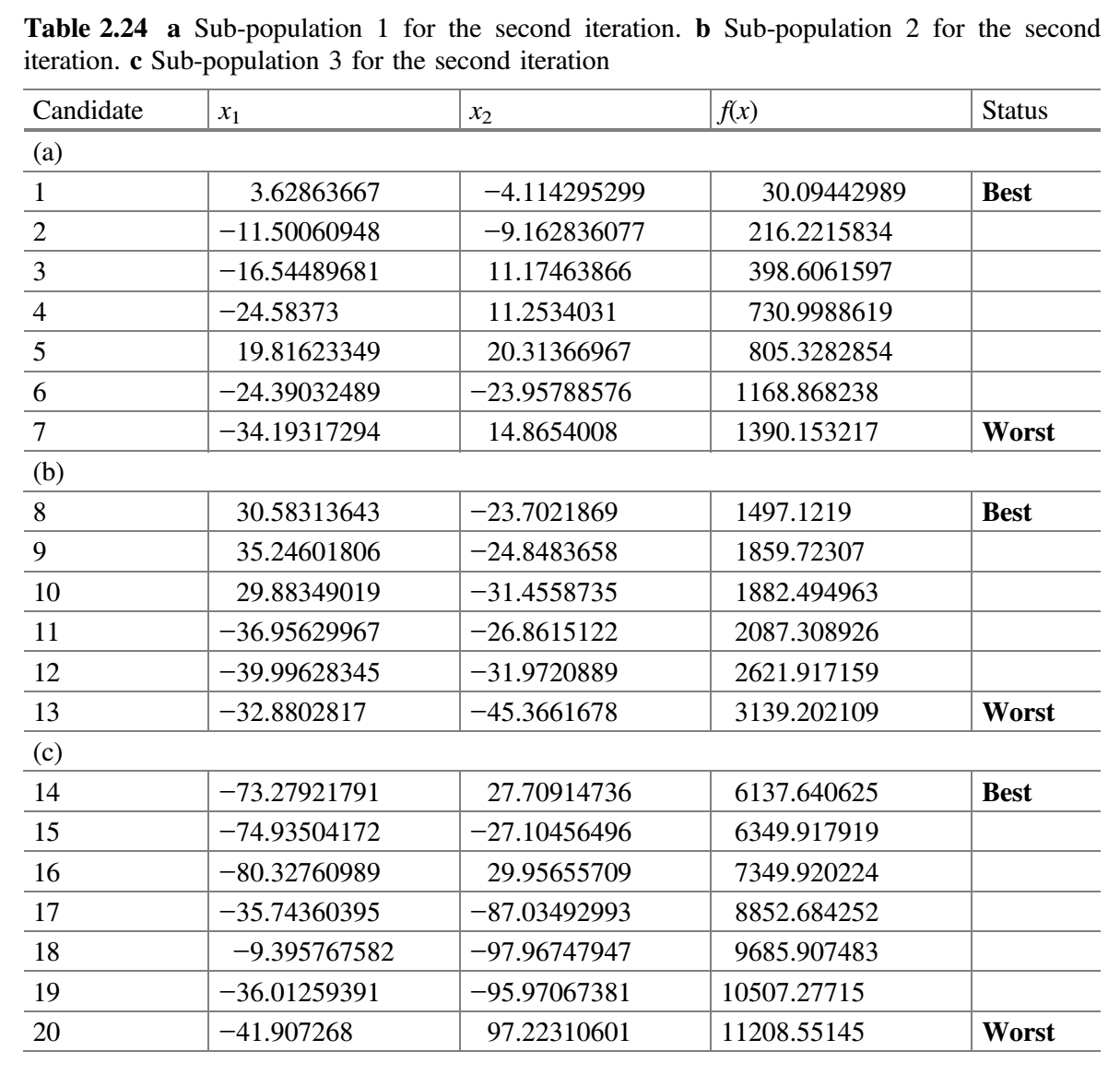
第 2 次迭代：

  1. 根据解的质量，将整个种群分成 3 组。
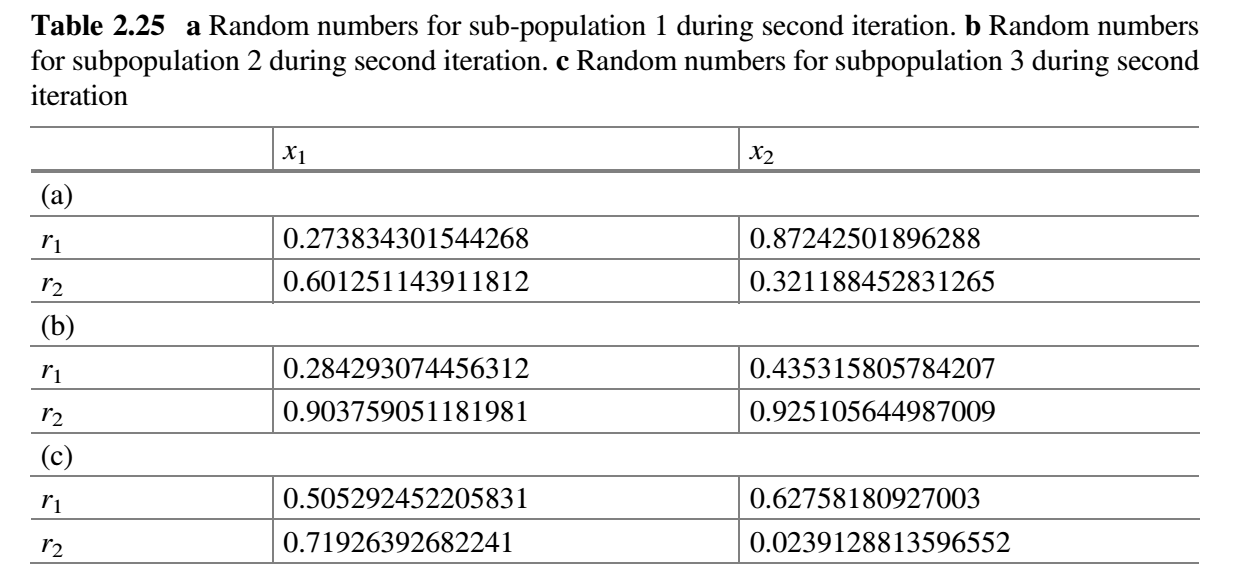
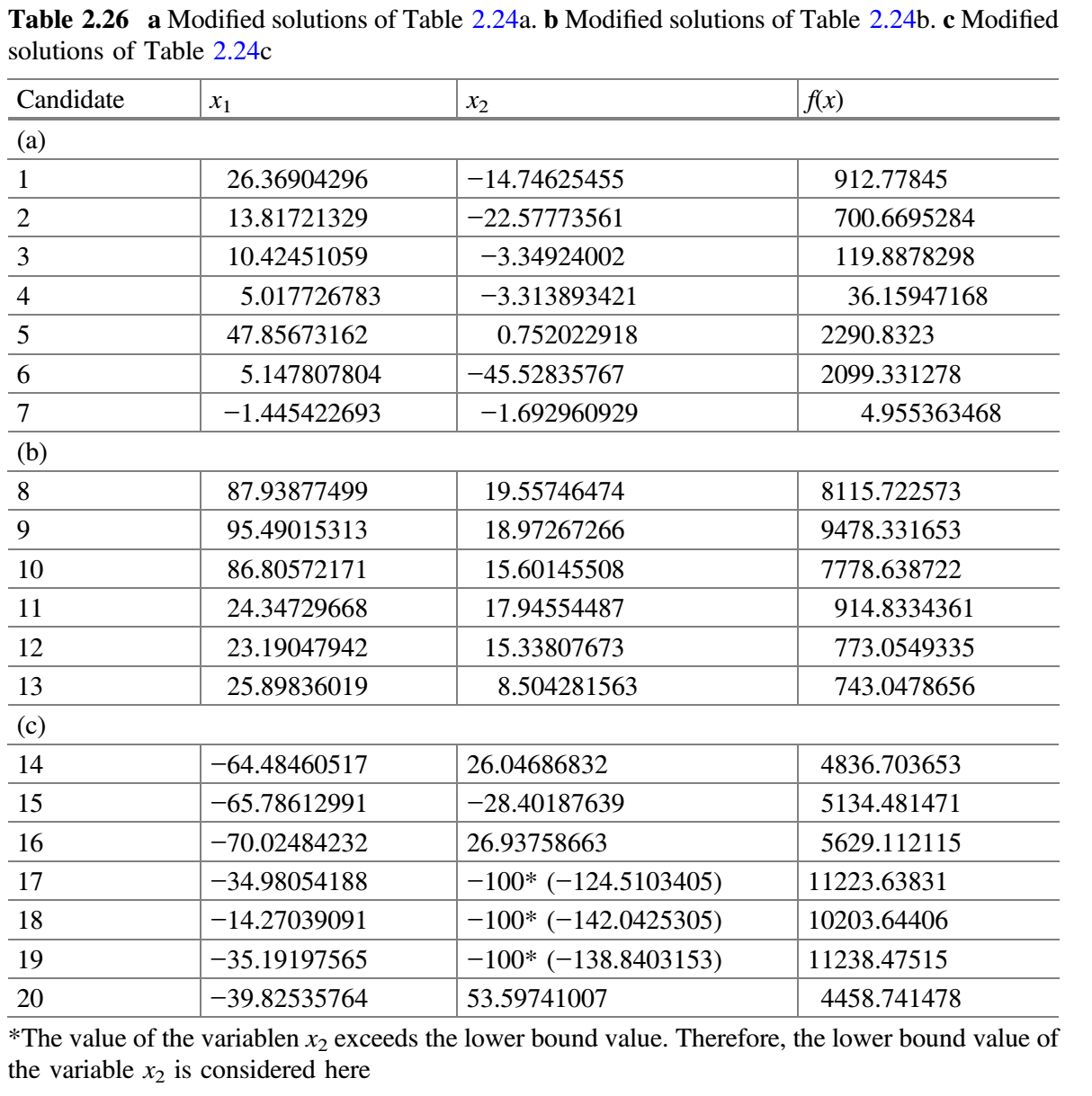
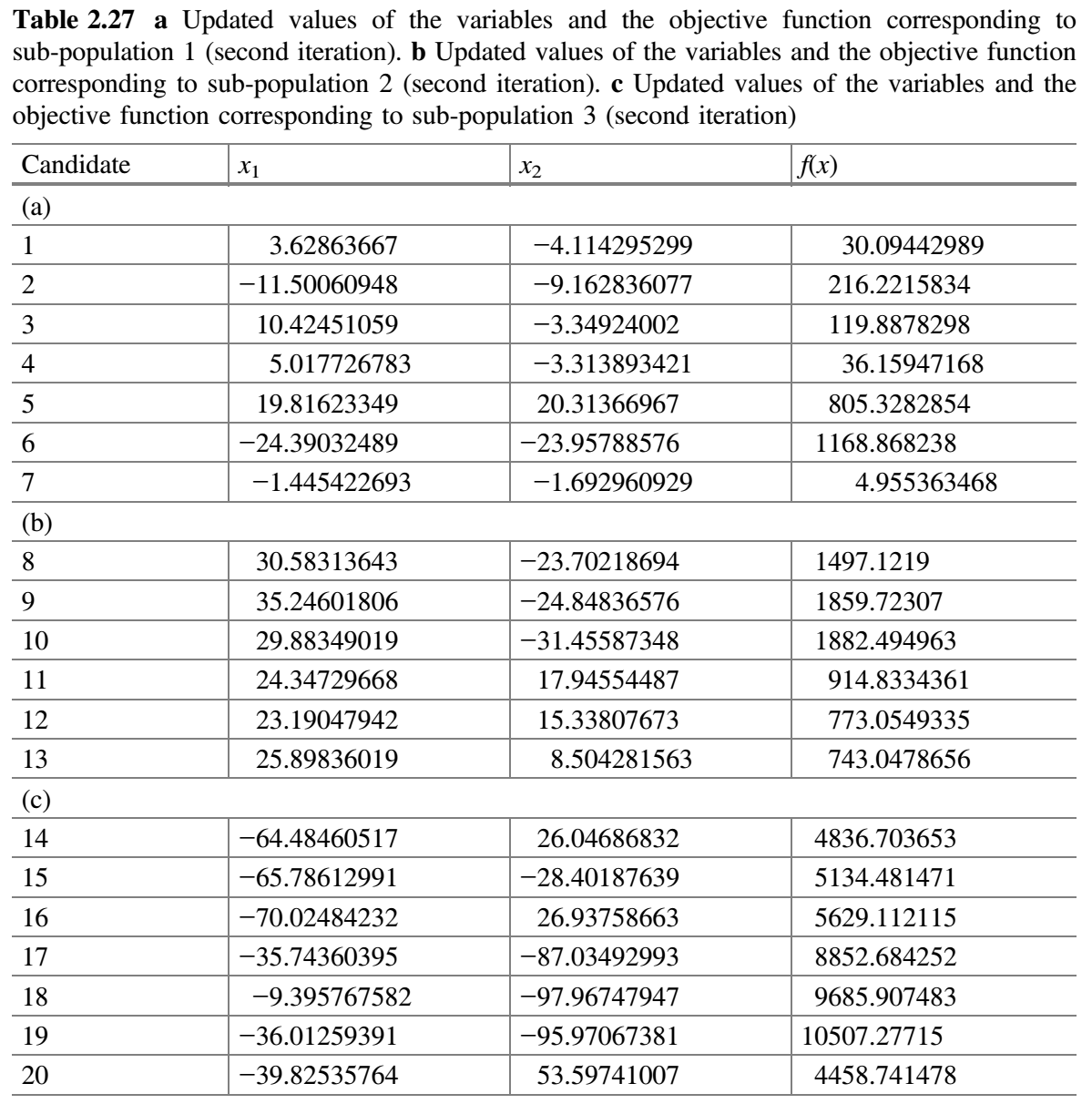
  2. 每个子群独立使用 Jaya 算法更新解。修改的解只有在优于旧解时才被接受。表 2.25a-c 分别显示了用于子群 1、2 和 3 的随机数。比较表 2.24a 和 2.26a，更新值保存在表 2.27a 中。同样，比较表 2.24b 和 2.26b，更新值保存在表 2.27b 中。同样，比较表 2.24c 和 2.26c，更新值保存在表 2.27c 中。
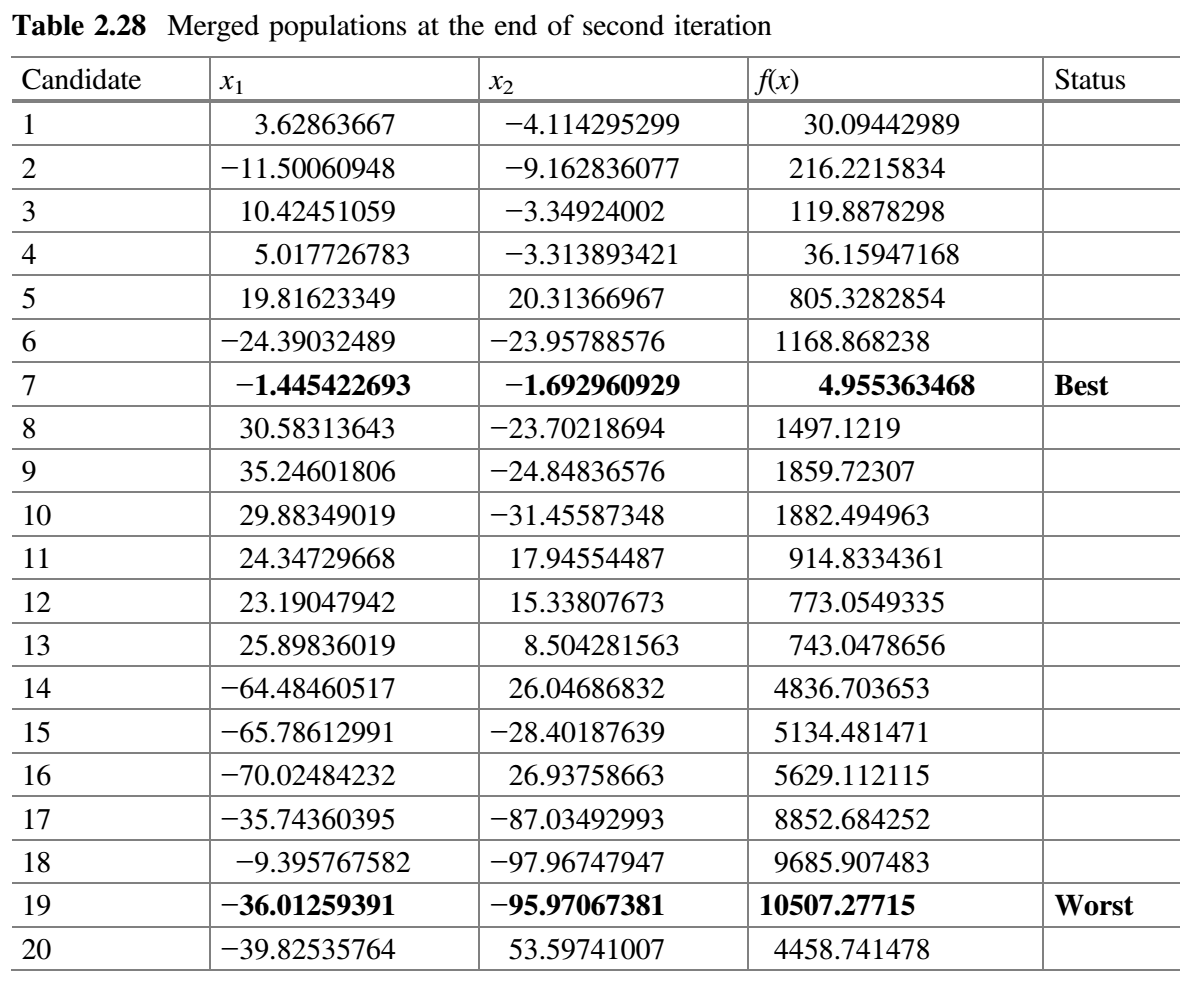
  3. 合并所有子群。表 2.28 显示了第二次迭代结束时合并的种群。检查 $f(best \_ after)$ 是否比 $f(best \_ before)$ 好。在第二次迭代结束时，发现 $f(best \_ after)$ 的值比 $f(best \_ before)$ 的值好，因此 $m$ 加 1（即 $m = 3 + 1 = 4$）。
  4. 检查停止条件。如果达到停止条件，则终止循环并报告最佳解。否则，该过程将继续，直到达到终止标准。在本示例中，终止条件被定为 2 次迭代，因此该过程被终止。

自适应多种群精英策略（SAMPE）Jaya 算法

SAMPE-Jaya 算法对基本 Jaya 算法进行了以下修改：

  • 提出的算法基于解的质量将种群划分为多个子群。此外，劣势群体（适应度值低的群体）的最差解被优势群体（适应度值高的群体）的解（精英解）所取代。使用多个子群将解分布于搜索空间，而不是集中在特定区域。因此，该算法可望产生最优解，并监测问题景观的变化。
  • 在搜索过程中，SAMPE-Jaya 算法根据监测到的问题景观的变化强度修改子群的数量。此外，为了保持多样性和加强探索过程，用新生成的解替换重复的解。

SAMPE-Jaya 算法的基本步骤如下：

  1. 从设计变量数量 $d$、种群规模 $P$、精英规模 $ES$ 和终止标准的设置开始。
  2. 下一步是根据问题定义函数计算初始解。
  3. 根据解的质量，将整个种群分为 $m$ 组，用精英解代替劣势解（与 $ES$ 相等）。
  4. 每个子群体独立使用 Jaya 算法修改解。修改的解只有在优于旧解时才会保留。
  5. 合并使用子群。检查 $f(best \_ before)$ 是否优于 $f(best \_ after)$。这里，$f(best \_ before)$ 是之前整个子群最佳解，$f(best \_ after)$ 是当前整个种群的最佳解。如果 $f(best \_ after)$ 的值优于 $f(best \_ before)$ 的值，则 $m$ 加 1（即 $m = m + 1$），目的是增加搜索过程的探索特征。否则，$m$ 减 1（即 $m = m - 1$），因为算法需要更多的开发能力。
  6. 检查终止条件。如果搜索过程达到停止标准，则终止循环并报告最佳解。否则，(a) 用随机生成的解替换重复解；(b) 按照步骤 3 重新划分子群，然后执行后续步骤。

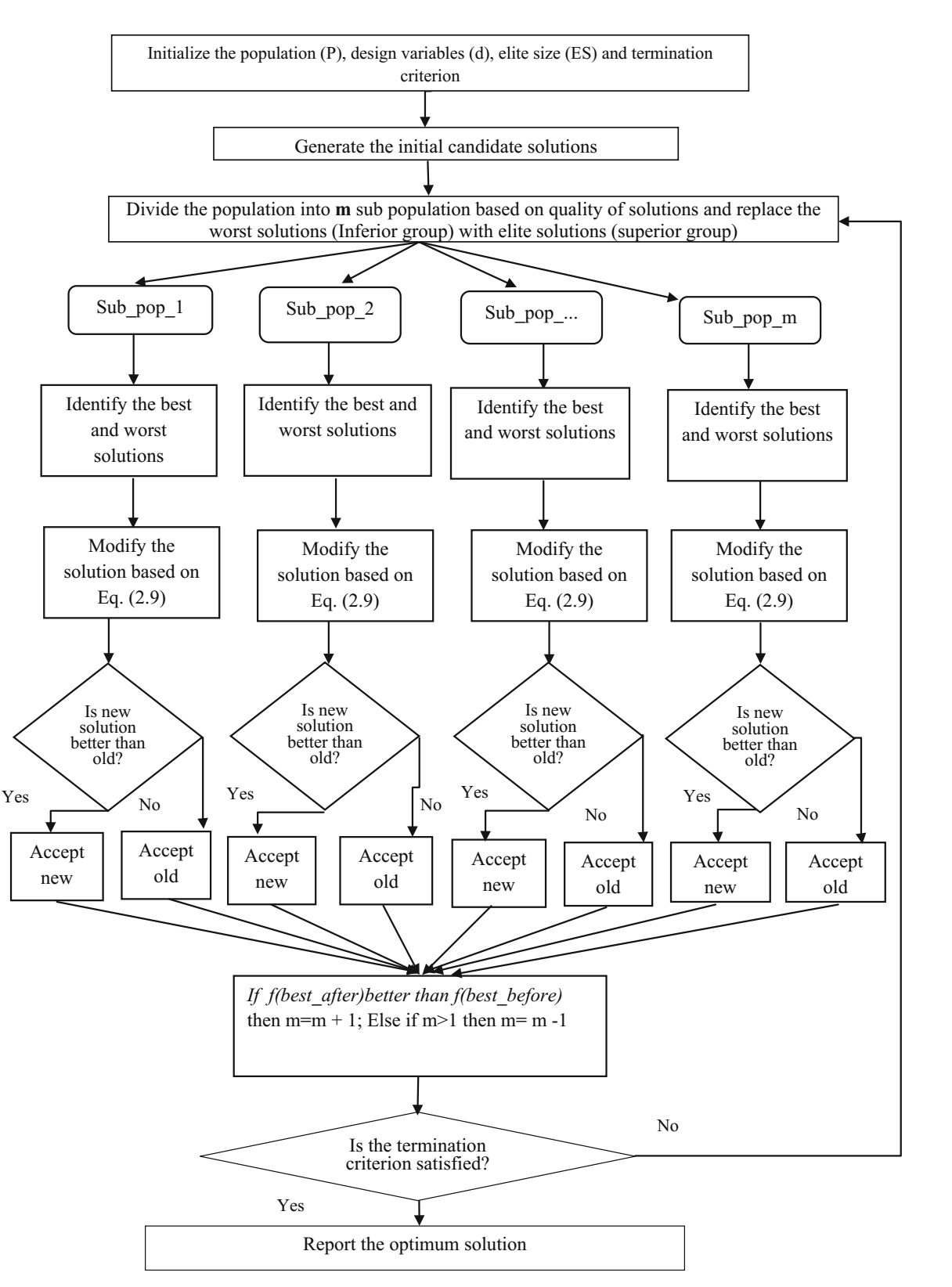
上图显示了 SAMPE-Jaya 算法的流程图。

混沌 Jaya 算法

一种基于混沌理论的 Jaya 算法变体被称为混沌-Jaya（Chaotic-Jaya，CJaya）算法。其目的是为了提高收敛速度，更好地探索搜索空间而不陷入局部最优。CJaya 算法的工作原理与 Jaya 算法完全相似，唯一不同的是 CJaya 算法中的随机数是利用混沌随机数发生器产生的。例如，如果将帐篷映射混沌函数用作混沌随机数发生器（chaotic random number generator），例如，如果使用帐篷映射（tent map）混沌函数作为混沌随机数发生器，则它可由等式 (20) 表示。

$$
x_{k+1} =
\begin{cases}
\frac {x_k}{0.7} & x_k \lt 0.7 \
\frac {10}{3}(1-x_k) & x_k \ge 0.7
\end{cases}
\tag {20}
$$

其中，$x_{k+1}$ 是新产生的混沌随机数，$x_k$ 是先前产生的混沌随机数。

多目标 Jaya（MO-Jaya）算法

MO-Jaya 算法是为解决多目标优化问题而开发的 (Rao et al. 2017)。MO-Jaya 算法是求解多目标优化问题的 Jaya 算法的后验版本。MO-Jaya 算法中解以类似于 Jaya 算法中等式 (9) 的方式更新。然而，为了有效地处理多个目标，MO-Jaya 算法结合了非支配排序方法和拥挤距离计算机制。非支配排序和拥挤距离机制的概念已在第 2 节中解释过。

在单目标优化的情况下，根据目标函数值很容易确定一个解比另一个解好。但是在存在多个冲突的目标的情况下，从一组解中确定最好和最差的解是困难的。在 MO-Jaya 算法中，通过基于约束-支配概念、非支配概念和拥挤距离值比较分配给解的秩来完成确定最佳解和最差解的任务。

首先，随机生成具有 $NP$ 个解初始种群。然后根据约束-支配和非支配概念对初始种群进行排序。首先根据约束-支配概念确定解之间的优越性，然后根据非支配概念确定解之间的拥挤距离值。秩较高的解被认为优于解。如果两个解具有相同的秩，那么拥挤距离值较高的解被认为优于另一个解。这可确保从搜索空间的稀疏区域中选择解。选择秩最高的解（秩 = 1）作为最佳解。秩最低的解被选为最差解。一旦选择了最佳解和最差解，将根据等式 (9) 更新解。

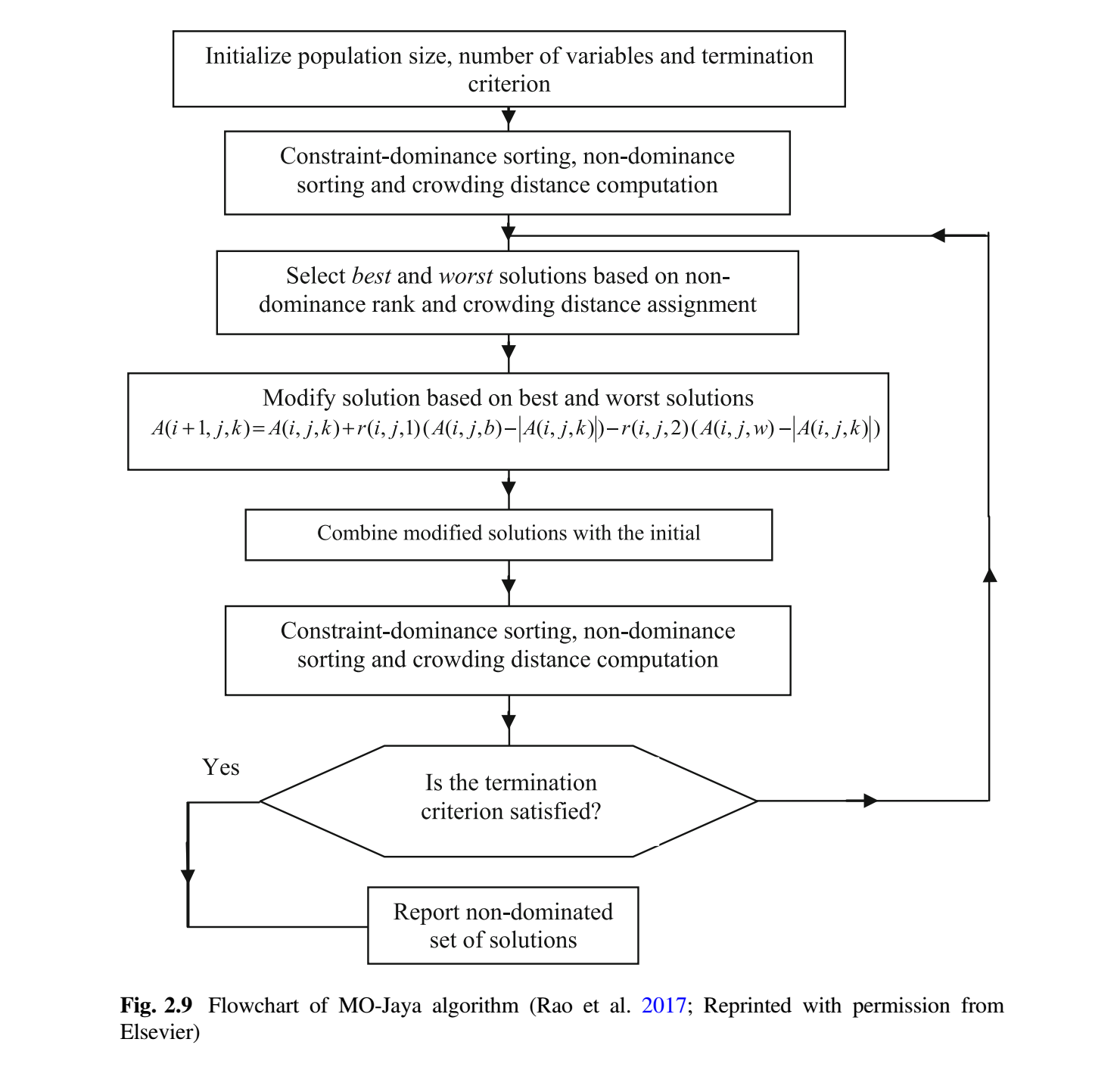
一旦更新了所有的解，更新的解集就会连接到初始种群，以获得 $2NP$ 个解。根据约束-支配概念、非支配概念对这些解重新排序，并计算每个解的拥挤距离值。根据新的排序和拥挤距离值，选择 $NP$ 个好解。根据解的非支配秩和拥挤距离值确定解之间的优越性。秩较高的解被认为优于其他解。如果两个解具有相同的秩，那么拥挤距离值较高的解被认为优于另一个解。图 2.9 给出了 MO-Jaya 算法的流程图。对于每个候选解，MO-Jaya 算法每一代只评估目标函数一次。因此，MO-Jaya 算法所需的函数评估总次数 = 种群规模 $\times$ 迭代次数。但是，当该算法运行多次时，函数评估次数 = 运行次数 $\times$ 种群规模 $\times$ 迭代次数。

约束双目标优化问题的 MO-Jaya 算法演示

让我们考虑车削加工（turning process）中切削参数（cutting
parameters）的双目标优化问题。Yang and Natarajan (2010) 用差分进化和非支配排序遗传算法-II解决了这个问题。该问题有两个目标：最小化刀具磨损 $T_w$ 和最大化金属去除率 $M_r$。目标函数、约束条件和切削参数范围如下。

目标函数：

$$\text{minimize} (T_w) = 0.33349v^{0.1480}f^{0.4912}d^{0.2898} \tag {21}$$

$$\text{maximize} (M_r) = 1000 v f d \tag {22}$$

约束：

  • 温度约束：

$$88.5168 v^{0.3156} f^{0.2856} d^{0.2250} \le 500 \tag {23}$$

  • 表面粗糙度约束：

$$18.5167 v^{0.0757} f^{0.7593} d^{0.1912} \le 2 \tag {24}$$

  • 参数界限：

$$\text{cutting speed (m/min): } 42 \le v \le 201 \tag {25}$$

$$\text{feed rate (mm/rev): } 0.05 \le f\le 0.33 \tag {26}$$

$$\text{depth of cuit (mm): } 0.5 \le d \le 2.5 \tag {27}$$

$v$ = 速度 (米/分钟)；$f$ = 进料 (毫米/转)；$d$ = 切割深度 (毫米)；$M_r$ = 金属去除率 (毫米/分钟)；$T_w$ = 刀具磨损 (毫米)；$T$ = 刀-工界面温度 (°C)；$R_a$ = 表面粗糙度 (微米)。

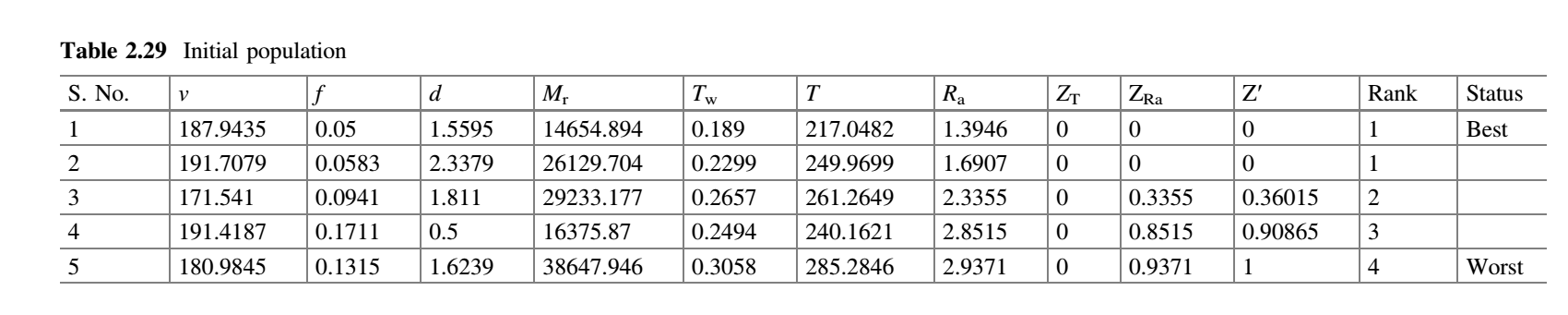
为了演示 MO-Jaya 算法，我们假设种群规模为 5，有三个设计变量 $v$、$f$ 和 $d$ 以及将 1 次迭代作为终止准则。初始种群在变量范围内随机产生，目标函数的相应值见表 2.29。表中显示了 $v$、$f$ 和 $d$ 的均值。

$$(Z_T) _ {max} = 0.000; ; (Z_{R_a}) _ {max} = 0.9371$$

Z’ = 整体约束冲突，可以写成，

$$Z^{‘} = \frac{Z_T}{(Z_T){max}} + \frac{Z{R_a}}{(Z_{R_a}) _ {max}} \tag {28}$$

在表 2.29 中，$Z_T$ 和 $Z_{R_a}$ 下的值表示候选解违背约束值，$(Z_T) _ {max}$ 和 $(Z_{R_a}) _ {max}$ 表示违背刀-工界面温度和表面粗糙度约束的最大值。例如，$(Z_{R_a}) _ {max} = 6.5973 - 2 = 4.5973$。拥挤距离 $CD$ 为 0。如果有更多的约束，则可以将（约束违背程度/$(Z_X) _ {max}$）添加到 $Z^{′}$。这里（$Z_X$）可以是任何约束。

$v$、$f$ 和 $d$ 的随机数 $r_1$ 和 $r_2$ 可以取 0.54 和 0.29；0.48 和 0.37；0.62 和 0.14。用等式 (9) 计算 $v$、$f$ 和 $d$ 的新值。表 2.30 显示了 $v$、$f$ 和 $d$ 的新值以及目标函数的相应值和约束值。

在 NSTLBO 算法和 MO-Jaya 算法的情况下，可以记住以下要点：当所有候选解的 Z′ 值不同时，可以仅基于 Z ′值进行排序，而不需要使用非支配关系和 CD 值进行排序。当候选解的 Z′ 值相同且大于 2 时，只有当候选解的 Z′ 值相同时，候选解的非支配关系才起作用。候选解则可以将非支配概念应用于这些解以对它们进行排序。如果候选解的非支配排序也相同，那么可以计算 CD 值，然后可以进行排序。在利用非支配关系对候选解进行排序时也要记住，有些解可以得到第 1 秩，有些可以得到第 2 秩，有些可以得到第 3 秩等等。然后，CD 度量将用于区分具有相同秩的解。在使用 CD 度量来区分第 1 秩解之后，将区分第 2 秩等等。在此之后，将按照第 1 秩解的 CD 排列解，然后按照第 2 秩解的 CD 排列解，依此类推。

现在将表 2.29 中得到的解与表 2.30 中随机产生的解组合，得到表 2.31。

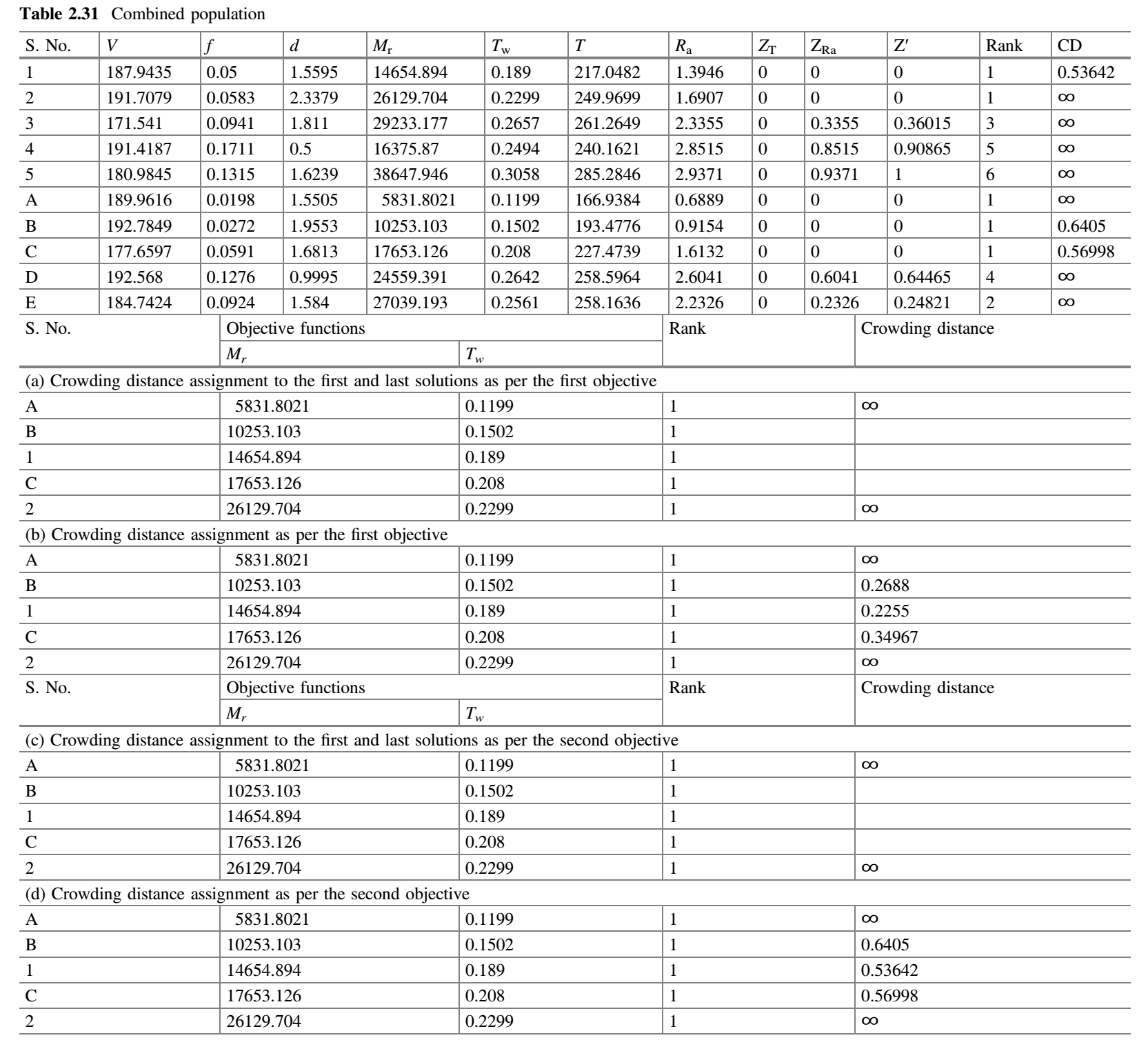
拥挤距离的计算

懒得打公式，只好做成图片的样子

  1. 根据约束-支配和非支配排序概念对表 2.31 的种群进行排序。
  2. 收集所有秩为 1 的解。
  3. 从表 2.31 中确定整个种群的两个目标函数的最小值和最大值，这两个值是：$(M_r) _ {min} = 589.8021$、$(M_r) _ {max} = 52967.946$；$(T_w) _ {min} = 0.1199$、$(T_w) _ {max} = 0.3321$。
  4. 只考虑第一个目标，并按升序对第一个目标函数的所有值进行排序。
    1. 将第一个和最后一个解（即最佳和最差解）的拥挤距离分配为无穷，如表 2.31a 所示。
    2. 拥挤距离 $d_B$、$d_1$ 和 $d_C$ 计算如上图所示。表 2.31b 显示了根据第一个目标分配的拥挤距离。
  5. 只考虑第二个目标，按升序对第二个目标函数值进行排序。
    1. 将第一个和最后一个解（即最佳和最差解）的拥挤距离分配为无穷，如表 2.31c 所示。
    2. 拥挤距离 $d_B$、$d_1$ 和 $d_C$ 计算如下图所示。表 2.31d 显示了根据第二个目标分配的拥挤距离。

懒得打公式，只好做成图片的样子

表 2.32 显示了第一次迭代结束时基于约束支配、非支配排序和拥挤距离的候选解的排列。

在第一次迭代结束时，基于 Z′ 有两个解（第 2 个和第 A 个解）具有的第 1 秩。我们可以用非支配概念来区分这两个解。然而，从这两种解的目标值可以看出，两者都是非支配的。此外，它们的 $CD$ 值是 $\infty$。由于第 2 个和第 A 个解都是第 1 秩的解，这两个解中的任何一个都可以作为下一次迭代的最佳解。第一次迭代结束时的解成为第二次迭代的输入。

多目标拟反向 Jaya（MOQO - Jaya）算法

为了进一步使种群多样化，提高 MO-Jaya 算法的收敛速度，在 MO-Jaya 算法中引入了反向学习的概念。为了获得更好的近似，根据方程 (13) – (15) 生成与当前种群相反的种群，同时两个种群考虑。MOQO-Jaya 算法中的解以类似于 Jaya 算法中的等式 (9) 的方式更新。然而，为了有效和高效地处理多个目标，MOQO-Jaya 算法结合了非支配排序方法和拥挤距离计算机制。

与 MO-Jaya 算法类似，在 MOQO-Jaya 算法中，通过基于非支配概念和拥挤距离值比较分配给解的秩来完成确定最佳解和最差解的任务。首先，随机生成具有 $P$ 个解的初始种群。然后生成与初始种群相结合的拟反向种群。然后基于非支配概念对该组合种群进行排序，并为每个解计算拥挤距离值。然后根据秩和拥挤距离从组合种群中选择 $P$ 个最优解。此外，还根据 Jaya 算法的等式 (9) 更新解。为此，最好和最差的解决方案将被确定。选择秩最高的解作为最佳解。秩最低的解为最差解。如果存在多个相同秩的解，则选择拥挤距离值最高的解作为最佳解，反之亦然。这确保了从搜索空间的稀疏区域中选择最佳解。一旦更新了所有解，更新的解集就会合并到初始群体中。基于非支配概念再次对这些解进行排序，并计算每个解的拥挤距离值。根据新的排序和拥挤距离值选择 $P$ 个好解。基于解的非支配秩和拥挤距离值确定解之间的优越性。秩较高的解被认为优于其他解。如果两个解具有相同的秩，那么拥挤距离值较高的解被认为优于另一个解。MOQO-Jaya 算法所需的函数评估次数 = 种群规模 $\times$ 迭代次数。图 2.10 显示了 MOQO-Jaya 算法的流程图。

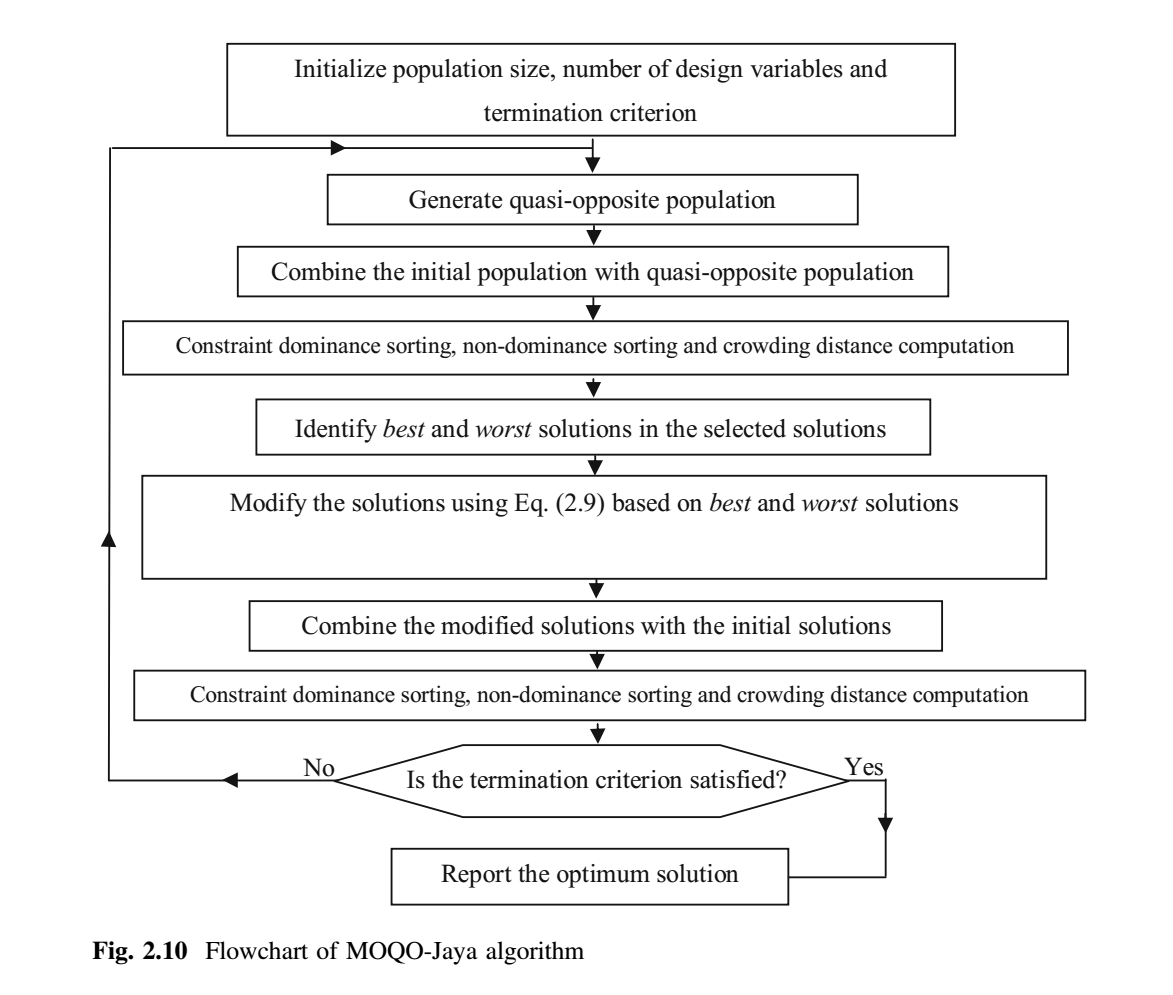
性能评估

采用后验方法求解多目标优化问题的主要目的是获得一组不同的 Pareto 最优解 (Zhou et al. 2011)。因此，为了评估任何多目标优化算法的性能，可以采用三种性能指标，即：

覆盖率（Coverage）

该性能指标比较两组非支配解 (A, B)，并给出一组的个体被另一组的个体支配的百分比。其定义如下：

$$\mathop{\rm Cov}(A, B) = \frac{\vert { b \in B | ; \exists a \in A : a \preceq b } \vert}{\vert B \vert} \tag {29}$$

其中，A 和 B 是比较的两组非支配解，$a \preceq b$ 表示是 a 支配 b 或者等于 b。

Cov (A, B) = 1 表示 B 中的所有点由 A 中的所有点支配或等于 A 中所有的点，$Cov(A, B) = 0$ 表示 B 中的所有解都不被集合 A 覆盖的情况。这里，必须同时考虑 $Cov(A, B)$ 和 $Cov(B, A)$，因为 $Cov(A, B)$ 不一定等于 $1-Cov(B, A)$。当 $Cov(A, B) = 1$、$Cov(B, A) = 0$ 时，A 中的解完全支配 B 中的解（这即 A 的最佳可能性能）。$Cov(A, B)$ 表示 B 中解劣于或等于 A 中的解的百分比；$Cov(B, A)$ 表示 A 解劣于或等于 B 中的解的百分比。

例如，对于最小化类型的双目标优化问题，让非支配集 A 包含以下五个解：a (1.2, 7.8)、b (2.8, 5.1)、 c (4.0, 2.8)、 d (7.0, 2.2) 以及 e (8.4, 1.2)。假设另一个非支配集 B 包含以下解：f (1.3, 8.2)、 g(2.7, 4.9)、 h(3.9, 3.0)、 i(7.3, 2.1) 以及 j(8.2, 1.5)。A 和 B 构成两个 Pareto fronts。然后确定 A 相对于 B 的覆盖率（即，$Cov(A, B)$），遵循以下过程：

首先我们取 a(1.2, 7.8)，并与 f(1.3, 8.2) 进行比较。在这种情况下，a 包含的两个目标的值支配 f 包含的相应值，因此 f 被消除。然后将 a 与 g 进行比较，然后与 h 进行比较，然后依次与 i 和 j 进行比较。可以看出，a 并没有支配 g、h、i 和 j。然后将 b 包含的值与 g、h、i 和 j 进行比较，在这种情况下，g、h、i 和 j 不支配。然后将 c 包含的值与 g、h、i 和 j 进行比较，在这种情况下，g、h、i 和 j 也不支配。同样，d 和 e包含的值与 g、h、i 和 j 进行比较，观察到 g、h、i 和 j 并不支配。f 点没有被考虑，因为它已经被移除了。任何被移除的点都将从集合中消失。因此，在本例中，集合 A 仅支配 B 的 f，因此，$Cov(A, B)$ 为 B 中被支配点的个数与 B 中所有点个数之比，因此 $Cov(A, B) = 1/5 = 0.2$（或 20%）。类似地，可以计算 $Cov(B, A)$，在这种情况下，仅移除 b，因此 $Cov(B, A) = 1/5 = 0.2$（或20%）。在本例中，假设 A 和 B 的点数相等（即 5 个点），但是 A 和 B 的点数可以不同，但是计算覆盖率的过程与本节所述相同。

间距（Spacing）

这种性能指标量化了解的扩散（即，解的均匀分布程度）沿 Pareto 前沿近似。被定义如下：

$$S = \sqrt{\frac{1}{\vert n - 1 \vert} \sum_{i=1}^n (\bar d - d_i)^2} \tag {30}$$

其中，$n$ 是非支配解的数目。

$$d_i = \min _ {i,j \not = j} \sum_{m=1}^k \vert f_m^i - f_m^j \vert , \quad i,j = 1,2, \dots, n \tag {31}$$

其中，$k$ 表示目标个数，$f_m$ 是第 $m$ 个目标的目标函数值。因为在公式 (18) 中不同的目标函数被加在一起，所以归一化目标至关重要。

$$\bar d = \sum_{i=1}^n d_i/ \vert n \vert \tag {32}$$

间距指标决定了 Pareto-front 的平滑度和 Pareto-front 上 Pareto 点分布的均匀性。为此，相邻非支配解的距离方差被计算。$S = 0$ 表示 Pareto 前沿上的所有非支配点等距分布。当 Pareto-fronts 是规则的且包含一组不同的点（没有具有相同目标值的解，即没有重复解）时，间距指标是比较由不同算法获得的 Pareto-fronts 的质量的合适指标。

超体积（Hypervolume）

在多目标优化问题中，超体积（hypervolume，HV）用于比较优化算法获得的Pareto 前沿的质量。HV 给出搜索空间的体积，该体积由特定算法相对于给定参考点获得的 Pareto-front 支配。因此，对于特定算法，HV 的较高值是理想的，这表明了由该算法获得的 Pareto-front 的质量。

在数学上，对于包含 $Q$ 个解的 Pareto-front，对于每个属于 $Q$ 的解 $i$，用参考点 $W$ 和解 $i$ 作为超立方体的对角构造超体积 $v_i$。此后，找到这些超立方体的并集，并按如下公式计算其超体积。

$$HV = \mathop{\rm volume}\Bigl ( \bigcup_{i=1}^{\vert Q \vert} v_i \Bigl) \tag {33}$$

超体积（HV）概念可以通过以下双目标优化示例理解。图 2.11 显示了两个目标 $f_1$ 和 $f_2$ 以及 Pareto-front a-b-c-d-e。

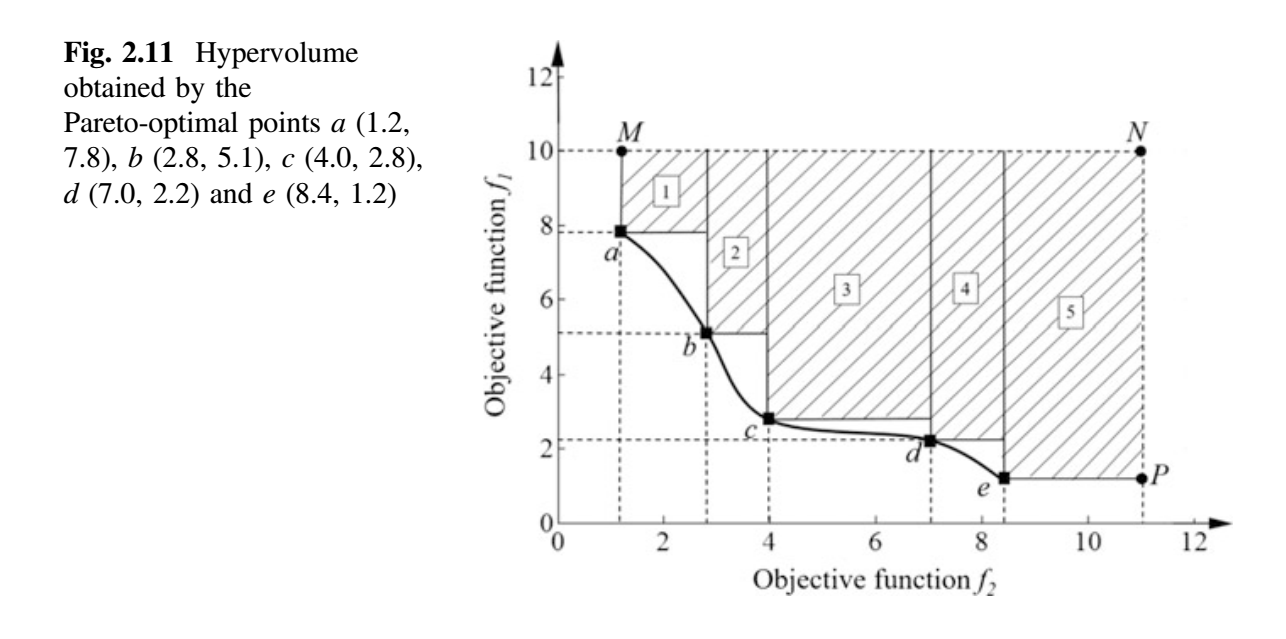
在图 2.11 中，点 a、b、c、d 和 e 是一组非支配点。阴影区域是由 Pareto-front a-b-c-d-e 支配的搜索空间区域，以 $N(11.0, 10.0)$ 为参考点（可以任意选择），超体积计算如下。

$$
\begin{align}
A1 & = ( 2.8 - 1.2 ) \times (10.0 - 7.8) = 3.52 \
A2 & = ( 4.0 - 2.8 ) \times (10.0 - 5.1) = 5.88 \
A3 & = ( 7.0 - 4.0 ) \times (10.0 - 2.8) = 21.60 \
A4 & = ( 8.4 - 7.0 ) \times (10.0 - 2.2) = 10.92 \
A5 & = ( 11 - 8.4 ) \times (10.0 - 1.2) = 22.88 \
HV & = A1 + A2 + A3 + A4 + A5 = 64.80
\end{align}
$$

事实上，如果考虑的是二维图形（2 个目标），那么上面我们计算的是”面积”。如果考虑 3 个目标，那么我们必须计算“体积”。如果考虑的目标超过 3 个，那么我们必须计算“超体积”。可以使用特殊算法来计算超体积 (Beume et al. 2009; Jiang et al. 2015)。

如果任何特定的优化算法产生 Pareto-front f-g-h-i-j（而不是 a-b-c-d-e），那么我们计算 Pareto-front f-g-h-i-j 的超体积，并将该值与 Pareto-front a-b-c-d-e 获得的超体积进行比较，给出更高超体积的优化算法被认为是更好的。超体积给出由特定优化算法获得的 Pareto-front 支配的搜索空间的体积。

参考文献

Beume, N., Fonseca, C. M., Manuel, L.-I., Paquete, L., & Vahrenhold, J. (2009). On the complexity of computing the hypervolume indicator. IEEE Transactions on Evolutionary Computation, 13(5), 1075–1082.

Jiang, S., Zhang, J., Ong, Y.-S., Zhang, A. N., & Tan, P. S. (2015). A simple and fast hypervolume indicator-based multiobjective evolutionary algorithm. IEEE Transactions on Cybernetics, 45 (10), 2202–2213.

Rao, R. V. (2016a). Teaching learning based optimization algorithm and its engineering applications. Switzerland: Springer.

Rao, R. V. (2016b). Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. International Journal of Industrial Engineering Computations, 7, 19–34.

Rao, R. V., & More, K. (2017a). Design optimization and analysis of selected thermal devices using self-adaptive Jayaalgorithm. Energy Conversion and Management, 140, 24–35.

Rao, R. V., & More, K. (2017b). Optimal design and analysis of mechanical draft cooling tower using improved Jaya algorithm. International Journal of Refrigeration. https://doi.org/10.1016/ j.ijrefrig.2017.06.024.

Rao, R. V., & Rai, D. P. (2017a). Optimization of welding processes using quasi oppositional based Jaya algorithm. Journal of Experimental & Theoretical Artificial Intelligence, 29(5), 1099–1117.

Rao, R. V., & Rai, D. P. (2017b). Optimization of submerged arc welding process using quasi-oppositional based Jaya algorithm. Journal of Mechanical Science and Technology, 31(5), 1–10.

Rao, R. V., Rai, D. P., Balic, J. (2016). Multi-objective optimization of machining and micro-machining processes using non-dominated sorting teaching–Learning-based optimiza- tion algorithm. Journal of Intelligent Manufacturing, 2016. https://doi.org/10.1007/s10845- 016-1210-5.

Rao, R. V., Rai, D. P., & Balic, J. (2017). A multi-objective algorithm for optimization of modern machining processes. Engineering Applications of Artificial Intelligence, 61, 103–125.

Rao, R. V., & Saroj, A. (2017). A self-adaptive multi-population based Jaya algorithm for engineering optimization. Swarm and Evolutionary Computation. https://doi.org/10.1016/j. swevo.2017.04.008.

Rao, R. V., & Saroj, A. (2018). An elitism-based self-adaptive multi-population Jaya algorithm and its applications. Soft Computing. https://doi.org/10.1007/s00500-018-3095-z.

Rao, R. V., Savsani, V. J., & Vakharia, D. P. (2011). Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Computer-Aided Design, 43, 303–315. Simon, D. (2013). Evolutionary optimization algorithms. New York: Wiley.

Teo, T. (2006). Exploring dynamic self-adaptive populations in differential evolution. Soft Computing, 10, 673–686.

Yang, S. H., & Natarajan, U. (2010). Multiobjective optimization of cutting parameters in turning process using differential evolution and non-dominated sorting genetic algorithm-II approaches. International Journal of Advanced Manufacturing Technology, 49, 773–784.

Zhou, A., Qu, B.-Y., Li, H., Zhao, S.-Z., Suganthan, P. N., & Zhang, Q. (2011). Multiobjective evolutionary algorithms: a survey of the state of the art. Swarm and Evolutionary Computation, 1(1), 32–49.

本文翻译自：R. Venkata Rao, Jaya: An Advanced Optimization Algorithm and its Engineering Applications

附录：MATLAB 代码

Jaya Code for Unconstrained Rosenbrock Function

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
%% Jaya algorithm
%% Rosenbrock function
function Jaya()
	clc;
	clear all;
	RUNS=30;
	runs=0;
	while(runs<RUNS)
		pop=25; % population size
		var=30; % no. of design variables
		maxFes=500000;
		maxGen=floor(maxFes/pop);
		mini=-30*ones(1,var);
		maxi=30*ones(1,var);
		[row,var]=size(mini);
		x=zeros(pop,var);
		for i=1:var
			x(:,i)=mini(i)+(maxi(i)-mini(i))*rand(pop,1);
		end
		ch=1;
		gen=0;
		f=myobj(x);
		while(gen<maxGen)
			xnew=updatepopulation(x,f);
			xnew=trimr(mini,maxi,xnew);
			fnew=myobj(xnew);
			for i=1:pop
				if(fnew(i)<f(i))
					x(i,:)=xnew(i,:);
					f(i)=fnew(i);
				end
			end
			disp('%%%%%%%% Final population %%%%%%%%%');
			disp([x,f]);
			fnew=[];xnew=[];
			gen=gen+1;
			fopt(gen)=min(f);
		end
		runs=runs+1;
		[val,ind]=min(fopt);
		Fes(runs)=pop*ind;
		best(runs)=val;
	end
	bbest=min(best);
	mbest=mean(best);
	wbest=max(best);
	stdbest=std(best);
	mFes=mean(Fes);
	stdFes=std(Fes);
	fprintf('\n best=%f',bbest);
	fprintf('\n mean=%f',mbest);
	fprintf('\n worst=%f',wbest);
	fprintf('\n std. dev.=%f',stdbest);
	fprintf('\n mean function evaluations=%f',mFes);
end


function[z]=trimr(mini,maxi,x)
	[row,col]=size(x);
	for i=1:col
		x(x(:,i)<mini(i),i)=mini(i);
		x(x(:,i)>maxi(i),i)=maxi(i);
	end
	z=x;
end


function [xnew]=updatepopulation(x,f)
	[row,col]=size(x);
	[t,tindex]=min(f);
	Best=x(tindex,:);
	[w,windex]=max(f);
	worst=x(windex,:);
	xnew=zeros(row,col);
	for i=1:row
		for j=1:col
			r=rand(1,2);
			xnew(i,j)=x(i,j)+r(1)*(Best(j)-abs(x(i,j)))-r(2)*(worst(j)-abs(x(i,j)));
		end
	end
end


function [f]=myobj(x)
	[r,c]=size(x);
	for i=1:r
		y=0;
		for j=1:c-1
			y=y+(100*(x(i,j)^2-x(i,j+1))^2+(1-x(i,j))^2);
		end
		z(i)=y;
	end
	f=z';
end

Jaya Code for Constrained Himmelblau Function

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
%% Jaya algorithm
%% Constrained optimization
%% Himmelblau function
function Jaya()
	clc;
	clear all;
	RUNS=10;
	runs=0;
	while(runs<RUNS)
		pop=5; % population size
		var=2; % no. of design variables
		maxFes=150000;
		maxGen=floor(maxFes/pop);
		mini=[-5 -5];
		maxi=[5 5];
		[row,var]=size(mini);
		x=zeros(pop,var);
		for i=1:var
			x(:,i)=mini(i)+(maxi(i)-mini(i))*rand(pop,1);
		end
		ch=1;
		gen=0;
		f=myobj(x);
		while(gen<maxGen)
			xnew=updatepopulation(x,f);
			xnew=trimr(mini,maxi,xnew);
			fnew=myobj(xnew);
			for i=1:pop
				if(fnew(i)<f(i))
					x(i,:)=xnew(i,:);
					f(i)=fnew(i);
				end
			end
			disp('%%%%%% Final population%%%%%%%');
			disp([x,f]);
			fnew=[];xnew=[];
			gen=gen+1;
			fopt(gen)=min(f);
		end
		runs=runs+1;
		[val,ind]=min(fopt);
		Fes(runs)=pop*ind;
		best(runs)=val;
	end
	bbest=min(best);
	mbest=mean(best);
	wbest=max(best);
	stdbest=std(best);
	mFes=mean(Fes);
	fprintf('\n best=%f',bbest);
	fprintf('\n mean=%f',mbest);
	fprintf('\n worst=%f',wbest);
	fprintf('\n std. dev.=%f',stdbest);
	fprintf('\n mean Fes=%f',mFes);
end


function[z]=trimr(mini,maxi,x)
	[row,col]=size(x);
	for i=1:col
		x(x(:,i)<mini(i),i)=mini(i);
		x(x(:,i)>maxi(i),i)=maxi(i);
	end
	z=x;
end


function [xnew]=updatepopulation(x,f)
	[row,col]=size(x);
	[t,tindex]=min(f);
	Best=x(tindex,:);
	[w,windex]=max(f);
	worst=x(windex,:);
	xnew=zeros(row,col);
	for i=1:row
		for j=1:col
			r=rand(1,2);
			xnew(i,j)=x(i,j)+r(1)*(Best(j)-abs(x(i,j)))-r(2)*(worst(j)-abs(x(i,j)));
		end
	end
end


function [f]=myobj(x)
	[r,c]=size(x);
	Z=zeros(r,1);
	for i=1:r
		x1=x(i,1);
		x2=x(i,2);
		z=(((x1^2)+x2-11)^2)+((x1+x2^2-7)^2);
		g1=26-((x1-5)^2)-((x2)^2);
		g2=20-(4*x1)-x2;
		p1=10*((min(0,g1))^2); % penalty if constraint 1 is violated
		p2=10*((min(0,g2))^2); % penalty if constraint 2 is violated
		Z(i)=z+p1+p2; % penalized objective function value
	end
	f=Z;
end;

SAMPE Jaya Code for Unconstrained Himmelblau Function

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
%% Algorithm_MP_ES
clc
clear all
funev=150000; % Maximum functionevaluations
IDR=1;
format shortg
%NP = input('Enter the population size:');
NP=25; % Population size
ES=2; % Elite size
NMP=2 ;% Number of multi population initial
NG=funev/NP; % Maximum number of generations
DV=2; % Number of design variables
% NG = input('Enter the no of generation :');
% DV = input('Enter the no of Decision variable:');
for m=1:IDR % No. of Independent run
	for j = 1:DV
		DV_min(j)=[-5];
		DV_max(j)=[5];
	end
	% Initial Population Generation
	for i=1:NP
		for j = 1 : DV
			x(i,j) = DV_min(j) + (DV_max(j) - DV_min(j))*rand(1);
		end
	end
	for i = 1 : NP
		x(i,DV + 1) = objective(x(i,:));
	end
	% start of generation
	for k=1:NG
		x=unique(x, 'rows');
		[r,c]= size(x);
		if r<NP % If current population size is less than NP add NP-r %populations
			for i=r+1:NP
				for j = 1:DV
					x(i,j) = DV_min(j) + (DV_max(j) - DV_min(j))*rand(1);
				end
			end
			for i = r+1:NP
				x(i,DV + 1) = objective(x(i,:));
			end
		else
			x(:,:)=x(:,:);
		end
		%% Replace the worst solution with elite solutions
		x=sortrows(x,DV+1); % sort the solutions in ascending order
		x(NP-ES+1:NP,:)= x(1:ES,:);
		[f_min,ind_min] = min(x(:,DV+1));
		[f_max,ind_max] = max(x(:,DV+1));
		%% Devide population and modify the solutions
		x1=[];
		for n=1:NMP
			a=round((n-1)*NP/NMP)+1;
			b=round(NP/NMP*n);
			if b>NP
				for i=NP+1:b
					for j=1:DV
						x(i,j)= randsample(x(:,j),1);
					end
					x(i,DV + 1) = objective(x(i,:));
				end
			end
			for i=a:b
				for j=1:DV
					x1(i,j) = x(i,j) +rand*(x(a,j)- abs(x(i,j)))-rand*(x(b,j)- abs(x(i,j)));
				end
			end
		end
		% Check for the bounds of decision variable
		for i=1:NP
			for j=1:DV
				if x1(i,j)<DV_min(j)
					x1(i,j)= DV_min(j);
				elseif x1(i,j)>DV_max(j)
					x1(i,j) = DV_max(j);
				else
					x1(i,j) = x1(i,j);
				end
			end
		end
		for i = 1 : NP
			x1(i,DV + 1) = objective(x1(i,:));
		end
		for i=1:NP
			if x(i,DV + 1)< x1(i,DV + 1)
				x(i,DV + 1)= x(i,DV + 1);
				for j=1:DV+1
					x(i,j) = x(i,j);
				end
			else
				x(i,DV + 1)= x1(i,DV + 1);
				for j=1:DV+1
					x(i,j) = x1(i,j);
				end
			end
		end
		[f_best(k),l2] = min(x(:,DV+1));
		for j=1:DV
			x_fi(j)= x(l2,j);
		end
		% self-adaptive population concept starts over here
		if (f_min<f_best(k))
			NMP=NMP+1;
			if (NP/NMP)>=3
				NMP=NMP;
			else
				NMP=NMP-1;
			end
		else
			if NMP>1
				NMP= NMP-1;
			else
				NMP=1;
			end
		end
		np(k)=NMP;
		% disp(NMP)
		% self-adaptive populations concept ends over
	end
	disp(['--------[ ','Run No.= ',num2str(m), ' ]--------'])
	disp(['Optimum value =',num2str(min(f_best),30)])
	disp(['DV: ',num2str(x_fi,7)])
	fprintf('\n \n');
	[f_min1(m),ind1(m)]= min(f_best);
	f_max1(m)= max(f_best);
end
Best= min(f_min1);
Worst=max(f_min1);
Mean = mean(f_min1);
SD = std(f_min1);
MFE= mean(ind1)*NP;
fprintf('\n Best=%f',Best);
fprintf('\n Worst=%f',Worst);
fprintf('\n Mean=%f',Mean);
fprintf('\n SD=%f', SD);
fprintf('\n MFE=%f', MFE);
fprintf('\n FE=%f',funev);
fprintf('\n \n');

1
2
3
4
5
6
7
8
function [ Z ] = objective( x )
	% Unconstrained optimization
	% Himmelblau function
	% Detailed explanation goes here
	x1=x(1);
	x2=x(2);
	Z=(((x1^2)+x2-11)^2)+((x1+x2^2-7)^2);
end

SAMPE Jaya Code for Constrained Himmelblau Function

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
%% Algorithm_MP_ES
clc
clear all
funev=150000; % Maximum function evaluations
IDR=1;
format shortg
%NP = input('Enter the population size:');
NP=25; % Population size
ES=2; % Elite size
NMP=2 ;% Number of multi population initial
NG=funev/NP; % Maximum number of generations
DV=2; % Number of design variables
% NG = input('Enter the no of generation :');
% DV = input('Enter the no of Decision variable:');
for m=1:IDR % No. of Independent run
	for j = 1 : DV
		DV_min(j)=[-5];
		DV_max(j)=[5];
	end
	% Initial Population Generation
	for i=1:NP
		for j = 1 : DV
			x(i,j) = DV_min(j) + (DV_max(j) - DV_min(j))*rand(1);
		end
	end
	for i = 1 : NP
		x(i,DV + 1) = objective(x(i,:));
	end
	% start of generation
	for k=1:NG
		x=unique(x, 'rows');
		[r,c]= size(x);
		if r<NP % If current population size is less than NP add NP-r %populations
			for i=r+1:NP
				for j = 1 : DV
					x(i,j) = DV_min(j) + (DV_max(j) - DV_min(j))*rand(1);
				end
			end
			for i = r+1:NP
				x(i,DV + 1) = objective(x(i,:));
			end
		else
			x(:,:)=x(:,:);
		end
		%% Replace the worst solution with elite solutions
		x=sortrows(x,DV+1); % sort the solutions in ascending order
		x(NP-ES+1:NP,:)= x(1:ES,:);
		[f_min,ind_min] = min(x(:,DV+1));
		[f_max,ind_max] = max(x(:,DV+1));
		%% Devide population and modify the solutions
		x1=[];
		for n=1:NMP
			a=round((n-1)*NP/NMP)+1;
			b=round(NP/NMP*n);
			if b>NP
				for i=NP+1:b
					for j=1:DV
						x(i,j)= randsample(x(:,j),1);
					end
					x(i,DV + 1) = objective(x(i,:));
				end
			end
			for i=a:b
				for j=1:DV
					x1(i,j) = x(i,j) +rand*(x(a,j)- abs(x(i,j)))-rand*(x(b,j)- abs(x(i,j)));
				end
			end
		end
		% Check for the bounds of decision variable
		for i=1:NP
			for j=1:DV
				if x1(i,j)<DV_min(j)
					x1(i,j)= DV_min(j);
				elseif x1(i,j)>DV_max(j)
					x1(i,j) = DV_max(j);
				else
					x1(i,j) = x1(i,j);
				end
			end
		end
		for i = 1:NP
			x1(i,DV + 1) = objective(x1(i,:));
		end
		for i=1:NP
			if x(i,DV + 1)< x1(i,DV + 1)
				x(i,DV + 1)= x(i,DV + 1);
				for j=1:DV+1
					x(i,j) = x(i,j);
				end
			else
				x(i,DV + 1)= x1(i,DV + 1);
				for j=1:DV+1
					x(i,j) = x1(i,j);
				end
			end
		end
		[f_best(k),l2] = min(x(:,DV+1));
		for j=1:DV
			x_fi(j)= x(l2,j);
		end
		%% self-adaptive population concept startsover here
		if (f_min<f_best(k))
			NMP=NMP+1;
			if (NP/NMP)>=3
				NMP=NMP;
			else
				NMP=NMP-1;
			end
		else
			if NMP>1
				NMP= NMP-1;
			else
				NMP=1;
			end
		end
		np(k)=NMP;
		% disp(NMP)
		% self-adaptive populations concept ends over here
	end
	disp(['--------[ ','Run No.= ',num2str(m), ' ]--------'])
	disp(['Optimum value =',num2str(min(f_best),30)])
	disp(['DV: ',num2str(x_fi,7)])
	fprintf('\n \n');
	[f_min1(m),ind1(m)]= min(f_best);
	f_max1(m)= max(f_best);
end
Best= min(f_min1);
Worst=max(f_min1);
Mean = mean(f_min1);
SD = std(f_min1);
MFE= mean(ind1)*NP;
fprintf('\n Best=%f',Best);
fprintf('\n Worst=%f',Worst);
fprintf('\n Mean=%f',Mean);
fprintf('\n SD=%f', SD);
fprintf('\n MFE=%f', MFE);
fprintf('\n FE=%f',funev);
fprintf('\n \n');
1
2
3
4
5
6
7
8
9
10
11
12
13
14
%%%%%%%%%%%%%%%% objective%%%%%%%%%%%%%%%%%%
function [Z] = objective(x)
% Constrained optimization
% Himmelblau function
% Detailed explanation goes here
x1=x(1);
x2=x(2);
z=(((x1^2)+x2-11)^2)+((x1+x2^2-7)^2);
g1=26-((x1-5)^2)-((x2)^2);
g2=20-(4*x1)-x2;
p1=10*((min(0,g1))^2); % penalty if constraint 1 is violated
p2=10*((min(0,g2))^2); % penalty if constraint 2 is violated
Z=z+p1+p2; % penalized objective function value
end

MOQO Jaya Code for ECM Process

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
function [z]=moqojaya()
    RUNS=0;
    maxRUNS=1;
    while(RUNS<maxRUNS)
        clearvars -except maxRUNS RUNS;
        clc;
        FEs=0;
        maxFEs=3750;
        gen=0;
        temp_cl=[];
        pop=50;
        sch=[0 0 1];
        mini=[8 300 3];
        maxi=[200 5000 21];
        dim=numel(mini);
        n=numel(sch);
        for i=1:dim
            cl(:,i)=mini(i)+(maxi(i)-mini(i))*rand(pop,1);
        end
        cl_new=quasi(mini,maxi,cl);
        cl=[cl;cl_new];
        cl(:,dim+1:dim+n)=myobj(cl);
        temp_cl=cl;
        cl=[];
        b=[];
        cl=NS(n,dim,temp_cl,sch);
        cl=cl(1:pop,:);
        temp_cl=[];
    while(FEs<=maxFEs)
        a=[]; b=[]; a= cl(:,dim+n+1)==1; b=find(cl(a,dim+n+2)==100); count=numel(b);
        temp_cl=updation(cl(:,1:dim),count);
        temp_cl=trimr(mini,maxi,temp_cl);
        temp_cl(:,dim+1:dim+n)=myobj(temp_cl);
        comb_cl=cat(1,cl(:,1:dim+n),temp_cl);
        temp_cl=[];
        cl=[];
        cl=NS(n,dim,comb_cl,sch);
        cl=cl(1:pop,:);
        comb_cl=[];
        FEs=FEs+pop;
        temp_cl=quasi(mini,maxi,cl(:,1:dim));
        temp_cl(:,dim+1:dim+n)=myobj(temp_cl);
        comb_cl=cat(1,cl(:,1:dim+n),temp_cl);
        temp_cl=[];
        cl=[];
        cl=NS(n,dim,comb_cl,sch);
        cl=cl(1:pop,:);
        comb_cl=[];
        cl=cat(2,cl,constraint(cl(:,1:dim)));
        FEs=FEs+pop;
        disp(FEs);
        plot3(cl(:,dim+1),cl(:,dim+2),cl(:,dim+3),'*');
        xlabel('Z1');
        ylabel('Z2');
        zlabel('Z3');
        gen=gen+1;
        disp(gen);
        figure(1);
        end
        RUNS=RUNS+1;
    end
end


function [z1]= NS(n,dim,cl,sch)
	[pop,col]=size(cl);
	x=cl(:,1:dim);
	func=cl(:,dim+1:dim+n);
	f=func;
	srn=[1:pop];
	cons=constraint(x);
	tempf=f;
	[p,c]=size(f);
	l=1;
	rank=1;
	score=[];
	tscore=zeros(1,2);
	nd=[];
	todel=[];
	index=[];
	t=[];
	while(p>1)
		for i=1:p
			win=1;
			for j=1:p
				if(i ~= j)
					if(cons(i)<cons(j))
						win=win+1;
					end
					if(cons(i)>cons(j))
						break;
					end
					if(cons(i)==cons(j))
						for k=1:n
							switch sch(k)
								case 0
									if(f(i,k)<f(j,k))
										score(1,k)=1;
										score(2,k)=0;
									end
									if(f(i,k)==f(j,k))
										score(1,k)=0;
										score(2,k)=0;
									end
									if(f(i,k)>f(j,k))
										score(1,k)=0;
										score(2,k)=1;
									end
								case 1
									if(f(i,k)>f(j,k))
										score(1,k)=1;
										score(2,k)=0;
									end
									if(f(i,k)==f(j,k))
										score(1,k)=0;
										score(2,k)=0;
									end
									if(f(i,k)<f(j,k))
										score(1,k)=0;
										score(2,k)=1;
									end
							end
						end
						tscore(1)=sum(score(1,:));
						tscore(2)=sum(score(2,:));
						if(tscore(1)>0.0 && tscore(1)<=n)
							win=win+1;
						end
					end
				end
			end
			if(win==p)
				nd(l)=srn(i);
				todel(l)=i;
				l=l+1;
			end
			score=[];
			tscore=zeros(1,2);
		end
		if(numel(nd)==0)
			tempf(srn,n+1)=rank;
			rank=rank+1;
			f=[];
			srn=[];
			cons=[];
		else
			tempf(nd,n+1)=rank;
			rank=rank+1;
			f(todel,:)=[];
			srn(todel)=[];
			cons(todel)=[];
		end
		nd=[];
		todel=[];
		l=1;
		[p,c]=size(f);
	end
	tempf(tempf(:,n+1)==0,n+1)=rank;
	x=cat(2,x,tempf);
	[t,index]=sort(tempf(:,n+1),'ascend');
	x=x(index,:);
	%disp(x);
	for i=1:n
		fmin(i)=min(x(:,dim+i));
		fmax(i)=max(x(:,dim+i));
	end
	r=max(x(:,dim+n+1));
	%disp(r);
	for k=1:r
		t=[];
		index=[];
		f2=x(x(:,dim+n+1)==k,dim+1:dim+n);
		[row,col]=size(f2);
		if(row<2)
			x(x(:,dim+n+1)==k,dim+n+2)=100;
		else
			x(x(:,dim+n+1)==k,dim+n+2)=crowdist(fmin,fmax,f2);
			x1=x(x(:,dim+n+1)==k,:);
			[t,index]=sort(x1(:,dim+n+2),'descend');
			x1=x1(index,:);
			x(x(:,dim+n+1)==k,:)=x1;
		end
	end
	z1=x;
end


function [d]=crowdist(fmin,fmax,f)
	[row,col]=size(f);
	d=zeros(row,1);
	for i=1:col
		[I,t]=sort(f(:,i));
		%disp(t);
		d(t(1))=100;
		d(t(row))=100;
		for j=2:row-1
			d(t(j))=d(t(j))+(f(t(j+1),i)-f(t(j-1),i))/(fmax(i)-fmin(i));
		end
	end
	d(d>100)=100;
end


function [z2]=updation(temp_cl,count)
	[row,col]=size(temp_cl);
	best=temp_cl(round(count-(count-1)*rand(1,1)),:);
	worst=temp_cl(end,:);
	for j=1:row
		for i=1:col
			rn=rand(1,2);
			temp_cl(j,i)=temp_cl(j,i)+rn(1)*(best(i)-abs(temp_cl(j,i)))-rn(2)*(worst(i)-abs(temp_cl(j,i)));
		end
	end
	z2=temp_cl;
end


function[z4]=trimr(mini,maxi,temp)
	[row,col]=size(temp);
	for i=1:col
		temp(temp(:,i)<mini(i),i)=mini(i);
		temp(temp(:,i)>maxi(i),i)=maxi(i);
	end
	z4=temp;
end


function [f1]=myobj(x)
	[row,col]=size(x);
	for i=1:row
		f=x(i,1);
		U=x(i,2);
		V=x(i,3);
		Z1=(f^0.381067)*(U^-0.372623)*(V^3.155414)*exp(-3.128926);
		Z2 = (f^3.528345)*(U^0.000742)*(V^-2.52255)*exp(0.391436);
		Z3=f;
		f1(i,1)=Z1;
		f1(i,2)=Z2;
		f1(i,3)=Z3;
	end
end


function[z5]=constraint(x)
	[row,col]=size(x);
	for i=1:row
		f=x(i,1);
		U=x(i,2);
		V=x(i,3);
		g1=(1-(f^2.133007)*(U^-1.088937)*(V^-0.351436)*exp(0.321968));
		g2=((f^-0.844369)*(U^-2.526075)*(V^1.546257)*exp(12.57697))-1;
		g3=1-((f^0.075213)*(U^-2.488362)*(V^0.240542)*exp(11.75651));
		G1(i,1)=min(0,g1);
		G2(i,1)=min(0,g2);
		G3(i,1)=min(0,g3);
	end
	G1str=max(abs(G1));
	G2str=max(abs(G2));
	G3str=max(abs(G3));
	if(max(abs(G1))==0)
		G1str=1;
	end
	if(max(abs(G2))==0)
		G2str=1;
	end
	if(max(abs(G3))==0)
		G3str=1;
	end
	z5=(abs(G1)/G1str)+(abs(G2)/G2str)+(abs(G3)/G3str);
end


function [Pnew]=quasi(mini,maxi,P)
	[row,col]=size(P);
	mini=repmat(mini,row,1);
	maxi=repmat(maxi,row,1);
	A=0.5*(mini+maxi);
	B=((mini+maxi)-P);
	Pnew=A+(B-A).*rand(row,col);
end