经典CS问题Python实现：简单问题

发表于 更新于 分类于 阅读次数：

首先，我们将探索一些简单的问题，这些问题可以用几个相对较短的函数来解决。

斐波那契数列

斐波那契数列是一系列的数字，除了第一个和第二个之外的任何数字都是其前两个数之和：

0, 1, 1, 2, 3, 5, 8, 13, 21, …

序列中第一个斐波那契数的值是0。第四个斐波那契数的值是2。因此，要得到序列中任意斐波那契数n的值，可以使用以下公式

1
fib(n) = fib(n - 1) + fib(n - 2)

第一次递归尝试

上述计算斐波那契数列中值的公式是一种伪代码形式，可以简单地转换成 Python 递归函数（递归函数是自我调用的函数）。这种机械转换将作为我们编写斐波那契数列的第一次尝试。

程序清单1 fib1.py

1
2
3
4
5
6
def fib1(n: int) -> int:
	return fib1(n - 1) + fib1(n - 2)


if __name__ == "__main__":
	print(fib1(5))

如果我们尝试运行 fib1.py，程序会产生错误：

1
RecursionError: maximum recursion depth exceeded

其结果是 fib(1) 将一直运行下去，而不返回最终结果。每次调用 fib1() 都会导致另外两次调用 fib1() 而不会结束。我们将这种情况称为无限递归（infinite recursion），如图1所示，这类似于无限循环。

利用初始条件

值得注意的是，在运行 fib1() 之前，Python 环境没有任何迹象表明它存在问题。程序员有责任避免无限递归，而不是依靠编译器或解释器。无限递归的原因是我们未指定初始条件。在递归函数中，将初始条件作为停止点。

在斐波那契函数的情况下，序列的前两个值（0，1）是特殊情况，它们都不是它们之前两个值之和。让我们将它们作为初始条件。

程序清单2 fib2.py

1
2
3
4
5
6
7
8
9
def fib2(n: int) -> int:
	if n < 2:    # base case
		return n
	return fib2(n - 1) + fib2(n - 2)    # recursive case


if __name__ == '__main__':
	print(fib2(5))
	print(fib2(10))

尝试使用一些小值，可以成功调用 fib2() 并返回正确的结果。

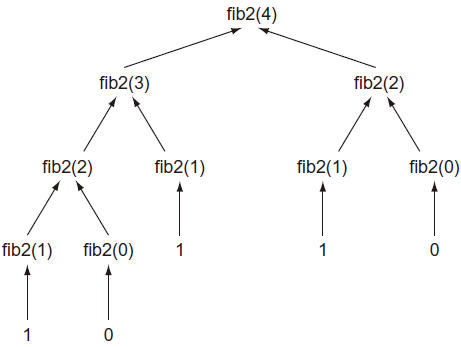
不要试着调用 fib2(50)，执行永远不会完成！为什么？如图2所示，每次调用 fib2() 都会通过递归调用 fib2(n - 1) 和 fib2(n - 2) 产生2个另外 fib2() 调用。换句话说，调用树呈指数增长。例如，调用 fib2(4) 会产生：

1
2
3
4
5
6
7
8
9
10
fib2(4) -> fib2(3), fib2(2)
fib2(3) -> fib2(2), fib2(1)
fib2(2) -> fib2(1), fib2(0)
fib2(2) -> fib2(1), fib2(0)

fib2(1) -> 1
fib2(1) -> 1
fib2(1) -> 1
fib2(0) -> 0
fib2(0) -> 0

如果计算（在代码中添加一些 print 调用），你会发现，仅仅为了计算第4个元素就需要9次调用！计算第5个元素需要15次调用，计算第10个元素需要177次调用，计算第20元素需要21,891次调用。程序需要优化。

记忆化拯救世界

记忆化（memoization）是一种在计算完成后，存储计算结果的技术。这样当再次需要它们时，仅需要查找它们，而不是二次（或成百上千次）计算它们。

让我们利用 Python 字典来实现记忆化，以创建新的斐波那契函数。

程序清单3 fib3.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from typing import Dict


memo: Dict[int, int] = {0: 0, 1: 1}    # base cases

def fib3(n: int) -> int:
    if n not in memo:
        memo[n] = fib3(n - 1) + fib3(n - 2)    # memoization
    return memo[n]


if __name__ == '__main__':
    print(fib3(5))
    print(fib3(50))

现在，可以安全地调用 fib3(50) 了。调用 fib3(20) 只会导致 fib3() 被调用39次，而调用 fib2(20 ) 会导致 fib2() 调用21891次。memo 中预先填充了0和1的初始条件，从而避免了复杂的 if 语句。

自动记忆化

fib3() 可以进一步简化。Python 有一个内置装饰器，可以自动记忆任何函数。在 fib4() 中，除了使用了装饰器 @functools.lru_cache()，其他的代码与 fib2() 中的完全相同。每次使用新参数执行 fib4() 时，装饰器都会缓存返回值。之后使用相同参数调用 fib4() 时，将从缓存中取出该参数之前的返回值。

程序清单4 fib4.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from functools import lru_cache


@lru_cache(maxsize=None)
def fib4(n: int) -> int:    # same definition as fib2()
    if n < 2: # base case
        return n
    return fib4(n - 2) + fib4(n - 1) # recursive case


if __name__ == '__main__':
    print(fib4(5))
    print(fib4(50))

请注意，我们能够立即计算出 fib4(50)，即使函数的主体与 fib2() 中的相同。@lru_cache 的 maxsize 属性表示，缓存它正在装饰的函数的调用次数。将其设置为 None 表示没有限制。

继续简化

还有一个更高性能的选择，即，用老式的迭代方法解决斐波纳契问题。

程序清单5 fib5.py

1
2
3
4
5
6
7
8
9
10
11
12
13
def fib5(n: int) -> int:
    if n == 0: return 0    # special case
    last: int = 0    # initially set to fib(0)
    next: int = 1    # initially set to fib(1)
    for _ in range(1, n):
        last, next = next, last + next
    return next


if __name__ == '__main__':
    print(fib5(5))
    print(fib5(50))

警告 fib5() 中 for 循环的主体使用元组拆包（tuple unpack）的方式可能有点过于讨巧。有些人可能会觉得它为了简洁而牺牲了可读性，其他一些人则可能会认为简洁本身更具可读性。要点是，last 被设置为 next 的前一个值，next 被设置为 last 的前一个值加上 next 的前一个值。这避免了创建临时变量来保存更新过程中的旧值。在 Python 中，以这种方式对某种变量交换使用元组拆包是很常见的。

使用这种方法，for 循环的主体将最多运行n - 1次。换句话说，这是迄今为止最高效版本。对于第20个元素，fib5() 需要19次调用，而 fib2() 需要21891次调用。这可能会对实际应用产生重大影响！

在递归解中，我们自顶向下工作。在这个迭代解中，我们自底向上工作。有时候递归是最直观的方法。举个例子，fib1() 和 fib2() 的核心是对原始斐波那契公式的机械转换。然而，朴素的递归解也会带来巨大的性能损失。需要记住的是，任何可以递归解决的问题也可以迭代解决。

何不试一下生成器？

到目前为止，我们已经编写了在斐波那契数列中输出单个值的函数。如果我们想要输出整个序列直到某个值呢？使用 yield 语句很容易将 fib5() 转换成 Python 生成器。当生成器被迭代时，每次迭代都会使用 yield 语句从斐波那契序列中输出一个值。

程序清单6 fib6.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from typing import Generator


def fib6(n: int) -> Generator[int, None, None]:
    yield 0    # special case
    if n > 0: yield 1    # special case
    last: int = 0    # initially set to fib(1)
    next: int = 1    # initially set to fib(2)
    for _ in range(1, n):
        last, next = next, last + next
        yield next


if __name__ == '__main__':
    for i in fib6(50):
        print(i)

如果你运行 fib6.py，你会看到斐波纳契数列中有51个值被打印出来。

琐碎的压缩

节省空间（虚拟或真实）通常很重要。使用更少的空间更有效率，而且可以省钱。如果你租的公寓比你东西占用和家庭需要的大，你可以考虑“降级”到小一点、便宜点的地方。如果你的数据是按文件大小付费，存储在服务器上，你可能希望压缩它，以降低存储成本。压缩是以占用较少空间的方式获取数据并对其进行编码（改变其形式）的行为。解压是反向过程，将数据返回到其原始形式。

如果压缩数据更节省存储空间，那么为什么不压缩所有数据呢？这里存在时间和空间之间权衡。压缩一段数据并将其解压回原始形式需要时间。因此，数据压缩只有在体积小优先于执行快的情况下才有意义。想象一下通过网络传输的大文件，压缩是有意义的，因为传输文件的时间要比接收后解压文件的时间长。此外，压缩文件以存储在原始服务器上所花费的时间只需计算一次。

当你意识到数据存储类型使用的位比其内容严格要求的位多时，最简单的数据压缩就成功了。例如，从底层来看，如果将一个永远不会超过65535（2^16 - 1）的无符号整数作为64位无符号整数存储在内存中，那么它的存储效率就很低。它可以存储为16位无符号整数，且空间消耗减少75%。如果存储数百万个这样的数，那么浪费的空间将达到数兆字节（megabytes）。

在 Python 中，为了简单起见，开发人员从位（bits）思考的角度被屏蔽。没有64位无符号整型，也没有16位无符号整型。只有一个 int 类型可以存储任意精度的数字。函数 sys.getsizeof() 可以助你找出 Python 对象消耗了多少字节的内存。但是由于 Python 对象系统固有的开销，在 Python 3.7 中没有办法创建占用少于28字节（ 224位）的 int 类型。一个 int 可以一次扩展一比特，但是它至少消耗28个字节。

注意 如果你对二进制有点生疏，可以回想一下，一比特是一个1或0。二进制以2为底，用0、1序列来表示一个数字。在本节中，你不需要用二进制做任何数学运算，但是你需要理解一个类型存储的位数决定了它可以代表多少不同的值。例如，1位可以代表2个值（0或1），2位可以代表4个值（00、01、10或11），3位可以代表8个值，依此类推。

如果一个类型要表示的所有可能的值的数量少于用于存储它的位数可以表示值的数量，则它可以被更有效地存储。考虑在DNA形成基因的核苷酸。每个核苷酸只能是四个值（A、C、G或T）中的一个。然而，如果基因以 str 类型存储，可以认为其是 Unicode 字符集，每个核苷酸将由一个字符表示，这通常需要8位存储空间。在二进制中，只需2位就可以表示4个不同的值（即00、01、10和11）。如果把A分配给00，把C分配给01，把G分配给10，把T分配给11，核苷酸“字符串”所需的存储量可以减少75%（每核苷酸从8位减少到2位）。

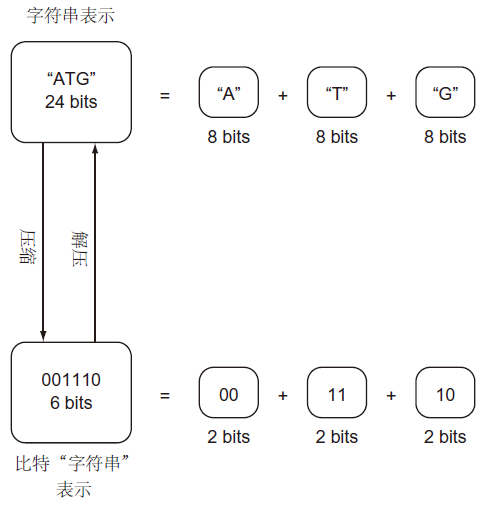
如图4所示，将核苷酸存储为比特“字符串”，而不是存储为 str。比特“字符串”就是它听起来的样子：任意长度的0、1序列。不幸的是，Python 标准库不包含用于处理任意长度的比特“字符串”的现成构造。下面的代码将由A、C、G和T组成的字符串转换成比特“字符串”，然后再转换回来。比特“字符串”存储在 int 中。因为 Python 中的 int 类型可以是任意长度，所以它可以用作任意长度的比特“字符串”。为了转换回字符串，我们将实现 Python的 __str__()特殊方法。

程序清单7 trivial_compression.py

1
2
3
4
class CompressedGene:
    def __init__(self, gene: str) -> None:
        self._compress(gene)

CompressedGene 提供了 str 类型代表基因中核苷酸序列，它在内部将核苷酸序列存储为比特字符串。__init __() 方法的主要作用是使用适当的数据初始化比特“字符串”构造。__init __() 调用 _compress() 来执行实际上将核苷酸 str 转换为比特“字符串”的脏工作（dirty work）。

请注意 _compress() 以下划线开头。Python 中没有真正私有方法或变量的概念。所有变量和方法都可以通过反射来访问，没有严格的隐私保护措施。前导下划线用作约定，表示不应该依赖类外部的actor实现方法。

提示 如果使用两个前导下划线在类中开始一个方法或实例变量名，Python 会对它进行“命名破坏”，加盐（salt）以改变它的实现名称，使它不容易被其他类发现。在这里，我们用一个下划线来表示一个“私有”变量或方法，但是如果你真的想强调是某个变量或方法是私有的，则可以用两个下划线。有关 Python 命名的更多信息，请查看 PEP 8 的描述性命名风格一节。

接下来，让我们看看如何实际上执行压缩。

程序清单8 trivial_compression.py 续前

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def _compress(self, gene: str) -> None:
    self.bit_string: int = 1    # start with sentinel
    for nucleotide in gene.upper():
        self.bit_string <<= 2    # shift left two bits
        if nucleotide == 'A':    # change last two bits to 00
            self.bit_string |= 0b00
        elif nucleotide == 'C':    # change last two bits to 01
            self.bit_string |= 0b01
        elif nucleotide == 'G':    # change last two bits to 10
            self.bit_string |= 0b10
        elif nucleotide == 'T':    # change last two bits to 11
            self.bit_string |= 0b11
        else:
            raise ValueError(f"Invalid Nucleotide: {nucleotide}")

_compress()方法依次查看核苷酸串中的每个字符。当它看到一个A时，它会将00添加到比特字符串中。当它看到一个C时，它会加上01，依此类推。请记住，每个核苷酸需要占两比特。因此，在添加每个新核苷酸之前，我们将位串向左移动两位（self.bit_string <<= 2）。

使用“或”操作（|）添加每个核苷酸。左移后，比特字符串右侧增加两个0。在按位运算中，0与任何值相“或”该值都会替换0。换句话说，我们不断在比特字符串的右侧添加两个新位。添加的两位由核苷酸的类型决定。

最后，我们将实现解压和特殊方法 __str__()。

程序清单9 trivial_compression.py 续前

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def decompress(self) -> str:
    gene: str = ""
    for i in range(0, self.bit_string.bit_length() - 1, 2):    # -1 to exclude sentinel
        bits: int = self.bit_string >> i & 0b11    # get just 2 relevant bits
        if bits == 0b00:    # A
            gene += "A"
        elif bits == 0b01:    # C
            gene += "C"
        elif bits == 0b10:    # G
            gene += "G"
        elif bits == 0b11:    # T
            gene += "T"
        else:
            raise ValueError(f'Invalid bits: {bits}')

    return gene[::-1]    # [::-1] reverses string by slicing backward

def __str__(self) -> str:
    return self.decompress()

decompress()一次从比特字符串中读取两位，并使用这两位来确定将哪个字符添加到基因字符串末尾。因为这些位被从后向前读取，与它们被压缩的顺序正好相反，因此需要反转（使用切片 [::-1]）。最后，请注意int中便捷的 bit_length() 方法是如何帮助开发 decompress() 的。让我们测试一下。

程序清单10 trivial_compression.py 续前

1
2
3
4
5
6
7
8
9
10
if __name__ == '__main__':
    from sys import getsizeof
    original: str = ("TACGCGTAGCCTTAAGCTACGTAAACGTCGTACGT"
                     "TCAAATTCAGGCTTTCCAATCGAACGTATGCATGCATGTCATGCCTA") * 100
    print(f"original is {getsizeof(original)} btyes")
    compressed: CompressedGene = CompressedGene(original)   # compress
    print(f"compressed is {getsizeof(compressed.bit_string)} bytes")
    print(compressed)    # decompress
    print("original and decompressed are the same: "
          "{}".format(original == compressed.decompress()))

使用 sys.getsizeof() 方法，我们可以确定是否节省了几乎75%的内存成本。

注意在 CompressedGene 类中，我们广泛使用 if 语句来决定压缩和解压方法中的各种情况。因为 Python 没有 switch 语句。有时也会在 Python 中看到对字典的高度依赖，而不是大量 if 语句来处理各种不同条件。例如，我们可以在字典中查找每个核苷酸各自的比特字符。这有时可能更易读，但可能会带来性能成本。尽管字典查找在技术上是 0(1)，但运行 hash 函数的成本有时意味着字典的性能不如一组 if。当然，这是否成立将取决于特定程序的 if 语句，必须评估什么才能得出结论。如果需要在代码的关键部分在 if 和字典查找之间做出决定，可能需要对这两种方法运行性能测试。

牢不可破的加密

一次一密（one-time pad）是一种数据加密方法，通过将数据与无意义的随机伪数据组合来加密信息，使得在不访问产品（product）和伪数据的情况下无法重构原始数据。实质上，这给加密器留下一个密钥对。一个密钥是产品，另一个是随机虚拟数据。一个密钥本身是无用的，只有两个密钥的组合才能解锁原始数据。当正确执行时，一次一密是一种不可破解的加密形式。下图显示了该过程。

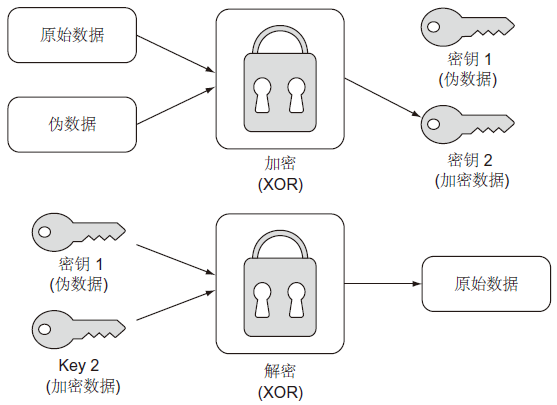
在此示例中，我们将使用一次一密加密str。Python3 的 str 可以考虑当作是 UTF-8 字节序列（bytes 类型）。str 可以通过 encode() 方法转换为 UTF-8 字节序列。同时，bytes 类型的 UTF-8 字节序列可以通过 decode() 转换会 str。

一次一密加密操作中使用的伪数据必须满足三个标准，才能使最终产品牢不可破。虚拟数据必须与原始数据长度相同，真正随机，完全保密。第一和第三个标准是常识。如果伪数据因为太短而重复，可能会出现观察到的模式。如果其中一个密钥不是真正的保密（也许它在其他地方被重复使用或者部分泄露），那么攻击者就有了线索。第二个标准本身就提出了一个问题：我们能产生真正随机的数据吗？对于大多数电脑来说答案是否定的。

在这个例子中，我们将使用来自 secrets 模块（Python3.6 中引入）的伪随机数据生成函数 token_bytes()。我们的数据不会是真正随机的，在某种意义上，secrets 包仍然在使用伪随机数生成器，但是它对于我们的目的来说已经足够了。让我们生成一个随机密钥用作伪数据。

程序清单11 unbreakable_encryption.py

1
2
3
4
5
6
7
8
9
10
from secrets import token_bytes
from typing import Tuple


def random_key(length: int) -> int:
    # generate length random bytes
    tb: bytes = token_bytes(length)
    # convert those bytes into a bit string and return it
    return int.from_bytes(tb, "big")

这个函数创建一个 int，其填充了长度为 length 的随机字节。方法 int.from_bytes() 用于从 bytes 转换为 int。与多个独立的字节组成的序列相比，按位运算（bitwise）在单个 int 上能更容易且更高效地执行。我们接下来将使用按位异或（XOR）运算。

加密与解密

那么伪数据是如何与原始数据相结合的呢？通过异或运算达到这一目的。异或是一种逻辑位运算，当其中一个操作数为真时返回 true，但当两个操作数都为真或都不为真时返回 fasle。正如你可能已经猜到的，XOR代表 “exclusive or”（异或）。

在 Python 中，XOR 运算符是 ^。在二进制位运算的上下文中，0 ^ 1 与 1 ^ 0 返回 1，而 0 ^ 0 与 1 ^ 1 返回 0。如果两个数字的位使用异或运算进行组合，一个有用的特性是得到结果可以与任一个操作数重新组合以产生另一个操作数：

1
2
3
A ^ B = C
C ^ B = A
C ^ A = B

这一关键思想构成了一次一密加密的基础。为了形成我们的加密数据，我们将简单地用原始数据 的int表示与相同长度的随机生成的int相异或。返回的密钥对（key pair）将是伪数据和加密数据。

程序清单12 unbreakable_encryption.py continued

1
2
3
4
5
6
def encrypt(original: str) -> Tuple[int, int]:
    original_bytes: bytes = original.encode()
    dummy: int = random_key(len((original_bytes)))
    original_key: int = int.from_bytes(original_bytes, "big")
    encrypted: int = original_key ^ dummy  # XOR
    return dummy, encrypted

注意：int.from_bytes()具有两个参数，第一个是我们想要转换的字节，第二个是字节序（大端）。字节序指的是用于存储数据的字节顺序。最高有效字节在前，还是最低有效字节在前？在本例中，只要在加密和解密时使用相同的顺序，那么字节序并不重要，因为我们实际上是在单个位上操纵数据。当你没有控制编码过程的两端时，字节顺序可能会出错，所以要小心！

解密是简单地重新组合encrypt()生成的密钥对的问题，通过逐位执行异或运算来实现。最终的输出必须转换回字符串。首先，使用 int.to_bytes()将 int 转换为 bytes。此方法需要提供返回字节的数量，因此需要将位的长度除以8（一个字节中的位数）。最后，bytes 方法 decode() 返回 str。

程序清单13 unbreakable_encryption.py continued

1
2
3
4
def decrypt(key1: int, key2: int) -> str:
    decrypted: int = key1 ^ key2  # XOR
    temp: bytes = decrypted.to_bytes((decrypted.bit_length() + 7) // 8, "big")
    return temp.decode()

在使用整数除法（//）除以8之前，有必要将解密数据的长度增加7，以确保我们“舍入”，从而避免 off-by-one 错误。如果我们的一次一密加密有效，我们应该能够毫无问题地加密和解密同一个 Unicode 字符串。

程序清单14 unbreakable_encryption.py continued

1
2
3
4
if __name__ == '__main__':
    key1, key2 = encrypt("One Time Pad!")
    result: str = decrypt(key1, key2)
    print(result)

如果终端输出为 “One Time Pad!”，则万事大吉。

计算 pi

数学上有意义的数字 pi（ π 或 3.14159…）可以使用许多公式导出。 其中最简单的是莱布尼兹公式。它假定以下无穷级数的收敛等于 pi：

$$\pi = \frac 41 - \frac 43 + \frac 45 - \frac 47 + \frac 49 - \frac{4}{11} \cdots$$

你会注意到无穷级数的分子为4，而分母每次递增2，对这些项的运算在加、减之间交替。

我们可以通过将公式的片段转化为函数中的变量，以一种简单的方式对该数列进行建模。分子是常数4，分母是从1开始并递增2的变量，运算可以表示为-1或1。最后，使用变量 pi 表示数列之和（通过for循环）。

程序清单15 calculating_pi.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def calculate_pi(n_terms: int) -> float:
    numerator: float = 4.0
    denominator: float = 1.0
    operation: float = 1.0
    pi: float = 0.0
    for _ in range(n_terms):
        pi += operation * (numerator / denominator)
        denominator += 2.0
        operation *= -1.0

    return pi


if __name__ == '__main__':
    print(calculate_pi(1000000))

提示 在大多数平台，Python float 类型是64位浮点数（或 C 语言中的 double 类型）。

这个函数是一个例子，说明公式和程序代码之间的机械转换在建模或模拟一个有趣的概念时是如何既简单又有效。机械转换是一个有用的工具，但我们必须记住，它不一定是最有效的解决方案。当然，pi 的莱布尼茨公式可以用更有效或更紧凑的代码来实现。

注意 无穷级数中项数越多（调用 calculate_pi() 时 n_terms 的值越大），pi 的最终计算就越准确。

汉诺塔问题

有三根垂直杆（以下简称“塔”），我们将把它们标为A、B、C。塔A上穿有圆环状圆盘。其中，最宽的圆盘在底部，我们称之为圆盘1。盘1上方的其余盘的标签数字递增，盘的直径逐渐变窄。我们的目标是在给定以下约束条件的情况下，将所有光盘从塔A移动到塔C：

  • 一次只能移动一个圆盘；
  • 每个塔仅有最上面的圆盘可以移动；
  • 宽的圆盘不能放在窄的圆盘之上。

下图描述了此问题。

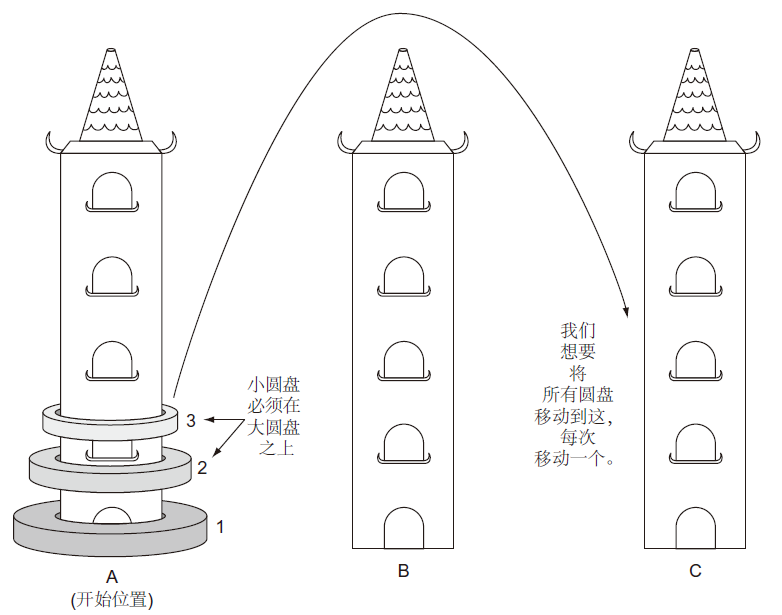
问题建模

堆栈是以后进先出（Last-In-First-Out，LIFO）概念为模型的数据结构。最后进去的最先出来。堆栈上最基本的两个操作是 push 和 pop。push 将新的一项放入堆栈，而 pop 删除并返回放入的最后一项。通过列表，我们可以轻松地在 Python 中建模堆栈。

程序清单16 hanoi.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from typing import TypeVar, Generic, List
T = TypeVar('T')


class Stack(Generic[T]):

    def __init__(self) -> None:
        self._container: List[T] = []

    def push(self, item: T) -> None:
        self._container.append(item)

    def pop(self) -> T:
        return self._container.pop()

    def __repr__(self) -> str:
        return repr(self._container)

注意 Stack 类实现了 __repr__() 以便我们可以轻松地得到塔的内容。__repr__() 是将 print() 应用于 Stack 时将输出的内容。

注意 我们将始终使用类型提示。从 typing 模块导入 Generic 使 Stack 能够在类型提示中对于特定类型是通用的。任意类型的 T 在T = TypeVar('T') 中定义。T 可以是任何类型。当类型提示用于 Stack 来解决汉诺塔问题时，它被类型提示为类型 Stack[int]，这意味着用类型 int 填充T。换句话说，堆栈是整型的堆栈。

堆栈是汉诺塔问题“塔”的完美替换。当将圆盘放入塔上时，相对于对堆栈应用 push；当将圆盘从一个塔移动到另一个塔时，相对于对一个堆栈应用pop对另个堆栈应用push。

让我们将塔定义为Stack ，并在第一个塔中放入圆盘。

程序清单17 hanoi.py continued

1
2
3
4
5
6
7
if __name__ == '__main__':
    num_discs: int = 3
    tower_a: Stack[int] = Stack()
    tower_b: Stack[int] = Stack()
    tower_c: Stack[int] = Stack()
    for i in range(1, num_discs + 1):
        tower_a.push(i)

求解汉诺塔问题

那么，如何解决汉诺塔问题？如果我们只移动一张圆盘，我们知道怎么做，是吧？事实上，移动一张圆盘是我们递归求解汉诺塔问题的基础情况（base case）。递归情况（recursive case）是移动多个圆盘。因此，关键是我们需要编写两种情况：移动一个圆盘（基础情况）和移动多个圆盘（递归情况）。

让我们看一个具体的例子来理解递归情况。假设我们有三张圆盘（顶部圆盘、中部圆盘以及底部圆盘）放在塔A上，我们想把它们移到塔C上。首先可以将顶部圆盘移动到塔C，然后可以将中间圆盘移动到塔B，再然后可以将顶部圆盘从塔C移动到塔B。现在底部圆盘仍然在塔A上，顶部圆盘在塔B上。实际上，我们现在已经成功地将两个圆盘从一个塔（A）移动到另一个塔（B）。将底部圆盘从A移动到C是我们的基本情况（移动单个圆盘）。现在，我们可以按照从A到B的相同过程将两个上盘从B移动到C。我们将顶部圆盘移动到A，中部圆盘移动到C，最后将顶部圆盘从A移动到C。

我们可以将递归情况分为三个步骤：

  1. 将前 n - 1 个圆盘从塔A移到塔B（临时塔），将C作为中继；
  2. 将最下面的圆盘从A移到C；
  3. 将 n - 1 个圆盘从B移到C，将A作为中继。

令人惊奇的是，这种递归算法不仅适用于三张圆盘，也适用于任意数量的圆盘。我们将把它编写成一个称为 hanoi() 的函数，它负责将圆盘从一个塔移动到另一个塔，并给定一个临时塔。

程序清单18 hanoi.py continued

1
2
3
4
5
6
7
def hanoi(begin: Stack[int], end: Stack[int],temp: Stack[int], n: int) -> None:
    if n == 1:
        end.push(begin.pop())
    else:
        hanoi(begin, temp, end, n - 1)
        hanoi(begin, end, temp, 1)
        hanoi(temp, end, begin, n - 1)

在调用 hanoi() 之后，你应该检查塔A、B和C，验证圆盘是否成功移动。

程序清单19 hanoi.py continued

1
2
3
4
5
6
if __name__ == '__main__':
	[... ...]
    hanoi(tower_a, tower_c, tower_b, num_discs)
    print(tower_a)
    print(tower_b)
    print(tower_c)

你会发现确实成功移动了。在编写汉诺塔问题的解决方案时，我们不一定需要了解将多个圆盘从A塔移动到C塔的每一步。但我们理解移动任意数量圆盘的通用递归算法，并编写出它，让计算机完成剩下的工作。这就是为问题制定递归解决方案的能力：我们经常能够以抽象的方式思考解决方案，而不需要陷入繁琐的细节。

顺便提一下，hanoi() 函数将根据圆盘数量执行指数部次数的调用，这使得即使仅有 64 个圆盘，算法也难以求解。可以通过更改 num_disc 变量来尝试使用其他数量的圆盘。随着圆盘数量的增加，所需步数呈指数级增长，这就是汉诺塔问题的传说来源。