细菌觅食优化算法:理论基础
Abstract. 细菌觅食优化算法(Bacterial foraging optimization algorithm,BFOA)是当前分布式优化和控制领域备受关注的全局优化算法。其受启发于大肠杆菌( Escherichia coli)的社会性觅食行为。其在解决一些应用领域中的实际优化问题的高效性引起了研究人员的关注。大肠杆菌觅食策略背后潜在的生物模式被模仿,并得到一个简单优化算法。本章从经典 BFOA 清晰的轮廓开始。然后用一个简单的数学模型来分析 BFOA 模拟趋化性步骤的动态过程。从分析的角度,提出了一种新的 BFOA 适应性变体,根据当前虚拟细菌的适应性调整趋化步长。本文还对 BFOA 繁殖算子的动态进行了分析。本章讨论了 BFOA 与其他优化技术的混合,并提供了 BFOA 到目前为止的重要应用的说明。
Introduction
由 Passino 提出的细菌觅食优化算法(Bacteria Foraging Optimization Algorithm,BFOA)[1] 是自然启发(nature-inspired)优化算法家族的新成员。在过去五十年中,遗传算法(Genetic Algorithms ,GAs)[2],进化规划(Evolutionary Programming,EP)[3],进化策略(Evolutionary
Strategies,ES)[4] 等优化算法从进化和自然遗传学中获得了灵感,占据了优化算法的半壁江山。最近自然群体启发算法,如粒子群优化(Particle Swarm Optimization,PSO)[5],蚁群优化(Ant Colony Optimization ,ACO)[6] 也凭着各自优势进入了这个领域,并证明了自身的有效性。在群(swarm-based)算法的趋势下,Passino 在文献 [1] 中提出了 BFOA。其关键思想是应用大肠杆菌群体觅食策略进行多最优函数优化( multi-optimal function optimization)。最大化每单位时间获得的能量,是细菌搜寻营养的策略。细菌个体也通过发送信号与他菌沟通。在考虑了前面的两个因素后,细菌再做觅食决定。细菌通过小步长移动寻找营养物的过程被称为趋化性,BFOA 的关键思想是模仿虚拟细菌在问题的搜索空间的趋化运动。
BFOA 自开发以来,凭借其生物学动机(biological motivation)和优美的结构,引起了不同领域的研究者的关注。研究人员正试图将 BFOA 与其他不同的算法进行混合,以便分别探索其局部和全局搜索特性。它已被应用于许多实际的问题,并证明了其在 GA 和 PSO 的许多变体中的有效性。算法的数学建模、适配和修改可能是未来 BFOA 研究的重要组成部分。
The Bacteria Foraging Optimization Algorithm
实际中细菌觅食运动是通过一组拉伸鞭毛来实现的。 翻滚和游动,这两个大肠杆菌觅食时的基本行为都是在细菌鞭毛帮助下完成的 [7,8]。 当它们沿顺时针方向旋转鞭毛时,鞭毛拉动细胞,导致每个鞭毛独立运动,最终以较小的代价翻滚,而在有害地方,为找到营养梯度则经常翻滚。 逆时针方向旋转鞭毛则有助于细菌以非常快的速度游动。 在上述算法中,细菌具有趋化性,它们喜欢朝着营养梯度移动并且避开有害的环境。 通常细菌在友好的环境中移动更长的距离。 图 1 描绘了细菌如何在营养液中发生顺时针和逆时针运动。
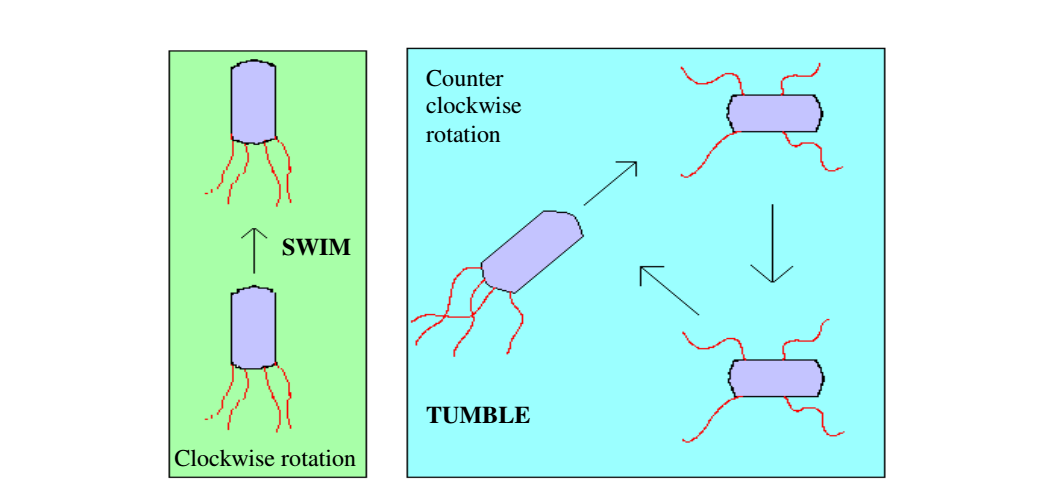
Swim and tumble of a bacterium
当他们获得充足的食物时,它们的长度会增加,并且在适当温度的情况下,它们会在中间断开而形成一个完全相同的复制品。这一现象启发了 Passino 在 BFOA 中引入了繁殖事件。由于突然的环境变化或攻击的发生,趋化过程可能被破坏,细菌群可能会移动到其他地方,或者其他地方的细菌可能被引入到当前群体中。这构成了现实中细菌群的 elimination-dispersal 事件,即,一个地区的所有细菌都被杀死,或细菌群移动到新环境中。
现在假设我们想要最小化 $J(\theta)$,其中 $\theta \in \Re^p$ (例如,$\theta$ 是 p 维实数向量),而梯度 $\nabla J(\theta)$ 没有测量或分析解。 BFOA 模拟了真实细菌系统中观察到的四种主要机制:趋化、群集、繁殖和 elimination-dispersal,以解决该非梯度优化问题。虚拟细菌实际上是在函数表面移动以期获得全局最优的一个试解(可以称之为搜索代理(search-agent))。
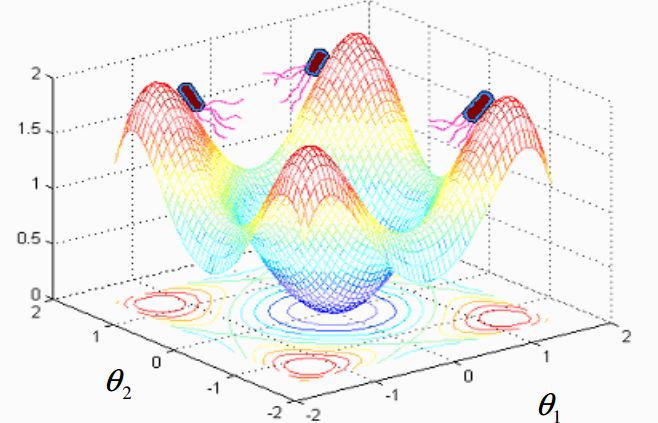
A bacterial swarm on a multi-modal objective function surface.
定义一个趋化性过程为,翻转后接着翻转,或翻转后接着游动。令 $j$ 为趋化性过程的索引(index)。令 $k$ 为繁殖过程的索引。令 $l$ 为 elimination-dispersal 事件的索引。还令
  $p$:搜索空间维度
  $S$:种群中细菌总数
  $N_C$:趋化性过程的总数
  $N_s$:游动长度
  $N_{re}$:繁殖过程的总数
  $N_{ed}$:elimination-dispersal 事件的总数
  $P_{ed}$:elimination-dispersal 事件发生的概率
  $C(i)$:翻转到随机方向所需步骤
$P(j,k,l)={ \theta^i(j,k,l)|i=1,2,…,S }$ 表示种群中细菌 i,第 j 个趋化性过程,第 k 个繁殖过程,第 l 个 elimination-dispersal 事件。令 $J(i,j,k,l)$ 表示第 i 个细菌在位置 $\theta^i (j,k,l) \in \Re^p$(有时候我们直接写成 $\theta^i$ )的代价。需要注意的是,对 J 的称谓可以是代价(优化理论术语)也可以是营养表面(生物学)。对于实际的细菌种群,S 可能非常大(例如,$S=109$),但 $p=3$。在计算机模拟中,使用的种群尺寸会小一些,且其值是固定的。而且,在 BFOA 中下,允许 $p>3$ 如此我们就能将该方法用于高维优化问题。下面我们简要地描述一下 BFOA 的四个首要步骤
  i) 趋化性: 模拟了大肠杆菌通过鞭毛游动和翻转的运动过程。从生物学上讲,大肠杆菌可以以两种不同的方式移动。它可以在同一方向游动一段时间也可以翻转,并且在整个生命周期内交替使用这两种模式。细菌的趋化性运动可以表示为
$$\theta^i(j+1,k,l) = \theta^i(j,k,l)+C(i) \frac{\Delta (i)}{\sqrt{\Delta^T(i)\Delta(i)}}, \tag 1$$
其中 $\Delta$ 表示随机方向上取值为 [-1, 1] 的向量。
  ii) 游动: 观察到一些有趣的细菌群体行为(包括大肠杆菌和鼠伤寒沙门氏菌)—— 细菌在半固体营养培养基中形成复杂而稳定的时空模式(群)。当向半固体基质中加入单个营养化学效应物(chemo-effecter)时,细菌群会排列成一个环,通过环移动爬上营养梯度。细胞受到高水平琥珀酸(succinate)刺激,释放能够使它们聚集成群的引诱剂(aspertate),从而以高细菌密度的群集形式移动。大肠杆菌群中的细胞到细胞的信号传递可以由以下函数表示
$$
\begin{align}
J_{cc}(\theta,P(j,k,l)) & = \sum_{i=1}^S J_{cc}(\theta, \theta^i(j,k,l)) \
& = \sum_{i=1}^S[-d_{attractant}exp(-w_{attractant} \sum_{m=1}^p(\theta_m - \theta_m^i)^2)]+\sum_{i=1}^S[h_{repellant}exp(-w_{repellant}\sum_{m=1}^p(\theta_m-\theta_m^i)^2)]
\end{align} \tag 2
$$
其中 $J_{cc}(\theta,P(j,k,l))$ 是要加入到实际目标函数的目标函数值,用于呈现目标函数的时变性。$\theta = [\theta_1 \theta_2 ,..., \theta_p]^T$ 是 p 维搜索域中的一点。$d_{attractant}, w_{attractant}, h_{repellant}, w_{repellant}$ 是不同的系数 [1, 9]。
  iii) 繁殖: 不健康的细菌最终会死亡,而健康的细菌(产生较低目标函数值的细菌)分裂成两个细菌,然后放置在相同位置。以使群体大小保持不变。
  iv) Elimination-Dispersal: 由于各种原因,可能会出现细菌种群居住的局部环境发生渐变或突变。例如,温度的显著升高可能会杀死目前处于高浓度营养梯度位置的细菌群。下面这些事件可能会发生,即一个地区的所有细菌都被杀死,或一群细菌扩散到一个新的区域。为了在 BFOA 中模拟这种现象,细菌会被以非常小的概率清除,而新的细菌在搜索空间被随机地初始化。
下面是算法的伪代码:
The BFOA Algorithm
Parameters:
[Step 1] Initialize parameters $p,S,N_C,N_S,N_{re},N_{ed},P_{ed},C(i)(i=1,2,...,S),\theta^i$
Algorithm:
[Step 2] Elimination-dispersal loop: $l=l+1$
[Step 3] Reproduction loop: $k=k+1$
[Step 4] Chemotaxis loop: $j=j+1$
  [a] For $i =1,2,...,S$ take a chemotactic step for bacterium i as follows.
  [b] Compute fitness function, $J(i, j, k, l)$. Let, $J(i,j,k,l) = J(i,j,k,l) +J_{cc}(\theta^i(j,k,l), P(j,k,l))$ (i.e. add on the cell-to cell attractant–repellant profile to simulate the swarming behavior) where, $J_{cc}$ is defined in (2).
  [c] Let $J_{last} = J(i,j,k,l)$ to save this value since we may find a better cost via a run.
  [d] Tumble: generate a random vector $\Delta \in \Re^p$ with each element $\Delta_m(i), m=1,2,...,p$, a random number on [-1, 1].
  [e] Move: Let $\theta^i(j+1,k,l) = \theta^i(j,k,l)+C(i) \frac{\Delta(i)}{\sqrt{\Delta^T(i) \Delta(i)}}$ This results in a step of size C(i) in the direction of the tumble for bacterium i.
  [f] Compute $J(i,j+1,k,l)$ and let $J(i,j+1,k,l)=J(i,j,k,l)+J_{cc}(\theta^i(j+1,k,l),P(j+1,k,l))$
  [g] Swim
   i) Let $m=0$ (counter for swim length).
   ii) While $m < N_S$ (if have not climbed down too long).
   Let $m=m+1$.
   If $J(i,j+1,k,l) < J_{last}$ (if doing better), let $J_{last}=J(i,j+1,k,l)$ and let $\theta^i(j+1,k,l) = \theta^i(j,k,l)+C(i)\frac{\Delta(i)}{\sqrt{\Delta^T(i)\Delta{i}}}$. And us this $\theta^i(j+1,j,k)$ to compute the new $J(i,j+1,k,l)$ as we did in [f]
   Else, let $m = N_S$. This is the end of the while statement.
  [h] Go to next bacterium $(i+1)$ if $i \ne S$ (i.e., go to [b] to process the next bacterium).
[Step 5] If $j < N_C$, go to step 4. In this case continue chemotaxis since the life of the bacteria is not over.
[Step 6] Reproduction:
   [a] For the given k and l, and for each $i=1,2,...,S$, let $J_{health}^i=\sum_{j=1}^{N_C+1}J(i,j,k,l)$ be the health of the bacterium i (a measure of how many nutrients it got over its lifetime and how successful it was at avoiding noxious substances). Sort bacteria and chemotactic parameters $C(i)$ in order of ascending cost $J_{health}$ (higher cost means lower health).
   [b] The $S_r$ bacteria with the highest $J_{health}$ values die and the remaining $S_r$ bacteria with the best values split (this process is performed by the copies that are made are placed at the same location as their parent).
[Step 7] If $k < N_{re}$ , go to step 3. In this case, we have not reached the number of specified reproduction steps, so we start the next generation of the chemotactic loop.
[Step 8] Elimination-dispersal: For $i=1,2,...,S$ with probability $P_{ed}$ , eliminate and disperse each bacterium (this keeps the number of bacteria in the population constant). To do this, if a bacterium is eliminated, simply disperse another one to a random location on the optimization domain. If $l < N_{ed}$ , then go to step 2; otherwise end.
本文翻译自 Das S, Biswas A, Dasgupta S, et al. Bacterial foraging optimization algorithm: theoretical foundations, analysis, and applications[J]. Foundations of Computational Intelligence Volume 3, 2009: 23-55. 有删节