曲率与自动微分

发表于 更新于 分类于 阅读次数：

手动计算曲率十分枯燥，因为它涉及计算一阶导与二阶导。当然，也有其他的应用需要求导，但在这里我们将曲率作为例子。

求导

如果只用显式地实现原始函数，然后让软件自己找出导数，就好了。

数值微分

导数的有限差分近似并不新鲜。例如，欧拉（1707-1783）使用有限差分（数值）求解微分方程。但数值微分可能不准确或不稳定，特别是对于高阶导数。

符号微分

符号微分是另一种方法，让计算机像人们手动一样操纵表达式。它适用于很多问题，但对于大问题来说，可扩展性不行。它还要求函数以传统的数学形式呈现，而不是以源代码的形式呈现。

自动微分

自动微分是第三种方法。像数值微分一样，它可以与浮点数一起使用，而不是符号表达式。但与数值微分不同，结果没有近似误差。正如有人所说，自动微分将链式规则应用于浮点数而不是符号表达式。

Python 实现

我将使用 Python 库 autograd 来计算曲率并说明自动微分。autograd并不是 Python 最强大的自动微分库，但它是我见过的最简单的。

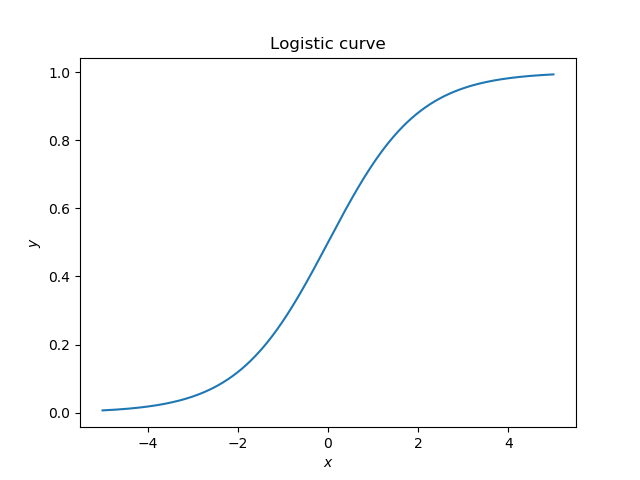
我们将计算逻辑曲线的曲率。

$$y=\frac{1}{1+e^{-x}}$$

曲率由下式给出：

$$\kappa (x)=\frac{|y^{‘’}|}{(1+y^{‘2})^{3/2}}$$

下面是使用 autograd 计算曲率的 Python 代码。

1
2
3
4
5
6
7
8
9
10
11
import autograd.numpy as np
from autograd import grad

def f(x):
    return 1/(1 + np.exp(-x))

f1 = grad(f)  # 1st derivative of f
f2 = grad(f1) # 2nd derivative of f

def curvature(x):
    return abs(f2(x))*(1 + f1(x)**2)**-1.5

绘图

该图在中间和远端相对平坦。而在此之间，形成了两个曲率较高的区域。

1
2
3
4
5
6
7
8
import matplotlib.pyplot as plt

x = np.linspace(-5, 5, 300)
plt.plot(x, f(x))
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.title("Logisitic curve")
plt.savefig("logistic_curve.svg")

看一下曲率：

1
2
3
4
5
6
y = [curvature(t) for t in x]
plt.plot(x, y)
plt.xlabel("$x$")
plt.ylabel(r"$\kappa(x)$")
plt.title("Curvature")
plt.savefig("plot_logistic_curvature.svg")

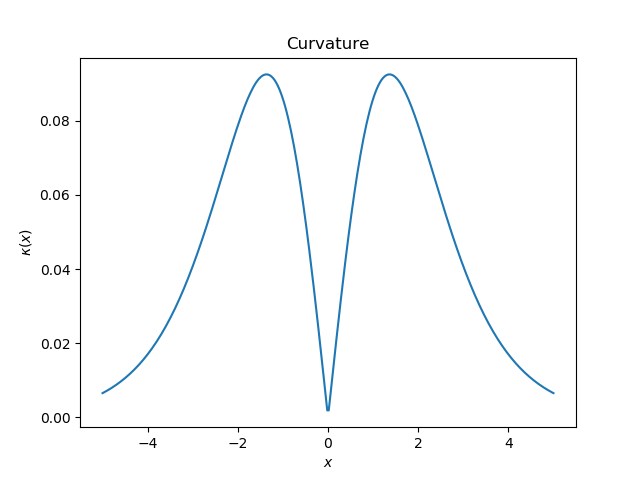
正如我们应该预料的那样，曲率在远端和中间是很小的，其间具有局部最大值。

我们还可以查看符号（signed）曲率，与曲率相同的表达式，但没有绝对值。

$$k(x) = \frac{y^{‘’}}{(1+y^{‘2})^{3/2}}$$

使用以下代码绘图：

1
2
3
4
5
6
7
8
9
def signed_curvature(x):
    return f2(x)*(1 + f1(x)**2)**-1.5

y = [signed_curvature(t) for t in x]
plt.plot(x, y)
plt.xlabel("$x$")
plt.ylabel(r"$k(x)$")
plt.title("Signed curvature")
plt.savefig("graph_signed_curvature.svg")

结果看起来像正弦曲线。

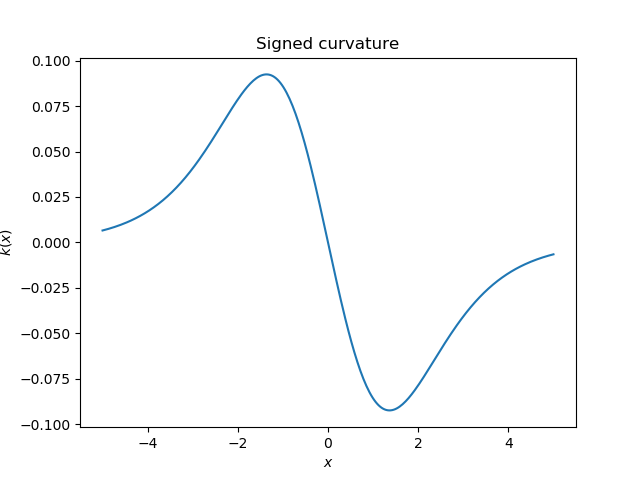
正值表示曲线逆时针弯曲，负值表示曲线顺时针弯曲。

本文翻译自：Curvature and automatic differentiation