数值 Python: 符号计算

发表于 2018-04-01 更新于 2022-11-09 阅读次数：

与基于数值数组的计算相比，符号计算是一种完全不同的计算模式。符号计算也被称为计算机代数系统（computer algebra systems，CAS），数学对象和表达式的表示被分析地操纵和转换。符号计算主要是将原则上需要使用笔和纸手动完成的计算，使用计算机自动进行分析计算。

分析和符号计算是科技计算领域的一个关键部分，即使对于只能用数值方法解决的问题（分析方法在许多实际问题中是不可行），在采用数值方法之前，它也能分析性的推动限制，从而产生很大不同。例如，可以减少最终需要解决的数值问题的复杂性或大小。换句话说，在使用数值方法之前先使用分析方法简化问题。

在科学 Python 环境中，符号计算的主要库是 SymPy（Symbolic Python）。 SymPy 完全用 Python 编写，为各种分析和符号问题提供了工具。

导入 SymPy

1
2
3

In [1]: import sympy

In [2]: sympy.init_printing()

这里我们还调用了 sympy.init_printing 函数，它用于配置 SymPy 打印系统以显示良好格式化的数学表达式。在 IPython 中，它会使用 MathJax JavaScript 库来渲染 SymPy 表达式。

为了寻求方便和可读性，我们也假设以下常用符号是显式地从 SymPy 中导入到本地命名空间的。

1	In [3]: from sympy import I, pi, oo

符号

SymPy 的核心功能是将数学符号表示为 Python 对象。在 SymPy 库中，类 sympy.Symbol 可用于此目的。Symbol 的一个实例有一个名称和一组描述其特性的属性，以及用于查询这些特性和用于操纵符号对象的方法。一个符号本身并没有多少实际用途，但它们被当作表达式树中的节点，来表示代数表达式。

符号名是一个字符串，可以选择性地包含类 LaTeX 的标记，以使符号名在富显示系统（如， IPython）良好地展示。Symbol 对象的名称在创建时会被给定。在 SymPy 中有以下几种不同的方式创建符号，使用 sympy.Symbol、sympy.symbols 和 sympy.var。通常，希望将 SymPy 符号与具有相同名称（或具有紧密联系）的 Python 变量相关联。如：

1	In [4]: x = sympy.Symbol("x")

变量 x 现在表示一个抽象的数学符号 x，默认情况下知道的信息非常少。此时，x 可以表示例如实数、整数、复数、函数以及大量其他可能。在很多情况下，用这个抽象的、未指定的 Symbol 对象表示一个数学符号就足够了，但有时需要给 SymPy 更多的信息，以确切知道 Symbol 对象代表具体什么类型的符号。这可以帮助 SymPy 更有效地操纵分析表达式。我们可以添加各种假设，以缩小符号类型潜在的可能。下表总结了可以与 Symbol 类实例关联的一些常用假设的选择。

假设的关键字参数	属性	描述
real, imaginary	is_real, is_imaginary	指定一个符号代表实数或虚数
positive, negative	is_positive, is_negative	指定一个符号代表正数或负数
integer	is_integer	该符号代表整数
odd, even	is_odd, is_even	该符号代表奇数或偶数
prime	is_prime	该符号代表质数
finite, infinite	is_finite, is_infinite	该符号代表有限或无限

In [2]: y = sympy.Symbol("y", real=True)

In [3]: y.is_real
Out[3]: True

In [4]: x = sympy.Symbol("x")

In [6]: x.is_real is None
Out[6]: True

In [7]: sympy.Symbol("z", imaginary=True).is_real
Out[7]: False

注意：如果知道符号是实数，is_real 返回 True，如果知道符号不是实数，则返回 False，如果不知道符号到底是实数还是非实数，那么返回 None。

根据上表，创建新符号时最重要的是明确符号是实数还是虚数，以及是正数还是负数。

In [8]: y = sympy.Symbol("y", positive=True)

In [9]: x = sympy.Symbol("x")

In [11]: sympy.sqrt(x ** 2)
Out[11]:
   ____
  ╱  2
╲╱  x

In [12]: sympy.sqrt(y ** 2)
Out[12]: y

当数学符号表示的是整数而不仅仅是实数时，明确指定符号类型也是有用的。例如设置 integer=True 或 even=True 或 odd=True。这可以让 SymPy 分析性地简化某些表达式和函数评估。例如：

In [13]: n1 = sympy.Symbol("n")

In [14]: n2 = sympy.Symbol("n", integer=True)

In [15]: n3 = sympy.Symbol("n", odd=True)

In [19]: sympy.cos(n1 * pi)
Out[19]: cos(πn)

In [20]: sympy.cos(n1*pi)
Out[20]: cos(πn)

In [21]: sympy.cos(n2 * pi)
Out[21]:
    n
(-1)

In [22]: sympy.cos(n3 * pi)
Out[22]: -1

对于某些需要大量符号的数学问题，使用逐个指定每个符号会变得单调乏味。这时候需要使用 sympy.symbols。

1
2
3

In [24]: a, b, c = sympy.symbols("a, b, c", negative=True)

In [25]: d, e, f = sympy.symbols("d, e, f", positive=True)

数字

将数学符号表示为 Python 对象的目的是在数学表达式的表达式树中使用它们。为了能够做到这一点，我们还需要表示其他数学对象，如数字、函数和常量。

我们不能直接使用 Python 内置的整数 int 和浮点数 float，
SymPy 提供了用于在 SymPy 框架内表示整数和浮点数的类 sympy.Integer 和 sympy.Float。在使用 SymPy 时，这一区别非常重要。但是我们很少需要考虑到这一点，这是因为当遇到 SymPy 表达式时，SymPy 自动地提升了 Python 内置类型。下例展示了两者的不同之处。

In [26]: i = sympy.Integer(19)

In [27]: type(i)
Out[27]: sympy.core.numbers.Integer

In [29]: i.is_Integer, i.is_real, i.is_odd
Out[29]: (True, True, True)

In [30]: f = sympy.Float(2.3)

In [31]: type(f)
Out[31]: sympy.core.numbers.Float

In [32]: f.is_Integer, f.is_real, f.is_odd
Out[32]: (False, True, False)

要创建一个数字的 SymPy 表示，或者说任意表达式，我们也可以使用 sympy.sympify 函数。该函数接受各种输入并派生一个SymPy兼容表达式，并且不需要明确指定要创建什么类型的对象。对于数字输入的简单情况，我们可以使用：

In [3]: i, f = sympy.sympify(19), sympy.sympify(2.3)

In [4]: type(i), type(f)
Out[4]: (sympy.core.numbers.Integer, sympy.core.numbers.Float)

整数（Integer）

在上一节中，我们使用了 Integer 类来表示整数。值得指出的是，在 Symbol 实例设置 integer = True 与直接使用 Integer 实例是存在差异。integer = True 表示某个整数，Integer 实例表示特定的整数。对于这两种情况，is_integer 属性都为 True，但属性 is_Integer，只对 Integer 实例为 True。一般情况下，名称为 is_Name 的属性指示对象是否为 Name 类型，名称为 is_name 的属性指示对象是否满足已知条件。

In [10]: n.is_integer, n.is_Integer, n.is_positive, n.is_Symbol
Out[10]: (True, False, None, True)

In [11]: i.is_integer, i.is_Integer, i.is_positive, i.is_Symbol
Out[11]: (True, True, True, False)

SymPy 中的整数是任意的精度，这意味着它们没有固定的下限和上限，因此可以使用非常大的数字，如下所示：

In [12]: i ** 50
Out[12]: 8663234049605954426644038200675212212900743262211018069459689001

In [13]: sympy.factorial(100)
Out[13]:
933262154439441526816992388562667004907159682643816214685929638952175999932299
156089414639761565182862536979208272237582511852109168640000000000000000000000
00

浮点（Float）

在前面，我们也遇到过类型 sympy.Float。与 Integer 类似，Float 也是任意精度的，这与 Python 的内置浮点类型和 NumPy 中的浮点类型不同。这意味着任何 Float 都可以表示具有任意小的浮点数。当使用其构造函数创建 Float 实例时，有两个参数：第一个参数是 Python 浮点数或表示浮点数的字符串，第二个（可选）参数是精度（有效小数位数）。众所周知，实数 0.3 不能完全表示为正常的固定位大小的浮点数，当打印20个有效数字的 0.3 时，它被替换为 0.2999999999999999888977698。SymPy Float 对象可以表示实数 0.3 而不受浮点数的限制：

In [16]: "%.25f" % 0.3
Out[16]: '0.2999999999999999888977698'

In [17]: sympy.Float(0.3, 25)
Out[17]: 0.2999999999999999888977698

In [18]: sympy.Float('0.3', 25)
Out[18]: 0.3000000000000000000000000

有理数（Rational）

有理数是两个整数 p, q，的分数 p/q。SymPy 使用类 sympy.Rational 表示这种类型的数。

In [3]: sympy.Rational(11, 13)
Out[3]:
11
──
13

In [4]: r1 = sympy.Rational(2, 3)

In [5]: r2 = sympy.Rational(4, 5)

In [6]: r1 * r2
Out[6]: 8/15

In [7]: r1 / r2
Out[7]: 5/6

常数与特殊符号

SymPy 提供了多种数学常数和特殊对象的预定义符号，如下表所示：

数学符号	SymPy 符号	描述
$\pi$	sympy.pi	圆的周长与直径之比
$e$	sympy.E	自然对数的底
$\gamma$	sympy.EulerGamma	欧拉常数
$i$	sympy.I	虚数单位
$\infty$	sympy.oo	无穷

函数

在 SymPy 中，可以使用 sympy.Function 创建表示函数的对象。SymPy 区分定义函数和未定义函数，以及应用（applied）函数和未应用函数。使用 Function 创建函数会产生未定义（抽象）、未应用函数，该函数仅仅具有一个名称，由于未定义其表达式或主体，因此无法对其进行求值。这样的函数可以表示具有任意个输入变量的任意函数。

In [3]: x, y, z = sympy.symbols("x, y, z")

In [4]: f = sympy.Function("f")

In [5]: type(f)
Out[5]: sympy.core.function.UndefinedFunction

In [6]: f(x)
Out[6]: f(x)

In [7]: g = sympy.Function("g")(x, y, z)

In [8]: g
Out[8]: g(x, y, z)

In [9]: g.free_symbols
Out[9]: set([x, y, z])

这里我们还使用了 free_symbols 属性，它返回给定表达式（在这里是函数 g）中包含的一组唯一符号，以表明应用函数确实与一组特定的输入符号相关联。当我们考虑抽象函数的导数时这会很重要。未定义函数的一个重要应用是用于微分方程（或者说，函数的关系式是已知的，但函数本身是未知的）。

与未定义函数相比，已定义函数具有特定的实现，并且可以对所有有效的输入参数进行数值计算。可以通过子类化 sympy.Function 来定义这种类型的函数，但在大多数情况下，使用 SymPy 提供的数学函数就足够了。在 SymPy 全局命名空间（请参阅 sympy.functions.elementary、sympy.functions.combinatorial 和 sympy.functions.special 模块及其子模块的文档）中有许多可用的 SymPy 内置标准数学函数。

In [10]: sympy.sin
Out[10]: sin

In [11]: sympy.sin(x)
Out[11]: sin(x)

In [13]: sympy.sin(pi * 1.5)
Out[13]: -1

当应用抽象符号（如 x）时，sin 函数保持未评估状态，但在某些情况下，会给出数值：

In [14]: n = sympy.Symbol("n", integer=True)

In [15]: sympy.sin(pi * n)
Out[15]: 0

另一类 SymPy 函数是 lambda 函数或匿名函数。可以使用 sympy.Lambda 创建匿名函数：

In [5]: h = sympy.Lambda(x, x**2)

In [6]: h
Out[6]: 
     2
x ↦ x 

In [7]: h(5)
Out[7]: 25

In [8]: h(1+x)
Out[8]: 
       2
(x + 1)

表达式

前一节介绍的各种符号是表示数学表达式所需的基本构件。在 SymPy 中，数学表达式被表示为树结构，树中叶是符号、节点是表示数学运算的类实例。这些类有用于基本算术运算的 Add、Mul 和 Pow 以及用于分析数学运算的 Sum、Product、Integral 和 Derivative。当然，还有许多其他的数学运算类。

考虑数学表达式 $1+2x^2+3x^3$ 。为了在 SymPy 中表示这一点，我们只需要创建符号 x，然后将表达式写为 Python 代码：

In [3]: x = sympy.Symbol("x")

In [4]: expr = 1 + 2 * x**2 + 3 * x**3

In [5]: expr
Out[5]:
   3      2
3⋅x  + 2⋅x  + 1

这里 expr 是 Add 的一个实例，子表达式为 1、2 * x ** 2 和 3 * x ** 3。下图显示了 expr 整个表达式树。

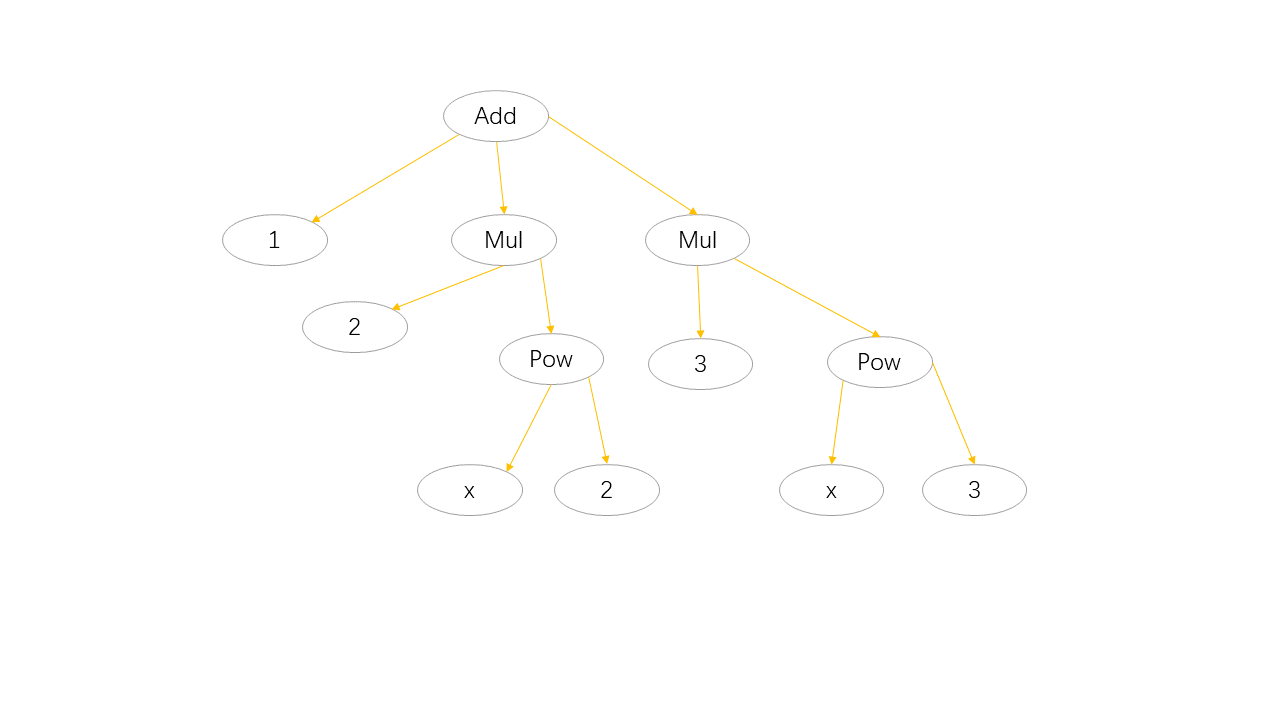
可以使用 args 属性显式遍历表达式树。

In [6]: expr.args
Out[6]:
⎛      2     3⎞
⎝1, 2⋅x , 3⋅x ⎠

In [7]: expr.args[1]
Out[7]:
   2
2⋅x

In [8]: expr.args[1].args[1]
Out[8]:
 2
x

In [9]: expr.args[1].args[1].args[0]
Out[9]: x

In [11]: expr.args[1].args[1].args[0].args
Out[11]: ()

在 SymPy 的基本使用中，很少需要显式操作表达式树，但是当操作表达式的方法不够用时，使用 args 属性实现自己的函数来遍历和操作表达式树是有用的。

操纵表达式

操作表达式树是 SymPy 的主要工作之一，SymPy 为不同类型的转换提供了许多函数。总体思路是表达式树可以（通过化简和重写）在数学等价形式之间进行转换。SymPy 中的表达式被视为不可变对象，它不会修改传递过来的函数，而是创建一个新的函数。

化简

对一个数学表达式而言，最想要的操作是化简它。这可能也是最模糊的操作，因为从算法上确定一个表达式比其他的表达式对人类而言简单，是复杂的。而且，采用哪种方法来获取更简单的表达式，通常也是不明显的。尽管如此，任何 CAS 都提供了黑盒化简功能，SymPy 提供了 sympy.simplify 函数用于化简给定表达式。化简函数也可以通过 simplify 方法调用。

In [6]: expr = 2 * (x**2 - x) - x*(x+1)

In [7]: expr
Out[7]:
   2
2⋅x  - x⋅(x + 1) - 2⋅x

In [8]: sympy.simplify(expr)
Out[8]: x⋅(x - 3)

In [9]: expr.simplify()
Out[9]: x⋅(x - 3)

In [10]: expr
Out[10]:
   2
2⋅x  - x⋅(x + 1) - 2⋅x

一般地，sympy.simplify 会尝试不同的策略，它也会化简三角函数和幂函数。

In [11]: expr = 2 * sympy.cos(x) * sympy.sin(x)

In [12]: expr
Out[12]: 2⋅sin(x)⋅cos(x)

In [13]: sympy.simplify(expr)
Out[13]: sin(2⋅x)

In [16]: expr = sympy.exp(x)*sympy.exp(y)

In [17]: expr
Out[17]:
 x  y
ℯ ⋅ℯ

In [18]: sympy.simplify(expr)
Out[18]:
 x + y
ℯ

对于三角函数和幂函数这些特定类型的化简，也可以用更具体的函数来执行，例如 sympy.trigsimp 和 sympy.powsimp。这些函数仅执行其名称所指示的化简，并将表达式的其他部分保留其原始形式。下表给出了常见的化简函数。当已知精确的简化步骤时，最好使用具体的简化函数，因为它们的操作更加明确，并且不太可能在未来版本的 SymPy 中更改。而 sympy.simplify 函数依赖于未来可能会发生变化的启发式方法，因此对于特定的输入表达式会产生不同的结果。

函数	描述
`sympy.simplify`	尝试使用各种方法获取给定表达式的更简单形式
`sympy.trigsimp`	尝试使用三角恒等式简化表达式
`sympy.powsimp`	尝试使用幂法则简化表达式
`sympy.compsimp`	简化组合表达式
`sympy.ratsimp`	通过使用公分母来简化表达

展开

函数 sympy.expand 执行各种形式的展开，具体形式取决于可选关键字参数的值。默认情况下，该函数将和的乘积完全展开。例如， $(x+1)(x+2)$ 被展开为 $x^2+3x+2$ ：

In [7]: expr = (x + 1) * (x + 2)

In [9]: sympy.expand(expr)
Out[9]:
 2
x  + 3⋅x + 2

一些可用的关键字参数包括 mul=True 展开乘积，trig=True 三角扩展。

1 2	In [12]: sympy.sin(x + y).expand(trig = True) Out[12]: sin(x)⋅cos(y) + sin(y)⋅cos(x)

log=True 对数展开，

In [14]: a, b = sympy.symbols("a, b", positive=True)

In [15]: sympy.log(a * b).expand(log=True)
Out[15]: log(a) + log(b)

complex=True 分离表达式的实部和虚部，

In [16]: sympy.exp(I*a + b).expand(complex=True)
Out[16]:
   b           b
ⅈ⋅ℯ ⋅sin(a) + ℯ ⋅cos(a)

power_base=True 和 power_exp=True 分别展开幂表达式的底和指数。

In [17]: sympy.expand((a * b)**x, power_base=True)
Out[17]:
 x  x
a ⋅b

In [18]: sympy.exp((a - b)*x).expand(power_exp=True)
Out[18]:
 a⋅x  -b⋅x
ℯ   ⋅ℯ

Factor, Collect, and Combine

sympy.factor 可以用来对代数表达式进行因式分解。在某种程度上，这是对 mul=True 的 sympy.expand 的反向操作：

In [19]: sympy.factor(x**2 - 1)
Out[19]: (x - 1)⋅(x + 1)

In [21]: sympy.factor(x * sympy.cos(y) + sympy.sin(x) * x)
Out[21]: x⋅(sin(x) + cos(y))

其他的一些相反操作有：sympy.trigsimp、sympy.powsimp 和 sympy.logcombine。

In [22]: sympy.logcombine(sympy.log(a) - sympy.log(b))
Out[22]:
   ⎛a⎞
log⎜─⎟
   ⎝b⎠

在处理数学表达式时，通常需要对因子进行细粒度的控制。SymPy 函数 sympy.collect 因式分解包含给定符号或符号列表的项。例如，x+y+xyz 不能被完全因式分解，但能够部分的分解，使之包含 x 或 y 项：

In [24]: expr = x + y + x*y*z

In [25]: expr.collect(x)
Out[25]: x⋅(y⋅z + 1) + y

In [26]: expr.collect(y)
Out[26]: x + y⋅(x⋅z + 1)

In [28]: expr = sympy.cos(x + y) + sympy.sin(x - y)

In [29]: expr.expand(trig=True).collect([sympy.cos(x), sympy.sin(x)]).collect(sympy.cos(y) - sympy.sin(y))
Out[29]: (sin(x) + cos(x))⋅(-sin(y) + cos(y))

Apart, Together, and Cancel

这里我们将要考虑的最后一种数学化简是重写分数。函数 sympy.apart 和 sympy.together 分别是将分数分解成多个部分和将多个分数组合成一个分数。

In [4]: sympy.apart(1/(x**2 + 3*x + 2), x)
Out[4]:
    1       1
- ───── + ─────
  x + 2   x + 1

In [5]: sympy.together(1/ (y*x + y)+1 / (1+x))
Out[5]:
  y + 1
─────────
y⋅(x + 1)

In [6]: sympy.cancel(y/(y*x + y))
Out[6]:
  1
─────
x + 1

替换

数学表达式操作的另一种常用形式是表达式内的符号或子表达式的替换。例如，我们可能想要进行变量替换，用 y 替换变量 x，或者用另一个表达式替换一个符号。在 SymPy 中有两种进行替换的方法：subs 和 replace。通常情况下，subs 是最合适的选择，但在某些情况下，replace 可提供更强大的工具（例如，可基于通配符）。

In [7]: (x + y).subs(x, y)
Out[7]: 2⋅y

In [9]: sympy.sin(x * sympy.exp(x)).subs(x, y)
Out[9]:
   ⎛   y⎞
sin⎝y⋅ℯ ⎠

当需要进行多次替换时，我们可以将字典作为第一个也是唯一的参数传递给 subs，这样可以将旧的符号或表达式映射到新的符号或表达式：

In [11]: sympy.sin(x * z).subs({z: sympy.exp(y), x: y, sympy.sin: sympy.cos})
Out[11]:
   ⎛   y⎞
cos⎝y⋅ℯ ⎠

subs 方法的一个典型应用是用数字代替符号来进行数值计算。一种简单方法是定义一个字典，将符号转换为数字，并将该字典作为参数传递给 subs 方法。

In [12]: expr = x * y + z  **2 *x

In [13]: values = {x: 1.25, y: 0.4, z: 3.2}

In [14]: expr.subs(values)
Out[14]: 13.3000000000000

数值计算

可以使用 sympy.N 函数或 SymPy 表达式实例的 evalf 方法来计算 SymPy 表达式：

In [5]: sympy.N(1+pi)
Out[5]: 4.14159265358979

In [6]: sympy.N(pi, 50)
Out[6]: 3.1415926535897932384626433832795028841971693993751

In [7]: (x + 1/pi).evalf(10)
Out[7]: x + 0.3183098862

sympy.N 和 evalf 方法都带有一个可选参数，该参数指定要计算表达式的有效位数。如上所示，SymPy 的多精度浮点数能够用来计算高达 50 位的 $\pi$ 值。

当我们需要对一系列输入值进行数值计算时，原则上我们可以通过对这些数进行循环，然后逐个执行 evalf 调用，例如：

In [8]: expr = sympy.sin(pi * x* sympy.exp(x))

In [9]: [expr.subs(x, xx).evalf(3) for xx in range(0, 10)]
Out[9]: [0, 0.774, 0.642, 0.722, 0.944, 0.205, 0.974, 0.977, -0.87, -0.695]

但是，此方法相当低效，SymPy 使用函数 sympy.lambdify 为执行这类操作提供了更高效的方法。该函数将一组自由符号和一个表达式作为参数，并生成一个可高效评估表达式数值的函数。生成函数的参数数量与传递给 sympy.lambdify 第一个参数的自由符号的数量相同。

In [10]: expr_func = sympy.lambdify(x, expr)

In [11]: expr_func(1.0)
Out[11]: 0.773942685266709

请注意，函数 expr_func 需要数字（标量）值作为参数，所以我们不能将符号作为参数传递给此函数，这是严格的数值计算。前面的例子所中创建的 expr_func 是一个标量函数，与 NumPy 数组形式的矢量化输入不直接兼容。SymPy 也能够生成 NumPy 数组兼容的函数——通过将可选参数 numpy 作为第三个参数传递给 sympy.lambdify 就可创建一个接受 NumPy 数组作为输入的矢量化函数。这通常是计算具有大量输入参数的符号表达式的最有效的方法。

In [12]: expr_func = sympy.lambdify(x, expr, 'numpy')

In [13]: import numpy as np

In [14]: xvalues = np.arange(0, 10)

In [15]: expr_func(xvalues)
Out[15]:
array([ 0.        ,  0.77394269,  0.64198244,  0.72163867,  0.94361635,
        0.20523391,  0.97398794,  0.97734066, -0.87034418, -0.69512687])

这通常是从 SymPy 表达式中生成数据的有效方式。例如，用于绘图和其他面向数据应用。

数学计算

到目前为止，我们已经看过如何在 SymPy 中表示数学表达式，以及如何对这些表达式进行基本的简化和转换。有了这个框架，我们就可以准备探索符号微积分（符号分析），这是应用数学的基石，在整个科学和工程领域有大量的应用。微积分的核心概念是随着输入变量的变化而变化的函数。在本节中，我们将介绍如何计算 SymPy 中函数的导数和积分。

导数

函数的导数描述了它在给定点的变化率。在 SymPy 中，我们可以使用 sympy.diff 或者使用SymPy表达式实例的 diff 方法，来计算函数的导数。这些函数将一个符号或多个符号作为参数，函数或表达式将针对该符号进行求导。为了表示抽象函数 $f(x)$ 关于 x 的一阶导数，我们可以这样做

In [16]: f = sympy.Function('f')(x)

In [17]: sympy.diff(f, x)
Out[17]:
d
──(f(x))
dx

为了表示高阶导数，我们需要在 sympy.diff 的参数列表中重复符号 x，或者等价地通过在符号后指定一个整数作为参数，该参数定义了表达式中相应符号需要求导的次数：

In [18]: sympy.diff(f, x, x)
Out[18]:
  2
 d
───(f(x))
  2
dx

In [19]: sympy.diff(f, x, 3)
Out[19]:
  3
 d
───(f(x))
  3
dx

这种方法很容易扩展到多元函数：

In [20]: g = sympy.Function('g')(x, y)

In [21]: g.diff(x, y)
Out[21]:
   2
  ∂
─────(g(x, y))
∂y ∂x

In [23]: g.diff(x, 3, y, 2)
Out[23]:
    5
   ∂
───────(g(x, y))
  2   3
∂y  ∂x

迄今为止，这些例子只涉及未定义函数的求导。我们也可以计算已定义函数和表达式的导数。使用 sympy.diff 我们可以轻松计算任意数学表达式的导数。

In [24]: expr = x**4 + x**3 + x**2 + x + 1

In [25]: expr.diff(x)
Out[25]:
   3      2
4⋅x  + 3⋅x  + 2⋅x + 1

In [26]: expr.diff(x, x)
Out[26]:
  ⎛   2          ⎞
2⋅⎝6⋅x  + 3⋅x + 1⎠

In [27]: expr = (x + 1) ** 3 * y ** 2 *(z - 1)

In [28]: expr.diff(x, y, z)
Out[28]:
           2
6⋅y⋅(x + 1)

也能计算三角函数及其他复杂的数学表达式：

In [29]: expr = sympy.sin(x * y) * sympy.cos(x / 2)

In [30]: expr.diff(x)
Out[30]:
                       ⎛x⎞
                    sin⎜─⎟⋅sin(x⋅y)
     ⎛x⎞               ⎝2⎠
y⋅cos⎜─⎟⋅cos(x⋅y) - ───────────────
     ⎝2⎠                   2

In [31]: expr = sympy.special.polynomials.hermite(x, 0)

In [32]: expr.diff(x).doit()
Out[32]:
 x             ⎛     x   1⎞
2 ⋅√π⋅polygamma⎜0, - ─ + ─⎟    x
               ⎝     2   2⎠   2 ⋅√π⋅log(2)
─────────────────────────── + ────────────
           ⎛  x   1⎞            ⎛  x   1⎞
        2⋅Γ⎜- ─ + ─⎟           Γ⎜- ─ + ─⎟
           ⎝  2   2⎠            ⎝  2   2⎠

请注意，在上述示例中，直接调用表达式 sympy.diff 会产生新的表达式。如果我们想要符号化地表示一个定义表达式的导数，可以创建类 sympy.Derivative 的实例：

In [33]: d = sympy.Derivative(sympy.exp(sympy.cos(x)), x)

In [34]: d
Out[34]:
d ⎛ cos(x)⎞
──⎝ℯ      ⎠
dx

然后可以通过调用 sympy.Ditivative 实例的 doit 方法来计算此表达式的导数形式。

In [35]: d.doit()
Out[35]:
  cos(x)
-ℯ      ⋅sin(x)

这种延迟计算模式贯穿整个 SymPy，当需要将结果表示为形式表达式进行简化或操纵时，这种操作十分有用。

积分

在 SymPy 中，使用函数 sympy.integrate 计算积分，使用 sympy.Integral （与 sympy.Derviative 类似，可以通过调用 doit 方法显式计算）表示积分。SymPy 使用 sympy.integrate 函数处理定积分和不定积分。

如果只用表达式作为参数调用 sympy.integrate 函数，则计算不定积分。如果传递一个额外的元组参数，则计算定积分，元组形如 (x, a, b) ，其中 x 是积分变量，a 和 b 是积分限。对于单变量函数 f(x)，使用下式计算不定积分和定积分：

In [36]: a, b, x, y = sympy.symbols("a, b, x, y")

In [37]: f = sympy.Function("f")(x)

In [38]: sympy.integrate(f)
Out[38]:
⌠
⎮ f(x) dx
⌡

In [39]: sympy.integrate(f, (x, a, b))
Out[39]:
b
⌠
⎮ f(x) dx
⌡
a

当这些方法被应用到显式函数时，积分则进行相应地计算：

In [40]: sympy.integrate(sympy.sin(x))
Out[40]: -cos(x)

In [41]: sympy.integrate(sympy.sin(x), (x, a, b))
Out[41]: cos(a) - cos(b)

使用 SymPy 的无穷符号 oo，亦可使定积分的积分限包含正无穷或/和负无穷。

In [42]: sympy.integrate(sympy.exp(-x ** 2), (x, 0, oo))
Out[42]:
√π
──
2

In [43]: a, b, c = sympy.symbols("a, b, c", positive=True)

In [44]: sympy.integrate(a * sympy.exp(-((x - b)/c)**2), (x, -oo, oo))
Out[44]: √π⋅a⋅c

计算符号化积分通常十分困难，SymPy 不能给出积分的符号化结果。当 SymPy 不能计算一个积分时，会返回一个 sympy.Integral 实例，代表形式积分。

In [45]: sympy.integrate(sympy.sin(x * sympy.cos(x)))
Out[45]:
⌠
⎮ sin(x⋅cos(x)) dx
⌡

使用 sympy.integrate 亦可计算多元表达式。对于多元表达式的不定积分，积分变量需要指定：

In [46]: expr = sympy.sin(x * sympy.exp(y))

In [47]: sympy.integrate(expr, x)
Out[47]:
  -y    ⎛   y⎞
-ℯ  ⋅cos⎝x⋅ℯ ⎠

In [48]: expr = (x + y) ** 2

In [49]: sympy.integrate(expr, x)
Out[49]:
 3
x     2        2
── + x ⋅y + x⋅y
3

通过传递多个符号或者元组，我们可以计算多重积分：

In [50]: sympy.integrate(expr, x, y)
Out[50]:
 3      2  2      3
x ⋅y   x ⋅y    x⋅y
──── + ───── + ────
 3       2      3

In [51]: sympy.integrate(expr, (x, 0, 1), (y, 0, 1))
Out[51]: 7/6

级数

级数展开是许多计算领域的重要工具。通过级数展开，可以将任意函数写成一个多项式，其系数由该函数的导数在展开所围绕的点处给出。通过将级数展开成 n 阶，就可以得到函数的第 n 阶近似。在 SymPy 中，可以使用 sympy.series 函数或 SymPy 表达式实例中的 series 方法来计算函数或表达式的级数展开。
sympy.series 的第一个参数是要展开的函数或表达式，后面要计算展开的符号（对于单变量表达式和函数可以省略）。另外，还可以指定点来执行展开（使用 x0 关键字参数，默认 x0=0）、指定展开阶数（使用 n 关键字参数，默认值 n=6）、指定级数计算的方向，即从 x0 的下或上开始（使用 dir 关键字参数，默认为 dir='+'）。

In [52]: x = sympy.Symbol("x")

In [53]: f = sympy.Function("f")(x)

In [54]: sympy.series(f, x)
Out[54]:
                             ⎛  2      ⎞│         ⎛  3      ⎞│         ⎛  4
                           2 ⎜ d       ⎟│       3 ⎜ d       ⎟│       4 ⎜ d
                          x ⋅⎜───(f(x))⎟│      x ⋅⎜───(f(x))⎟│      x ⋅⎜───(f(
                             ⎜  2      ⎟│         ⎜  3      ⎟│         ⎜  4
         ⎛d       ⎞│         ⎝dx       ⎠│x=0      ⎝dx       ⎠│x=0      ⎝dx
f(0) + x⋅⎜──(f(x))⎟│    + ────────────────── + ────────────────── + ──────────
         ⎝dx      ⎠│x=0           2                    6                    24

   ⎞│         ⎛  5      ⎞│
   ⎟│       5 ⎜ d       ⎟│
x))⎟│      x ⋅⎜───(f(x))⎟│
   ⎟│         ⎜  5      ⎟│
   ⎠│x=0      ⎝dx       ⎠│x=0    ⎛ 6⎞
──────── + ────────────────── + O⎝x ⎠

指定在 $x_0$ 处展开：

In [58]: x0 = sympy.Symbol("x_0")

In [60]: f.series(x, x0, n=2)
Out[60]:
                 ⎛ d        ⎞│         ⎛        2        ⎞
f(x₀) + (x - x₀)⋅⎜───(f(ξ₁))⎟│      + O⎝(x - x₀) ; x → x₀⎠
                 ⎝dξ₁       ⎠│ξ₁=x₀

这里我们也指定了 n=2，要求级数只进行二阶展开。由于截断而产生的误差使用 $O(...)$ 表示。在数值计算时，需要删除误差项，这时可以使用 removeO 方法：

In [61]: f.series(x, x0, n=2).removeO()
Out[61]:
         ⎛ d        ⎞│
(x - x₀)⋅⎜───(f(ξ₁))⎟│      + f(x₀)
         ⎝dξ₁       ⎠│ξ₁=x₀

可以很容易地获得标准数学函数的展开：

In [62]: sympy.cos(x).series()
Out[62]:
     2    4
    x    x     ⎛ 6⎞
1 - ── + ── + O⎝x ⎠
    2    24

In [63]: sympy.sin(x).series()
Out[63]:
     3     5
    x     x     ⎛ 6⎞
x - ── + ─── + O⎝x ⎠
    6    120

In [64]: sympy.exp(x).series()
Out[64]:
         2    3    4     5
        x    x    x     x     ⎛ 6⎞
1 + x + ── + ── + ── + ─── + O⎝x ⎠
        2    6    24   120

In [65]: (1/(1+x)).series()
Out[65]:
         2    3    4    5    ⎛ 6⎞
1 - x + x  - x  + x  - x  + O⎝x ⎠

当然，任意表达式和函数亦可展开：

In [66]: expr = sympy.cos(x) / (1 + sympy.sin(x * y))

In [67]: expr.series(x, n=4)
Out[67]:
                           ⎛     3    ⎞
           2 ⎛ 2   1⎞    3 ⎜  5⋅y    y⎟    ⎛ 4⎞
1 - x⋅y + x ⋅⎜y  - ─⎟ + x ⋅⎜- ──── + ─⎟ + O⎝x ⎠
             ⎝     2⎠      ⎝   6     2⎠

In [68]: expr.series(y, n=4)
Out[68]:
                                        3  3
                       2  2          5⋅x ⋅y ⋅cos(x)    ⎛ 4⎞
cos(x) - x⋅y⋅cos(x) + x ⋅y ⋅cos(x) - ────────────── + O⎝y ⎠

极限

微积分的另一个重要工具是极限。可以使用 sympy.limit 函数计算极限：

1 2	In [69]: sympy.limit(sympy.sin(x)/x, x, 0) Out[69]: 1

也可以使用它计算符号极限：

In [70]: f = sympy.Function('f')

In [71]: x, h = sympy.symbols("x, h")

In [72]: diff_limit = (f(x + h) - f(x)) / h

In [73]: sympy.limit(diff_limit.subs(f, sympy.cos), h, 0)
Out[73]: -sin(x)

In [74]: sympy.limit(diff_limit.subs(f, sympy.sin), h, 0)
Out[74]: cos(x)

另一个更实际的例子是使用极限发现函数的渐近行为，考虑函数 $f(x) = (x^3-3x)/(2x-2)$ ，当 x 增大， $f(x) \to px+q$ 。这里我们使用 sympy.limit 计算 p、q。

In [75]: expr = (x**2 - 3*x) / (2*x -2)

In [79]: p = sympy.limit(expr/x, x, oo)

In [81]: q = sympy.limit(expr-p*x, x, oo)

In [82]: p, q
Out[82]: (1/2, -1)

和与积

和与积使用 sympy.Sum 与 sympy.Product 函数表示，使用 doit 方法计算。

In [83]: n = sympy.symbols('n', integer=True)

In [84]: x = sympy.Sum(1/(n**2), (n, 1, oo))

In [85]: x
Out[85]:
  ∞
 ____
 ╲
  ╲   1
   ╲  ──
   ╱   2
  ╱   n
 ╱
 ‾‾‾‾
n = 1

In [86]: x.doit()
Out[86]:
 2
π
──
6

In [87]: x = sympy.Product(n, (n, 1, 7))

In [88]: x
Out[88]:
  7
┬───┬
│   │ n
│   │
n = 1

In [89]: x.doit()
Out[89]: 5040

上式求和上限为无穷大，其结果显然是通过分析方法计算出来的。SymPy 能够提供这种类型的符号化结果。

In [90]: x = sympy.Symbol("x")

In [92]: sympy.Sum((x)**n/(sympy.factorial(n)), (n, 1, oo)).doit().simplify()
Out[92]:
 x
ℯ  - 1

方程

方程求解是数学的一个基本部分，几乎在所有科学和技术领域都有应用，因此非常重要。SymPy 可以符号化地解各种各样的方程，即使原则上许多方程无解析解。如果一个方程或一个系统或方程组有解析解，那么 SymPy 很有可能找到解。如果没有，则提供数值解。

在 SymPy 中，我们可以使用函数 sympy.solve 来找满足方程的解，如：对于方程 $x^2+2x-3=0$ 。

In [94]: x = sympy.Symbol("x")

In [95]: sympy.solve(x**2 + x*2 - 3)
Out[95]: [-3, 1]

sympy.solve 基于方程等于零的假设给出解。当包含多个符号时，必须指出需要求解的符号：

In [97]: sympy.solve(a * x **2 + b * x + c, x)
Out[97]:
⎡        _____________   ⎛       _____________⎞ ⎤
⎢       ╱           2    ⎜      ╱           2 ⎟ ⎥
⎢-b + ╲╱  -4⋅a⋅c + b    -⎝b + ╲╱  -4⋅a⋅c + b  ⎠ ⎥
⎢─────────────────────, ────────────────────────⎥
⎣         2⋅a                     2⋅a           ⎦

sympy.solve 也能求解三角表达式，

In [98]: sympy.solve(sympy.sin(x) - sympy.cos(x), x)
Out[98]:
⎡-3⋅π   π⎤
⎢─────, ─⎥
⎣  4    4⎦

以及其解可以用特殊函数表示的等式：

1 2	In [99]: sympy.solve(sympy.exp(x) + 2*x, x) Out[99]: [-LambertW(1/2)]

然而，在处理一般方程时，即使是单变量情况下，遇到无代数解或者 SymPy 无法求解的方程也是常见的。在这些情况下，如果可以通过数值方法进行评估，SymPy 将返回一个形式解，如果没有方法可用于特定类型的方程，则会引发错误：

In [100]: sympy.solve(x**5 -x**2 +1, x)
Out[100]:
⎡       ⎛ 5    2       ⎞         ⎛ 5    2       ⎞         ⎛ 5    2       ⎞
⎣CRootOf⎝x  - x  + 1, 0⎠, CRootOf⎝x  - x  + 1, 1⎠, CRootOf⎝x  - x  + 1, 2⎠, CR

     ⎛ 5    2       ⎞         ⎛ 5    2       ⎞⎤
ootOf⎝x  - x  + 1, 3⎠, CRootOf⎝x  - x  + 1, 4⎠⎦

In [101]: sympy.solve(sympy.tan(x) + x, x)
---------------------------------------------------------------------------
NotImplementedError                       Traceback (most recent call last)
<ipython-input-101-f0d1216e07b0> in <module>()
----> 1 sympy.solve(sympy.tan(x) + x, x)

[... ...]

NotImplementedError: multiple generators [x, tan(x)]
No algorithms are implemented to solve equation x + tan(x)

多变量方程的求解：

In [102]: eq1 = x + 2*y - 1

In [103]: eq2 = x - y + 1

In [104]: sympy.solve([eq1, eq2], [x, y], dict=True)
Out[104]: [{x: -1/3, y: 2/3}]

In [105]: eq1 = x**2 - y

In [106]: eq2 = y**2 - x

In [107]: sols = sympy.solve([eq1, eq2], [x, y], dict=True)

In [108]: sols
Out[108]:
⎡                            ⎧               2               ⎫  ⎧
⎢                            ⎪   ⎛  1   √3⋅ⅈ⎞        1   √3⋅ⅈ⎪  ⎪   ⎛  1   √3⋅
⎢{x: 0, y: 0}, {x: 1, y: 1}, ⎨x: ⎜- ─ - ────⎟ , y: - ─ - ────⎬, ⎨x: ⎜- ─ + ───
⎢                            ⎪   ⎝  2    2  ⎠        2    2  ⎪  ⎪   ⎝  2    2
⎣                            ⎩                               ⎭  ⎩

  2               ⎫⎤
ⅈ⎞        1   √3⋅ⅈ⎪⎥
─⎟ , y: - ─ + ────⎬⎥
 ⎠        2    2  ⎪⎥
                  ⎭⎦

在上式中使用了可选参数 dict=True ，字典格式可以很容易验证解是否符合条件：

1 2	In [109]: [eq1.subs(sol).simplify() == 0 and eq2.subs(sol).simplify() == 0 for sol in sols] Out[109]: [True, True, True, True]

线性代数

线性代数是数学的另一个基本分支，在科学和技术计算中有重要应用。它涉及向量、向量空间以及向量空间之间的线性映射（这些映射可以表示为矩阵）。在 SymPy 中，我们可以使用 sympy.Matrix 类来符号化地表示向量和矩阵，其中元素可以用数字、符号甚至任意符号表达式来表示。要创建一个包含数值的矩阵，可以将一个 Python 列表传递给 sympy.Matrix：

In [110]: sympy.Matrix([1, 2])
Out[110]:
⎡1⎤
⎢ ⎥
⎣2⎦

In [111]: sympy.Matrix([[1, 2]])
Out[111]: [1  2]

In [112]: sympy.Matrix([[1, 2], [3, 4]])
Out[112]:
⎡1  2⎤
⎢    ⎥
⎣3  4⎦

创建新的 sympy.Matrix 对象的另一种方法是传递行数、列数以及处理函数（该函数将行列索引作为参数，返回相应位置元素的值）作为参数：

In [113]: sympy.Matrix(3, 4, lambda m, n: 10 * m + n)
Out[113]:
⎡0   1   2   3 ⎤
⎢              ⎥
⎢10  11  12  13⎥
⎢              ⎥
⎣20  21  22  23⎦

SymPy 矩阵强大之处在于它能将符号表达式作为元素，这也是它与 NumPy 数组的区别之处。

In [114]: a, b, c, d = sympy.symbols("a, b, c, d")

In [115]: M = sympy.Matrix([[a, b], [c, d]])

In [116]: M
Out[116]:
⎡a  b⎤
⎢    ⎥
⎣c  d⎦

这样的矩阵也能进行计算：

In [117]: M * M
Out[117]:
⎡ 2                  ⎤
⎢a  + b⋅c   a⋅b + b⋅d⎥
⎢                    ⎥
⎢                  2 ⎥
⎣a⋅c + c⋅d  b⋅c + d  ⎦

In [118]: x = sympy.Matrix(sympy.symbols("x_1, x_2"))

In [119]: x
Out[119]:
⎡x₁⎤
⎢  ⎥
⎣x₂⎦

In [120]: M * x
Out[120]:
⎡a⋅x₁ + b⋅x₂⎤
⎢           ⎥
⎣c⋅x₁ + d⋅x₂⎦

除了算术运算外，向量和矩阵上的许多标准线性代数运算也作为 sympy.Matrix 类的 SymPy 函数和方法实现了。下表给出了常用的线性代数相关函数的总结。SymPy 矩阵也可以使用索引和切片操作。

函数/方法	描述
transpose/ T	计算矩阵的转置
adjoint/ H	计算矩阵的伴随阵
trace	计算矩阵的迹（对角线元素的总和）
det	计算矩阵的行列式
inv	计算矩阵的逆
LUdecomposition	计算矩阵的 LU 分解
LUsolve	使用 LU 分解法，求解形如 `Mx=b` 的等式，其中 x 是未知向量
QRdecomposition	计算矩阵的 QR 分解
QRsolve	使用 QR 分解法求解形如 `Mx=b` 的线性方程组，其中 x 是未知向量
diagonalize	使矩阵 M 对角化
norm	计算矩阵的范数
nullspace	计算矩阵零空间的一组向量
rank	计算矩阵的秩
singular_values	计算矩阵的奇异值
solve	求解形如 `Mx=b` 的线性方程组

考虑以下参数线性方程组，其不能直接使用纯数值方法解，但可以使用符号求解：

$$
\begin{array}{c}
x + py &= b_1, \
qx + y &= b_2,
\end{array}
$$

其矩阵形式：

$$
\begin{pmatrix}
1 &p \
q &1 \
\end{pmatrix}
\begin{pmatrix}
x \
y \
\end{pmatrix}
=
\begin{pmatrix}
b_1 \
b_2 \
\end{pmatrix}
$$

使用纯数值方法，在解这个问题之前，我们必须选择参数 p 和 q 的值。使用符号计算方法，我们可以直接计算解。使用 SymPy，我们可以简单地为未知变量和参数定义符号，并设置所需的矩阵对象：

In [121]: p, q = sympy.symbols("p, q")

In [122]: M = sympy.Matrix([[1, p], [q, 1]])

In [123]: M
Out[123]:
⎡1  p⎤
⎢    ⎥
⎣q  1⎦

In [124]: b = sympy.Matrix(sympy.symbols("b_1, b_2"))

In [125]: b
Out[125]:
⎡b₁⎤
⎢  ⎥
⎣b₂⎦

使用 LUsolve 方法解该线性方程组：

In [126]: x = M.LUsolve(b)

In [127]: x
Out[127]:
⎡     p⋅(-b₁⋅q + b₂)⎤
⎢b₁ - ──────────────⎥
⎢        -p⋅q + 1   ⎥
⎢                   ⎥
⎢    -b₁⋅q + b₂     ⎥
⎢    ──────────     ⎥
⎣     -p⋅q + 1      ⎦

也可以直接计算矩阵的逆，然后乘上向量 b：

In [128]: x = M.inv() * b

In [129]: x
Out[129]:
⎡    b₁        b₂⋅p   ⎤
⎢ ──────── - ──────── ⎥
⎢ -p⋅q + 1   -p⋅q + 1 ⎥
⎢                     ⎥
⎢    b₁⋅q        b₂   ⎥
⎢- ──────── + ────────⎥
⎣  -p⋅q + 1   -p⋅q + 1⎦

计算矩阵的逆矩阵比执行 LU 分解更困难，所以使用 LU 分解更有效率。对于较大的方程系统而言，这变得特别明显。在这里考虑了两种方法，解的符号表达式法，对于任何参数值都无需重新计算解，这是符号计算的优势。

本文翻译自：R. Johansson, Numerical Python.