经典CS问题Python实现：搜索问题

发表于 更新于 阅读次数：

“搜索”是一个如此宽泛的术语，以至于整系列都可以被称为Python中的经典搜索问题。本章是关于每个程序员都应该知道的核心搜索算法。尽管有宣言式的标题，但并不表明是全面的。

DNA搜索

基因在计算机软件中通常可表示为字符A、C、G和T的序列。每个字母代表一个核苷酸（nucleotide），三个核苷酸的组合被称为密码子（codon）。如图所示。一个密码子编码一个特定的氨基酸（amino acids），和其他氨基酸一起可以形成一个蛋白质（protein）。生物信息学软件中的一个经典任务是找到基因中的一个特定密码子。

部分基因

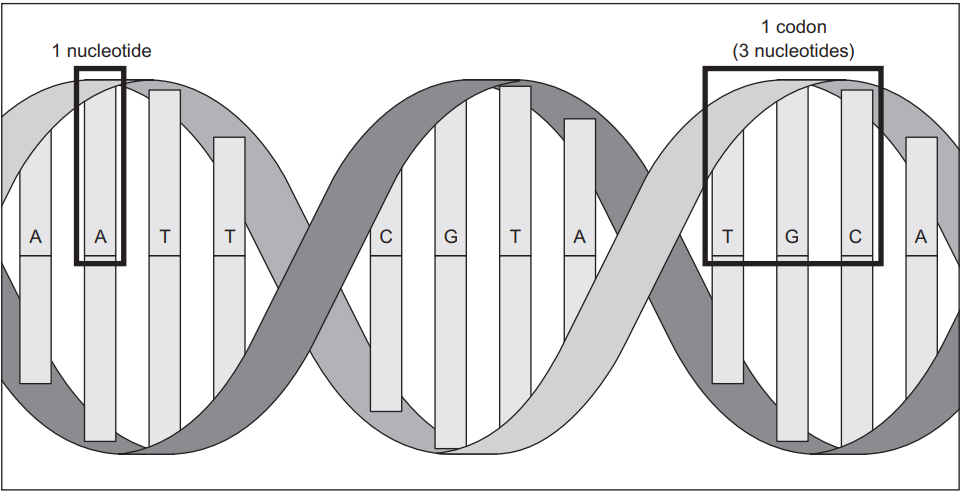
存储DNA

我们可以将核苷酸的四种情况表示为一个简单的IntEnum。

清单1 dna_search.py

1
2
3
4
from enum import IntEnum
from typing import Tuple, List

Nucleotide: IntEnum = IntEnum('Nucleotide', ('A', 'C', 'G', 'T'))

Nucleotide的类型是IntEum，而不仅仅是Enum，因为IntEum“免费”为我们提供了比较运算符（<、>和=等等），为了让搜索算法能够对其进行操作，需要在数据类型中包含这些运算符。Tuple和List是从typing包中导入的，以辅助类型提示。

密码子可定义为三个Nucleotide的元组，基因可表示为Codon列表。

清单2 dna_search.py 续

1
2
Codon = Tuple[Nucleotide, Nucleotide, Nucleotide] # type alias for codons
Gene = List[Codon] # type alias for genes

注 虽然我们以后需要进行Codon之间的比较，但是不需要定义一个显式实现<操作符的Codon定制类。这是因为Python内置了对元组之间比较的支持，如果元组由同样具有可比性的类型组成。

一般来说，互联网上的基因将会有一个文件格式，包含一个代表基因序列中所有核苷酸的巨型字符串。我们为一个假想的基因定义这样一个字符串，称之为gene_str。

清单3 dna_search.py 续

1
gene_str: str = "ACGTGGCTCTCTAACGTACGTACGTACGGGGTTTATATATACCCTAGGACTCCCTTT"

我们需要一个工具函数将str转换为Gene。

清单4 dna_search.py 续

1
2
3
4
5
6
7
8
9
def string_to_gene(s: str) -> Gene:
    gene: Gene = []
    for i in range(0, len(s), 3):
        if (i + 2) >= len(s): # don't run off end!
            return gene
        # initialize codon out of three nucleotides
        codon: Codon = (Nucleotide[s[i]], Nucleotide[s[i + 1]], Nucleotide[s[i + 2]])
        gene.append(codon) # add codon to gene
    return gene

string_to_gene()会不断地遍历所提供的str，并将其后面的三个字符转换为密码子，然后添加到新Gene的末尾。如果发现在接下来的两个位置没有Nucleotide（见循环中的if语句），那么表明已经到达了一个不完整基因的末端，并跳过最后一个或两个核苷酸。

string_to_gene()可用于将str gene_str转换为Gene。

清单5 dna_search.py 续

1
my_gene: Gene = string_to_gene(gene_str)

线性搜索

我们可能想到的对基因进行的一个基本操作是搜索它的特定密码子。目标是简单地找出密码子是否存在于基因中。

线性搜索按照原始数据结构的顺序遍历搜索空间中的每个元素，直到找到所要搜索的内容或到达数据结构的末尾。实际上，线性搜索是最简单、最自然、最明显的搜索方式。在最坏的情况下，线性搜索将需要遍历数据结构中的每一个元素，因此它具有O(n)复杂度，其中n是结构中元素的数量，如图所示。

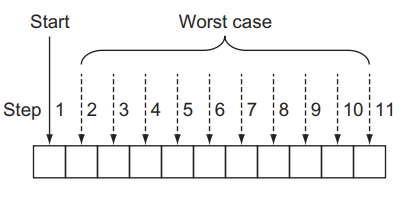
线性搜索最坏情况

定义一个执行线性搜索的函数很简单。它遍历数据结构中的每一个元素，并检查该元素是否与要查找的项等价。下面的代码为Gene和Codon定义了这样一个函数，然后对my_gene和Codon acg和gat进行了测试。

清单6 dna_search.py 续

1
2
3
4
5
6
7
8
9
10
def linear_contains(gene: Gene, key_codon: Codon) -> bool:
    for codon in gene:
        if codon == key_codon:
            return True
        return False

acg: Codon = (Nucleotide.A, Nucleotide.C, Nucleotide.G)
gat: Codon = (Nucleotide.G, Nucleotide.A, Nucleotide.T)
print(linear_contains(my_gene, acg)) # True
print(linear_contains(my_gene, gat)) # False

注 该函数仅用于说明目的。Python内置的序列类型（list、tuple和range）都实现了__contains__()方法，该方法允许我们通过简单地使用in运算符来搜索其中的特定项。事实上，in运算符可以与任何实现__contains__()的类型一起使用。例如，我们可以在my_gene中搜索acg，并通过print(acg in my_gene)输出结果。

二分搜索

有一种比查看每个元素更快的搜索方式，但要求我们提前了解数据结构的顺序。如果结构已经排序，且可以通过索引立即访问其中的任何项，我们就可以执行二分搜索。基于这一准则，已排序的Pythonlist是二分搜索的最佳选择。

二分搜索的原理是观察元素排序范围内的中间元素，将其与所查找的元素进行比较，根据比较结果将范围缩小一半，然后重新开始该过程。让我们看一个具体的例子。

假设我们有一个按字母顺序排序的单词list，如["cat", "dog", "kangaroo", "llama", "rabbit", "rat", "zebra"]，查找单词“rat”：

  1. 确定这个七个单词列表中的中间元素是“llama”；
  2. 确定“rat”按字母顺序排在“llama”之后，所以它必须在“llama”之后的列表的（大约）一半中（如果在这一步找到了“rat”，就可以返回它的位置；如果发现“rat”在我们检查的中间单词之前，我们可以确定它在“llama”之后的列表的一半中）；
  3. 对“rat”可能仍在的列表的一半重新运行步骤1和2。实际上，这一半成了新的基本列表。这些步骤持续进行，直到找到“rat”或者正在查找的范围不再包含任何要搜索的元素，这意味着单词列表中不存在“rat”。

下图展示了二分搜索。需要注意的是，与线性搜索不同，二分搜索不涉及检查每个元素。

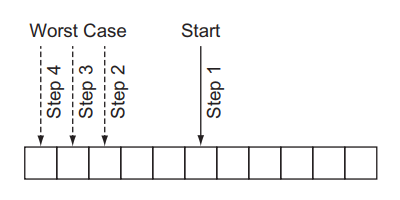
二分搜索最坏情况

二分搜索不断地将搜索空间减少一半，因此它的最坏运行时间为O(lg n)。不过，还是有一个陷阱。与线性搜索不同，二分搜索需要经过排序的数据结构来搜索，排序需要时间。事实上，对于最好的排序算法来说，排序需要花费O(n lg n)时间。如果我们只运行一次搜索，并且我们的原始数据结构没有排序，那么只进行线性搜索可能是有意义的。但是，如果搜索要执行多次，那么这样做的时间成本是值得的，因为这样可以大大减少每次搜索的时间成本。

为基因和密码子编写二分搜索与为任何其他类型的数据编写二分搜索函数没有什么不同，因为Codon类型可以与其他类型进行比较，而Gene类型只是一个list。

清单7 dna_search.py 续

1
2
3
4
5
6
7
8
9
10
11
12
def binary_contains(gene: Gene, key_codon: Codon) -> bool:
    low: int = 0
    high: int = len(gene) - 1
    while low <= high: # while there is still a search space
        mid: int = (low + high) // 2
        if gene[mid] < key_codon:
            low = mid + 1
        elif gene[mid] > key_codon:
            high = mid - 1
        else:
            return True
    return False

让我们一行一行地浏览这个函数。

1
2
low: int = 0
high: int = len(gene) - 1

我们从一个包含整个列表（gene）的范围开始。

1
while low <= high:

只要还有搜索范围，我们就会继续搜索。当low大于high时，意味着列表中不再有任何可查看的位置。

1
mid: int = (low + high) // 2

我们用整数除法和你在小学学到的简单平均公式来计算mid。

1
2
if gene[mid] < key_codon:
    low = mid + 1

如果寻找的元素在寻找的范围的中间元素之后，需要修改循环中下次迭代的范围，将low移动到当前中间元素之后。这是下一次迭代范围减半的地方。

1
2
elif gene[mid] > key_codon:
    high = mid - 1

同样，当我们寻找的元素小于中间元素时，我们在另一个方向减半。

1
2
else:
    return True

如果所讨论的元素不小于或大于中间元素，这意味着我们找到了它！当然，如果循环没有迭代，我们返回False（这里没有重现），表明它从未被发现。

我们可以尝试用相同的基因和密码子来运行我们的函数，但是我们必须记住先排序。

清单8 dna_search.py 续

1
2
3
my_sorted_gene: Gene = sorted(my_gene)
print(binary_contains(my_sorted_gene, acg)) # True
print(binary_contains(my_sorted_gene, gat)) # False

提示 可以使用Python标准库的bisect模块：https://docs.python.org/3/library/bisect.html 来构建一个高效的二分搜索。

一般性例子

函数linear_contains()和binary_contains()可以推广到几乎任何Python序列。以下通用版本与之前看到的版本几乎相同，只是一些名称和类型提示有所更改。

注 在下面的代码列表中有许多导入的类型。在本章中，我们将为许多进一步的通用搜索算法重用generic_search.py文件，这样就不会妨碍导入。

注 在继续阅读之前，你需要通过pip install typing_extensions或pip3 install typing_extensions来安装typing_extensions模块，这取决于你的Python解释器是如何配置的。需要这个模块来访问Protocol类型，它将在Python的未来版本的标准库中（由PEP 544指定）。因此，在Python的未来版本中，导入type_extensions模块应该是不必要的，并且你可以使用from typing import Protocol而不是from typing_extensions import Protocol。

清单9 generic_search.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
from __future__ import annotations
from typing import TypeVar, Iterable, Sequence, Generic, List, Callable, Set, Deque, Dict, Any, Optional
from typing_extensions import Protocol
from heapq import heappush, heappop

T = TypeVar('T')

def linear_contains(iterable: Iterable[T], key: T) -> bool:
    for item in iterable:
        if item == key:
            return True
    return False

C = TypeVar("C", bound="Comparable")

class Comparable(Protocol):
    def __eq__(self, other: Any) -> bool:
        ...
    def __lt__(self: C, other: C) -> bool:
        ...
    def __gt__(self: C, other: C) -> bool:
        return (not self < other) and self != other
    def __le__(self: C, other: C) -> bool:
        return self < other or self == other
    def __ge__(self: C, other: C) -> bool:
        return not self < other

def binary_contains(sequence: Sequence[C], key: C) -> bool:
    low: int = 0
    high: int = len(sequence) - 1
    while low <= high: # while there is still a search space
        mid: int = (low + high) // 2
        if sequence[mid] < key:
            low = mid + 1
        elif sequence[mid] > key:
            high = mid - 1
        else:
            return True
    return False


if __name__ == "__main__":
    print(linear_contains([1, 5, 15, 15, 15, 15, 20], 5)) # True
    print(binary_contains(["a", "d", "e", "f", "z"], "f")) # True
    print(binary_contains(["john", "mark", "ronald", "sarah"], "sheila")) # False

现在，可以尝试对其他类型的数据进行搜索。几乎所有的Python集合都可以重用这些函数。这就是通用代码的力量。这个例子中唯一不幸的元素是Python的类型提示必须跳过的复杂的环，通过Comparable类的形式。Comparable类型是实现比较运算符的类型。在Python的未来版本中，应该有一种更简洁的方法来为实现这些常见运算符的类型创建类型提示。

求解迷宫问题

在迷宫中寻找路径类似于计算机科学中许多常见的搜索问题。那么，为什么不从字面上找到一条穿过迷宫的路径，来说明广度优先搜索、深度优先搜索和A*算法呢？

我们的迷宫将是Cell的二维网格。Cell是一个包含str值的枚举，其中“ ”表示空白，而“X”表示被阻止的空间。在打印迷宫时，还有其他一些示例。

清单10 maze.py

1
2
3
4
5
6
7
8
9
10
11
12
from enum import Enum
from typing import List, NamedTuple, Callable, Optional
import random
from math import sqrt
from generic_search import dfs, bfs, node_to_path, astar, Node

class Cell(str, Enum):
    EMPTY = " "
    BLOCKED = "X"
    START = "S"
    GOAL = "G"
    PATH = "*"

我们又一次开始大量导入。需要注意的是，最后一个导入（从generic_search）是我们尚未定义的符号。为了方便起见，这里包含了它，要对它进行注释，直到需要它为止。

我们需要一种方法来引用迷宫中的一个单独的位置。这里是一个简单的NamedTuple，其属性代表所讨论位置的行和列。

清单11 maze.py 续

1
2
3
class MazeLocation(NamedTuple):
    row: int
    column: int

产生随机迷宫

Maze类在内部跟踪代表其状态的网格，有用于行数、列数、起始位置和目标位置的实例变量。其网格将随机填充阻塞单元。

生成的迷宫应该相当稀疏，这样从给定的起点位置到给定的目标位置几乎总是有一条路径（毕竟，是为了测试算法）。迷宫的稀疏度是可调节的，设置20%阻塞默认值。当一个随机数超过所讨论的sparseness的阈值时，我们将简单地用一堵“墙”来代替空的空间。如果我们对迷宫中的每一个可能的地方都这样做，从统计上来说，迷宫的稀疏性作为一个整体将接近所提供的sparseness。

清单12 maze.py 续

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Maze:
    def __init__(self, rows: int = 10, columns: int = 10, sparseness: float = 0.2, start: MazeLocation = MazeLocation(0, 0), goal: MazeLocation = MazeLocation(9, 9)) -> None:
        # initialize basic instance variables
        self._rows: int = rows
        self._columns: int = columns
        self.start: MazeLocation = start
        self.goal: MazeLocation = goal
        # fill the grid with empty cells
        self._grid: List[List[Cell]] = [[Cell.EMPTY for c in range(columns)] for r in range(rows)]
        # populate the grid with blocked cells
        self._randomly_fill(rows, columns, sparseness)
        # fill the start and goal locations in
        self._grid[start.row][start.column] = Cell.START
        self._grid[goal.row][goal.column] = Cell.GOAL
    def _randomly_fill(self, rows: int, columns: int, sparseness: float):
        for row in range(rows):
            for column in range(columns):
                if random.uniform(0, 1.0) < sparseness:
                    self._grid[row][column] = Cell.BLOCKED

现在我们有了一个迷宫，我们想要一种简单的方式把它打印到控制台上。我们希望它的字符靠得很近，这样它看起来就像一个真正的迷宫。

清单13 maze.py 续

1
2
3
4
5
6
# return a nicely formatted version of the maze for printing
def __str__(self) -> str:
    output: str = ""
    for row in self._grid:
        output += "".join([c.value for c in row]) + "\n"
    return output

现在，开始测试这些迷宫函数。

1
2
maze: Maze = Maze()
print(maze)

迷宫细节

稍后会有一个函数可检查在搜索过程中是否达到了目标。换句话说，我们想检查搜索是否达到了特定的MazeLocation。我们可以给Maze增加一个方法。

清单14 maze.py 续

1
2
def goal_test(self, ml: MazeLocation) -> bool:
    return ml == self.goal

那么，如何在迷宫中移动？假设我们在迷宫中特定位置每次水平和垂直地移动一格位置。使用这些标准，Successors()函数可以从给定的MazeLocation找到下一个可能的位置。然而，Successors()函数对于每个Maze都是不同的，因为每个Maze都有不同的大小和不同的墙。因此，我们将把它定义为Maze的一种方法。

清单15 maze.py 续

1
2
3
4
5
6
7
8
9
10
11
def successors(self, ml: MazeLocation) -> List[MazeLocation]:
    locations: List[MazeLocation] = []
    if ml.row + 1 < self._rows and self._grid[ml.row + 1][ml.column] != Cell.BLOCKED:
        locations.append(MazeLocation(ml.row + 1, ml.column))
    if ml.row - 1 >= 0 and self._grid[ml.row - 1][ml.column] != Cell.BLOCKED:
        locations.append(MazeLocation(ml.row - 1, ml.column))
    if ml.column + 1 < self._columns and self._grid[ml.row][ml.column + 1] != Cell.BLOCKED:
        locations.append(MazeLocation(ml.row, ml.column + 1))
    if ml.column - 1 >= 0 and self._grid[ml.row][ml.column - 1] != Cell.BLOCKED:
        locations.append(MazeLocation(ml.row, ml.column - 1))
    return locations

Successors()简单地检查Maze中MazeLocation的上、下、右和左，看是否能找到可以从此进入的空位置。它还避免检查Maze超出边缘的位置。它将找到的每一个可能的MazeLocation放入一个列表中，最终返回给调用者。

深度优先搜索

深度优先搜索（depth-first search，DFS）顾名思义就是：在回溯到最后一个决策点（如果到达死胡同）之前，尽可能深入的搜索。我们将实现一个通用的深度优先搜索，可以解决我们的迷宫问题。对于其他问题，它也是可重用的。下图显示了迷宫的深度优先搜索。

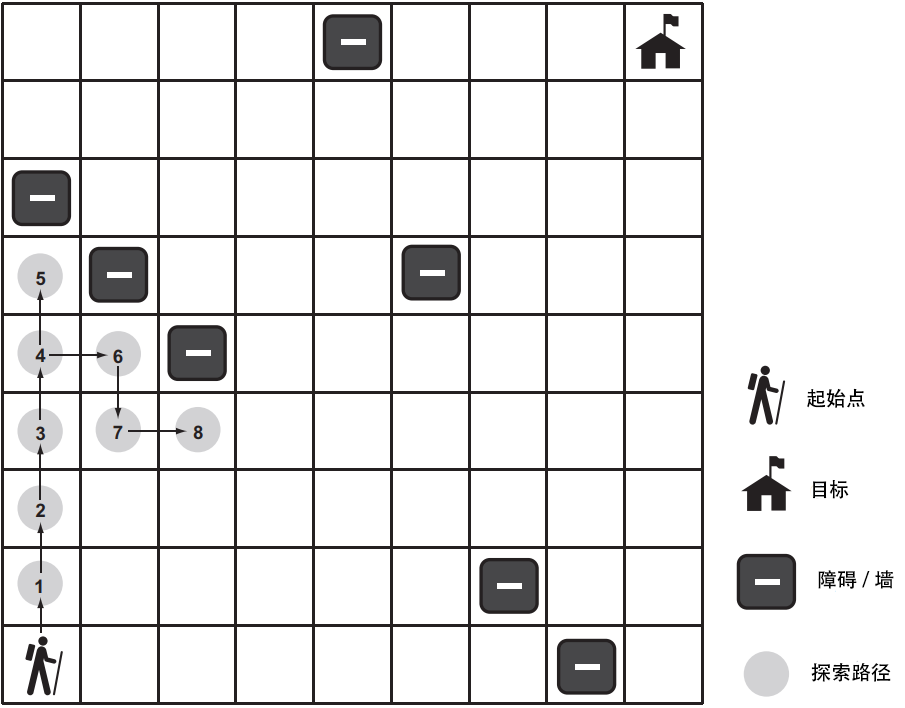
深度优先搜索

堆栈

深度优先搜索算法依赖于一种称为堆栈（stack）的数据结构。堆栈是在后进先出（Last-In-First-Out，LIFO）原则下运行的数据结构。想象一堆纸张，最后一张放上去的纸是第一张拿出来的纸。堆栈通常在更原始的数据结构（如列表）之上实现。我们将在Python的list类型之上实现我们的堆栈。

堆栈通常至少有两种操作：

  • push() 将元素放在堆栈顶部
  • pop() 从堆栈顶部移除并返回元素

我们将实现上述两种操作，以及实现一个空属性empty来检查堆栈中是否还有其他元素。我们把堆栈的代码添加到前面使用的generic_search.py文件中。我们已经完成了所有必要的导入。

清单16 generic_search.py 续

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Stack(Generic[T]):
    def __init__(self) -> None:
        self._container: List[T] = []
    
    @property
    def empty(self) -> bool:
        return not self._container # not is true for empty container
    
    def push(self, item: T) -> None:
        self._container.append(item)
    
    def pop(self) -> T:
        return self._container.pop() # LIFO
    
    def __repr__(self) -> str:
        return repr(self._container)

请注意，使用Python list实现的堆栈就像总是将元素附加到它的右端，并总是从它的右端移除元素。如果列表中不再有任何元素，list上的pop()方法将返回失败，因此如果Stack也为空，则pop()方法返回失败。

DFS算法

在我们开始实现DFS之前，我们还需要一个小细节。我们需要一个Node类，当搜索时，使用它来跟踪从一个状态到另一个状态的改变。可以将Node视为状态的包装器。就迷宫求解问题而言，这些状态属于MazeLocation类型。我们将节点Node称为来自其父节点parent的一种状态。我们还将为Node类添加cost和heuristic属性并实现__lt__()，这样就可以在后面的A*算法中重用它。

清单17 generic_search.py 续

1
2
3
4
5
6
7
8
9
class Node(Generic[T]):
    def __init__(self, state: T, parent: Optional[Node], cost: float = 0.0, heuristic: float = 0.0) -> None:
        self.state: T = state
        self.parent: Optional[Node] = parent
        self.cost: float = cost
        self.heuristic: float = heuristic

    def __lt__(self, other: Node) -> bool:
        return (self.cost + self.heuristic) < (other.cost + other.heuristic)

提示 Optional类型表示参数化类型的值可能被变量引用，或者变量可能引用None。

提示 在文件的头部，from future import annotations 允许Node在其方法的类型提示中引用自身。没有它，我们需要将类型提示作为字符串放在引号中（例如，’Node’）。在Python的未来版本中，导入annotations将是不必要的。

进行中的深度优先搜索需要跟踪两种数据结构：当前堆栈的状态（或者说“位置”），称之为前哨frontier；以及已经搜索过的状态集合，称之为explored。只要前哨还有状态可以访问，DFS将继续检查他们是否是目标（如果一个状态是目标，DFS将停止并返回），并将后继（successors）添加到前哨。DFS还会将已经搜索过的每个状态标记为已探索，这样搜索就不会陷入循环，将之前访问过的状态作为后继状态。如果前哨是空的，则意味着没有可供搜索的地方。

清单18 generic_search.py 续

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def dfs(initial: T, goal_test: Callable[[T], bool], successors: Callable[[T], List[T]]) -> Optional[Node[T]]:
    # frontier is where we've yet to go
    frontier: Stack[Node[T]] = Stack()
    frontier.push(Node(initial, None))
    # explored is where we've been
    explored: Set[T] = {initial}

    # keep going while there is more to explore
    while not frontier.empty:
        current_node: Node[T] = frontier.pop()
        current_state: T = current_node.state
        # if we found the goal, we're done
        if goal_test(current_state):
            return current_node
        # check where we can go next and haven't explored
        for child in successors(current_state):
            if child in explored: # skip children we already explored
                continue
            explored.add(child)
            frontier.push(Node(child, current_node))
    return None # went through everything and never found goal

如果dfs()成功，则返回封装目标状态的Node。从开始到目标的路径可以通过使用parent属性从该Node后向传递重建。

清单19 generic_search.py 续

1
2
3
4
5
6
7
8
def node_to_path(node: Node[T]) -> List[T]:
    path: List[T] = [node.state]
    # work backwards from end to front
    while node.parent is not None:
        node = node.parent
        path.append(node.state)
    path.reverse()
    return path

出于显示的目的，需要用到成功路径、开始状态和目标状态来标记迷宫。删除一条路径也很有用，这样我们可以在同一个迷宫中尝试不同的搜索算法。以下两种方法应该添加文件maze.py的Maze类中。

清单20 maze.py 续

1
2
3
4
5
6
7
8
9
10
11
def mark(self, path: List[MazeLocation]):
    for maze_location in path:
        self._grid[maze_location.row][maze_location.column] = Cell.PATH
    self._grid[self.start.row][self.start.column] = Cell.START
    self._grid[self.goal.row][self.goal.column] = Cell.GOAL

def clear(self, path: List[MazeLocation]):
    for maze_location in path:
        self._grid[maze_location.row][maze_location.column] = Cell.EMPTY
    self._grid[self.start.row][self.start.column] = Cell.START
    self._grid[self.goal.row][self.goal.column] = Cell.GOAL

经过一段漫长的旅程，我们终于准备好解决这个迷宫谜题了。

清单21 maze.py 续

1
2
3
4
5
6
7
8
9
10
11
12
if __name__ == "__main__":
    # Test DFS
    m: Maze = Maze()
    print(m)
    solution1: Optional[Node[MazeLocation]] = dfs(m.start, m.goal_test, m.successors)
    if solution1 is None:
        print("No solution found using depth-first search!")
    else:
        path1: List[MazeLocation] = node_to_path(solution1)
        m.mark(path1)
        print(m)
        m.clear(path1)

一个成功的解看起来是这样的：

S****X X
 X  *****
       X*
 XX******X
  X*
  X**X
 X  *****
        *
     X  *X
        *G

星号表示我们的深度优先搜索函数从开始到目标的路径。因为每个迷宫都是随机产生的，所以不是每个迷宫都有解。

广度优先搜索

你可能会注意到，通过深度优先遍历找到的迷宫解，路径似乎不自然。它们通常不是最短路径。广度优先搜索（breadth-first search，BFS）则总是寻找最短路径，通过在搜索的每次迭代中系统地寻找远离起始状态的节点的一层。对于一些特定的问题，深度优先搜索可能比广度优先搜索更快地找到解，反之亦然。因此，在两者之间进行选择，有时是在快速找到解的可能性和找到通往目标的最短路径（如果存在的话）的确定性之间进行权衡。下图展示了一个正在进行广度优先搜索的迷宫。

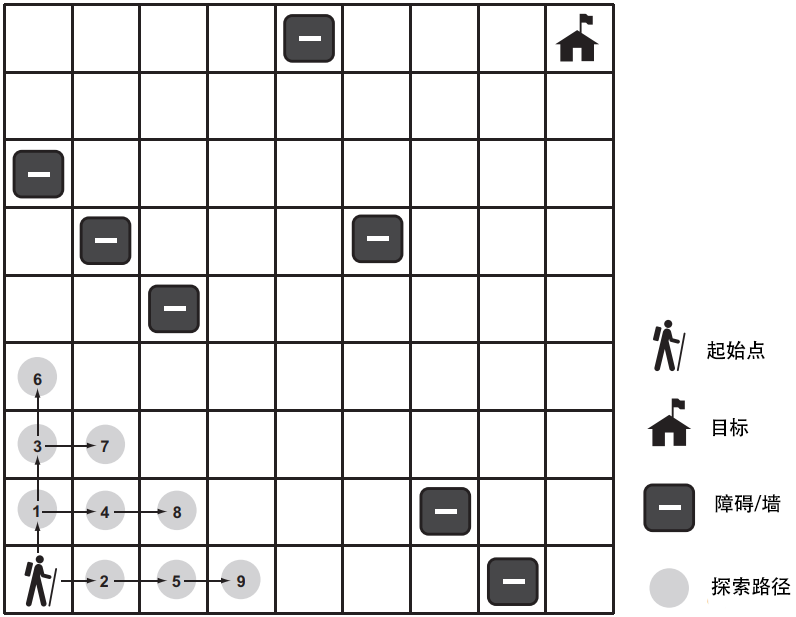
广度优先搜索

为了理解为什么深度优先搜索有时比广度优先搜索返回结果更快，想象一下在洋葱的特定层上寻找标记。使用深度优先策略的搜索者可能会将刀切入洋葱的中心，并随意检查切下的大块。如果标记层恰好在切下的大块附近，搜索者就有可能比使用广度优先策略的另一个搜索者更快地找到它，后者一次费力地剥一层洋葱。

为了更好地理解为什么广度优先搜索只要存在最短路径就总能找到，考虑寻找波士顿和纽约之间的火车停靠点最少的路径。如果一直朝同一个方向走，当遇到死胡同时就往回走（如深度优先搜索），你可能会先找到一条通往西雅图的路，然后再连接回纽约。然而，在广度优先搜索中，将首先检查离波士顿一站的所有车站。然后检查离波士顿两站的所有车站。然后检查离波士顿三站的所有车站。这将持续下去，直到找到纽约。因此，当找到纽约时，你就知道找到了最少站的路线，因为你已经检查了所有离波士顿站数较少的站，没有一个是纽约。

队列

为了实现BFS，需要一个称为队列的数据结构。堆栈是后进先出（LIFO），队列是先进先出（First-In-First-Out，FIFO）。队列就像排队上厕所。排在前面的人先去洗手间。至少，队列具有与堆栈相同的push()和pop()方法。事实上，我们的Queue实现（由Python deque支持）几乎与我们的Stack实现相同，唯一的变化是从_container的左端而不是右端移除元素，并从list切换到deque。左端的元素是仍然在队列中的最老的元素（根据到达时间），因此它们是首先弹出的元素。

清单22 generic_search.py 续

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Queue(Generic[T]):
    def __init__(self) -> None:
        self._container: Deque[T] = Deque()

    @property
    def empty(self) -> bool:
        return not self._container # not is true for empty container

    def push(self, item: T) -> None:
        self._container.append(item)

    def pop(self) -> T:
        return self._container.popleft() # FIFO

    def __repr__(self) -> str:
        return repr(self._container)

提示 为什么Queue的实现使用deque作为它的后端存储，而Stack的实现使用list作为它的后端储存？这和元素从哪弹出有关。在堆栈中，从右推进、从右弹出；在队列中，从右推进、从左弹出。Python list数据结构能从右端有效弹出，但不能从左端有效弹出。deque可以有效地从任何一端弹出。因此，在deque上有一个名为popleft()的内置方法，但在list上没有对应的方法。当然可以找到其他方法来使用列表作为队列的后端存储，但它们可能是低效的。在deque中从左弹出是一个O(1)的操作，而在list中则是一个O(n)的操作。对于列表，从左端弹出后，每个后续元素都必须向左移动一个，这使得效率低下。

BFS算法

令人惊讶的是，广度优先搜索的算法与深度优先搜索的算法相同，只不过前哨（frontier）从堆栈变成了队列。将前哨从堆栈更改为队列会更改搜索状态的顺序，并确保首先搜索最接近开始的状态。

清单23 generic_search.py 续

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def bfs(initial: T, goal_test: Callable[[T], bool], successors: Callable[[T], List[T]]) -> Optional[Node[T]]:
    # frontier is where we've yet to go
    frontier: Queue[Node[T]] = Queue()
    frontier.push(Node(initial, None))
    # explored is where we've been
    explored: Set[T] = {initial}
    
    # keep going while there is more to explore
    while not frontier.empty:
        current_node: Node[T] = frontier.pop()
        current_state: T = current_node.state
        # if we found the goal, we're done
        if goal_test(current_state):
            return current_node
        # check where we can go next and haven't explored
        for child in successors(current_state):
            if child in explored: # skip children we already explored
                continue
            explored.add(child)
            frontier.push(Node(child, current_node))
    return None # went through everything and never found goal

如果试着运行bfs()，你会发现它总能找到迷宫问题的最短解。在文件的if __name__ == "__main__ ":部分，紧接着前一个测试添加了以下测试，可以对同一迷宫比较结果。

清单24 maze.py 续

1
2
3
4
5
6
7
8
9
# Test BFS
solution2: Optional[Node[MazeLocation]] = bfs(m.start, m.goal_test, m.successors)
if solution2 is None:
    print("No solution found using breadth-first search!")
else:
    path2: List[MazeLocation] = node_to_path(solution2)
    m.mark(path2)
    print(m)
    m.clear(path2)

令人惊讶的是，你可以保持一个算法不变，只是改变它访问的数据结构，就得到完全不同的结果。下面是在之前的迷宫上调用bfs()的结果。请注意星号标记的路径从开始点到目标比前面的例子更加直接。

S    X X
*X
*      X
*XX      X
* X
* X  X
*X
*
*    X   X
*********G

A*搜索

像广度优先搜索一样，一层一层地剥洋葱会非常耗时。A*搜索和BFS一样旨在找到从起始状态到目标状态的最短路径。不同的是，A*搜索使用成本函数和启发函数的组合，集中搜索最有可能快速到达目标的路径。

成本函数g(n)检查达到特定状态的成本。就迷宫而言，则是必须经历多少步才能到达所讨论的状态。启发函数h(n)给出了从所讨论的状态到目标状态的成本估计。可以证明，如果h(n)是一个可接受的启发式（admissible heuristic）方法，那么找到的最终路径将是最优的。一个可接受的启发式方法是从不高估达到目标的成本。在二维平面上的例子是直线距离启发式，因为直线总是最短的路径。（启发式方法的更多信息，可参考Stuart Russell和Peter Norvig的Artificial Intelligence: A Modern Approach, 3rd edition (Pearson, 2010)第94页）

任何被考虑的状态的总成本是f(n)，是g(n)和h(n)的组合。也即，f(n) = g(n) + h(n)。当从前哨选择下一个要探索的状态时，A*搜索会选择f(n)最低的状态。这就是它区别于BFS和DFS的地方。

优先级队列

为了选择前哨上f(n)最低的状态，A*搜索使用优先级队列作为其前哨的数据结构。优先级队列保持其元素的内部顺序，这样弹出的第一个元素总是优先级最高的元素。（在我们的例子中，优先级最高的元素是f(n)最低的元素）通常这意味着内部使用二叉堆（binary heap），其推入操作为O(lg n)弹出操作为O(lg n)。

Python的标准库包含heappush()和heappop()函数，它们获取一个列表并将其作为二叉堆来维护。我们可以围绕这些标准库函数构建一个瘦包装器（thin wrapper），来实现优先级队列。PriorityQueue类将类似于Stack和Queue类，只不过使用heappush()和heappop()修改push()和pop()方法。

清单25 generic_search.py 续

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class PriorityQueue(Generic[T]):
    def __init__(self) -> None:
        self._container: List[T] = []

    @property
    def empty(self) -> bool:
        return not self._container # not is true for empty container

    def push(self, item: T) -> None:
        heappush(self._container, item) # in by priority

    def pop(self) -> T:
        return heappop(self._container) # out by priority

    def __repr__(self) -> str:
        return repr(self._container)

为了确定一个特定元素相对于另一个元素的优先级，heappush()和heappop()使用<运算符对它们进行比较。这就是为什么需要在Node上实现__lt__()的原因。一个Node与其他Node比较只是分别查看各自的f(n)，而f(n)只是简单地cost和heuristic属性相加。

启发式方法

启发式（heuristic）方法是对解决问题方式的直觉思考（若要了解更多关于A*寻路中的启发式方法，可参考Amit Patel的Amit’s Thoughts on Pathfinding）。对于迷宫求解，启发式方法旨在选择下一步搜索的最佳迷宫位置，以达到目标。换句话说，这是关于前哨上哪些节点更接近目标的有根据的猜测。如前所述，如果A*中的启发式方法搜索产生准确的相对结果，且该结果是可接受的，那么A*将给出最短的路径。计算较小值的启发式方法最后可能会导致搜索更多的状态，而更接近实际距离的启发式方法（但不是超过实际距离的，因为这将使它们变成不可接受的）会导致搜索更少的状态。因此，理想的启发式方法尽可能地接近实际距离，但不能超过实际距离。

欧几里得距离

正如我们在几何学中所学的，两点之间的最短路径是一条直线。因此，对于迷宫问题，直线启发式方法总是可以接受的，是合理的。从毕达哥拉斯定理导出的欧几里德距离表示distance=sqrt{(difference in x)^2 + (difference in y)^2}。对于迷宫问题，x的差异相当于迷宫两个位置之间的列的差异，y的差异相当于迷宫两个位置行的差异。请注意，我们在迷宫中实现了这一点。

清单26 maze.py 续

1
2
3
4
5
6
def euclidean_distance(goal: MazeLocation) -> Callable[[MazeLocation], float]:
    def distance(ml: MazeLocation) -> float:
        xdist: int = ml.column - goal.column
        ydist: int = ml.row - goal.row
        return sqrt((xdist * xdist) + (ydist * ydist))
    return distance

euclidean_distance()是返回函数的函数。像Python这样支持头等函数（first-class function）的语言支持这种有趣的模式。distance()捕获euclidean_distance()传递的goal MazeLocation。捕获意味着distance()可以在每次被调用时引用这个变量。它返回的函数利用目标goal进行计算。这种模式允许创建需要较少参数的函数。返回的distance()函数仅将起始迷宫位置作为参数，并永久“知道”目标。

下图显示了网格环境中的欧几里德距离，就像曼哈顿的街道一样。

欧氏距离

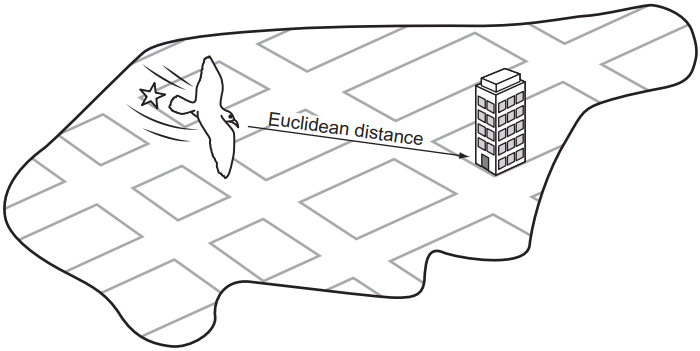
曼哈顿距离

欧几里德距离虽好，但是对于我们的特殊问题，我们可以做得更好。曼哈顿距离是通过在曼哈顿的街道上导航得出的，曼哈顿是纽约市以网格模式布局称著行政区。要从曼哈顿的某地方走到另一个地方，需要经过一定数量的水平街区和一定数量的垂直街区（曼哈顿几乎没有对角街道）。曼哈顿距离是通过简单地找出两个迷宫位置之间的行差并将其与列差相加而得出的。下图显示了曼哈顿距离。

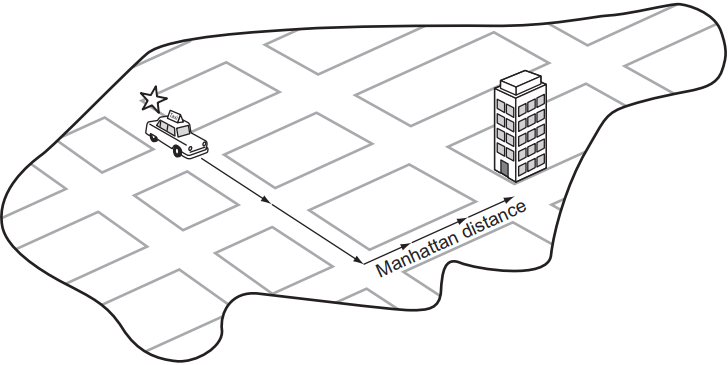
曼哈顿距离

因为这种启发式方法更准确地遵循了我们迷宫导航的现实（垂直和水平移动，而不是沿对角线移动），它比欧几里德距离更接近实际距离。因此，当一个A*搜索与曼哈顿距离相结合时，它将搜索更少的状态。解的路径仍然是最优的，因为曼哈顿距离对于只允许四个方向运动的迷宫来说是可以接受的。

A*算法

从BFS到A*搜索，我们需要做一些小的修改。首先是将前哨从队列更改为优先级队列。这样，前哨将弹出f(n)最低的节点。第二个是把探索过的集合变成字典。字典允许我们跟踪可能访问的每个节点的最低成本（g(n)）。现在使用启发式方法函数，如果启发式方法不一致，一些节点可能会被访问两次。如果通过新方向找到的节点的到达成本低于上次到达它时成本，那么接受新的路由。

为了简单起见，函数astar()不将成本计算函数作为参数。相反，我们只认为迷宫中每一跳的代价都是1。每个新Node都根据这个简单的公式分配了一个成本，并使用一个新的函数作为参数传递给搜索函数heuristic()。除了这些变化，astar()与bfs()非常相似。

清单28 generic_search.py 续

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def astar(initial: T, goal_test: Callable[[T], bool], successors: Callable[[T], List[T]], heuristic: Callable[[T], float]) ->
    Optional[Node[T]]:
    # frontier is where we've yet to go
    frontier: PriorityQueue[Node[T]] = PriorityQueue()
    frontier.push(Node(initial, None, 0.0, heuristic(initial)))
    # explored is where we've been
    explored: Dict[T, float] = {initial: 0.0}

    # keep going while there is more to explore
    while not frontier.empty:
        current_node: Node[T] = frontier.pop()
        current_state: T = current_node.state
        # if we found the goal, we're done
        if goal_test(current_state):
            return current_node
    # check where we can go next and haven't explored
    for child in successors(current_state):
        new_cost: float = current_node.cost + 1 # 1 assumes a grid, need a cost function for more sophisticated apps

        if child not in explored or explored[child] > new_cost:
            explored[child] = new_cost
            frontier.push(Node(child, current_node, new_cost, heuristic(child)))
    return None # went through everything and never found goal

恭喜你。如果你已经走了这么远，你将不仅学会如何求解迷宫问题，还学会了一些通用的搜索函数，可以在许多不同的搜索应用中使用。DFS和BFS适用于许多性能不重要的较小数据集和状态空间。在某些情况下，DFS的表现会优于BFS，但BFS的优势在于总能提供最佳路径。有趣的是，BFS和DFS有着相同的实现，只是区别在于使用队列而不是堆栈作为前哨。稍微复杂一点的A*搜索，加上一个好的、一致的、可接受的启发式搜索，不仅提供了最佳路径，而且远远超过了BFS。因为所有这三个函数都是通用实现的，所以在几乎任何搜索空间使用它们都只需一个import generic_search()。

在maze.py的测试部分用同样的迷宫测试astar()。

清单29 maze.py 续

1
2
3
4
5
6
7
8
9
# Test A*
distance: Callable[[MazeLocation], float] = manhattan_distance(m.goal)
solution3: Optional[Node[MazeLocation]] = astar(m.start, m.goal_test, m.successors, distance)
if solution3 is None:
    print("No solution found using A*!")
else:
    path3: List[MazeLocation] = node_to_path(solution3)
    m.mark(path3)
    print(m)

有趣的是，输出与bfs()略有不同，尽管bfs()和astar()都在寻找最佳路径。由于它的启发式的，astar()立即沿着对角线向目标前进。它最终将搜索比bfs()更少的状态，从而获得更好的性能。如果想自己证明这一点，加一个状态计数。

S** X X
 X**
   * X
 XX*   X
  X*
  X**X
 X ****
      *
    X * X
      **G

传教士和食人族

三个传教士和三个食人族在一条河的西岸。他们有一只能容纳两个人的独木舟，他们都必须渡到河的东岸。若两岸食人族的数量多于传教士，食人族会吃掉传教士。此外，独木舟上必须至少有一个人才能过河。什么样的渡河顺序能让整个队伍成功过河？下图说明了这个问题。

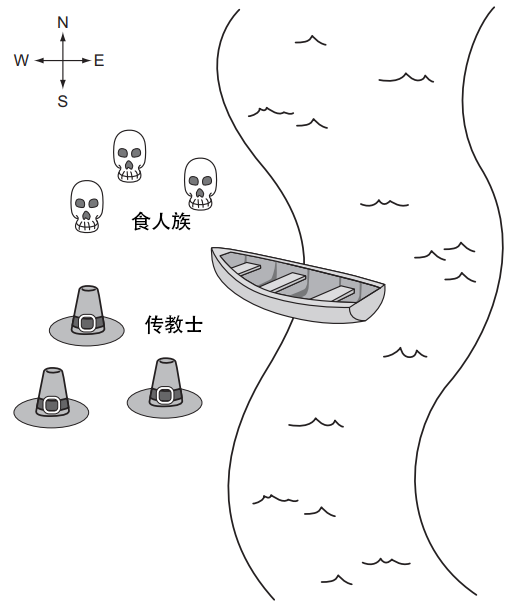
食人族与传教士

建模问题

我们将通过建立一个跟踪西岸的数据结构来解决这个问题。西岸有多少传教士和食人族？船在西岸吗？一旦有了这方面的知识，我们就能弄清楚东岸怎么样，因为任何不在西岸的东西都在东岸。

首先，我们将创建一个小的方便变量来记录传教士或食人族的最大数量。然后我们将定义主类。

清单30 missionaries.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from __future__ import annotations
from typing import List, Optional
from generic_search import bfs, Node, node_to_path

MAX_NUM: int = 3

class MCState:
    def __init__(self, missionaries: int, cannibals: int, boat: bool) -> None:
        self.wm: int = missionaries # west bank missionaries
        self.wc: int = cannibals # west bank cannibals
        self.em: int = MAX_NUM - self.wm # east bank missionaries
        self.ec: int = MAX_NUM - self.wc # east bank cannibals
        self.boat: bool = boat

    def __str__(self) -> str:
        return ("On the west bank there are {} missionaries and {} cannibals.\n"
                "On the east bank there are {} missionaries and {} cannibals.\n"
                "The boat is on the {} bank.")\
                .format(self.wm, self.wc, self.em, self.ec, ("west" if self.boat else "east"))

MCState类根据西岸传教士和食人族的数量以及船只的位置进行初始化。它还知道如何美化打印自身，这在之后展示问题的解时会很有价值。

在现有搜索函数的范围内工作，意味着我们必须定义一个函数来测试一个状态是否是目标状态，并定义一个函数来从任何状态中寻找后继者。目标测试函数，就像在迷宫求解问题中一样，非常简单。目标很简单，到达一个合适的状态，所有的传教士和食人族都在东岸。我们将它作为一种方法添加到MCState中。

清单31 missionaries.py 续

1
2
def goal_test(self) -> bool:
    return self.is_legal and self.em == MAX_NUM and self.ec == MAX_NUM

要创建后继者函数，有必要检查所有可能从一河岸到另一河岸的移动，然后检查这些移动是否是合适的状态。回想一下，合适的河岸是这样的河岸，在这，两边的食人族人数都不超过传教士。为了确定这一点，我们可以定义一个方便属性（作为MCState上的一个方法），来检查某一个状态是否合适。

清单32 missionaries.py 续

1
2
3
4
5
6
7
@property
def is_legal(self) -> bool:
    if self.wm < self.wc and self.wm > 0:
        return False
    if self.em < self.ec and self.em > 0:
        return False
    return True

为了清楚起见，实际的后继者函数有点冗长。它试图把一/两个人渡河的每一种可能的组合都加进去。一旦添加了所有可能的移动，就通过列表推导来过滤那些实际上合适的移动。这又是一个关于MCState的方法。

清单33 missionaries.py 续

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def successors(self) -> List[MCState]:
    sucs: List[MCState] = []
    if self.boat: # boat on west bank
        if self.wm > 1:
            sucs.append(MCState(self.wm - 2, self.wc, not self.boat))
        if self.wm > 0:
            sucs.append(MCState(self.wm - 1, self.wc, not self.boat))
        if self.wc > 1:
            sucs.append(MCState(self.wm, self.wc - 2, not self.boat))
        if self.wc > 0:
            sucs.append(MCState(self.wm, self.wc - 1, not self.boat))
        if (self.wc > 0) and (self.wm > 0):
            sucs.append(MCState(self.wm - 1, self.wc - 1, not self.boat))
    else: # boat on east bank
        if self.em > 1:
            sucs.append(MCState(self.wm + 2, self.wc, not self.boat))
        if self.em > 0:
            sucs.append(MCState(self.wm + 1, self.wc, not self.boat))
        if self.ec > 1:
            sucs.append(MCState(self.wm, self.wc + 2, not self.boat))
        if self.ec > 0:
            sucs.append(MCState(self.wm, self.wc + 1, not self.boat))
        if (self.ec > 0) and (self.em > 0):
            sucs.append(MCState(self.wm + 1, self.wc + 1, not self.boat))
    return [x for x in sucs if x.is_legal]

求解问题

我们现在有了解决问题的所有要素。回想一下，当我们使用搜索函数bfs()、dfs()和astar()来解决一个问题时，我们得到了一个Node，最终使用node_to_path()将它转换成一个状态列表，从而得到一个解。我们仍然需要的是一种方法，将这份清单转化为一系列可理解的打印步骤，以解决传教士和食人族的问题。

函数display_solution()将解路径转换为打印输出，这是一个人类可读的（human-readable）解。工作原理是，通过遍历解路径中的所有状态，同时跟踪最后一个状态。它着眼于最后一个状态和它目前正在迭代的状态之间的差异，以找出有多少传教士和食人族渡河，向哪个河岸移动。

清单34 missionaries.py 续

1
2
3
4
5
6
7
8
9
10
11
12
def display_solution(path: List[MCState]):
    if len(path) == 0: # sanity check
        return
    old_state: MCState = path[0]
        print(old_state)
    for current_state in path[1:]:
        if current_state.boat:
            print("{} missionaries and {} cannibals moved from the east bank to the west bank.\n".format(old_state.em - current_state.em, old_state.ec - current_state.ec))
        else:
            print("{} missionaries and {} cannibals moved from the west bank to the east bank.\n".format(old_state.wm - current_state.wm, old_state.wc - current_state.wc))
        print(current_state)
        old_state = current_state

display_solution()函数利用了这样一个事实，即MCState知道如何通过__str__()美化打印自己的摘要。

我们需要做的最后一件事实际上是解决传教士和食人族的问题。为了做到这一点，可以重用已经实现的搜索函数，因为我们实现的是一个通用版本。这次我们使用bfs()（因为使用dfs()需要用相同的值将引用的不同状态标记为相等，而astar()需要一种启发式方法）。

**

1
2
3
4
5
6
7
8
if __name__ == "__main__":
    start: MCState = MCState(MAX_NUM, MAX_NUM, True)
    solution: Optional[Node[MCState]] = bfs(start, MCState.goal_test, MCState.successors)
    if solution is None:
        print("No solution found!")
    else:
        path: List[MCState] = node_to_path(solution)
        display_solution(path)

可以看到我们实现的通用搜索函数很灵活。它们可以很容易地适用于解决各种各样的问题。你应该会看到如下输出（节略）：

On the west bank there are 3 missionaries and 3 cannibals.
On the east bank there are 0 missionaries and 0 cannibals.
The boast is on the west bank.
0 missionaries and 2 cannibals moved from the west bank to the east bank.
On the west bank there are 3 missionaries and 1 cannibals.
On the east bank there are 0 missionaries and 2 cannibals.
The boast is on the east bank.
0 missionaries and 1 cannibals moved from the east bank to the west bank.
…
On the west bank there are 0 missionaries and 0 cannibals.
On the east bank there are 3 missionaries and 3 cannibals.
The boast is on the east bank.

实际应用

搜索在所有有用的软件中都起着一定的作用。在某些情况下，它是核心元素（Google 搜索、Spotlight、Lucene）；在其他情况下，它是使用数据存储结构的基础。了解应用于数据结构的正确搜索算法对性能至关重要。例如，在已排序的数据结构上使用线性搜索而不用二分搜索会产生非常昂贵的性能代价。

A*是应用最广泛的寻路算法之一。只有在搜索空间做预先计算的算法才能打败它。对于盲目搜索（blind search）来说，A*还没有在所有场景中被可靠地击败，这使得它成为从路径规划到找出最短路径的重要组成部分。大多数提供方位的地图软件（如谷歌地图）使用Dijkstra算法（A*是其变体）来导航。每当游戏中的人工智能角色在没有人工干预的情况下寻找从一端到另一端的最短路径时，它可能会使用A*。

广度优先搜索和深度优先搜索通常是更复杂的搜索算法的基础，如一致代价搜索（uniform-cost search）和回溯搜索（backtracking search）。广度优先搜索通常是在相当小的图中找到最短路径的一种够用的技术。但是由于它与A*的相似性，如果对于一个更大的图存在一个好的启发式方法，那么很容易用A*来替代。

练习

  1. 创建一个包含一百万个数字的列表，对本章中定义的linear_contains()和binary_contains()函数查找列表中的各种数字所需的时间进行计时，显示二分搜索相对于线性搜索的性能优势。
  2. 在dfs()、bfs()和astar()中添加一个计数器，查看每种搜索方法对于相同迷宫中搜索了多少个状态。找出100个不同迷宫的计数，获得统计上有意义的结果。
  3. 为不同数量的初始传教士和食人族找到解决传教士和食人族问题的方法。提示：可能需要向MCState添加__eq__()和__hash__()方法的重写。

翻译自：Classic Computer Science Problems in Python，第2章Search problems。