机器学习中的一阶与随机优化方法:机器学习模型
在本章中,我们介绍了一些广泛使用的统计和机器学习模型,以激发后面对优化理论和算法的讨论。
线性回归
让我们从一个简单的例子开始。朱莉需要决定是否去“竹园”餐厅吃午饭,她找到去过这家餐馆的朋友朱迪和吉姆,他们两人对这家餐馆的服务都给了3分(1到5分)。鉴于这些评分,朱莉很难决定是否应该去“竹园”。幸运的是,她保留了一张朋友们和她自己对一些其他餐馆的评分表,如表1.1所示。
| 餐馆 | 朱迪的评分 | 吉姆的评分 | 朱莉的评分 |
|---|---|---|---|
| Goodfellas | 1 | 5 | 2.5 |
| Hakkasan | 4.5 | 4 | 5 |
| … | … | … | … |
| 竹园 | 3 | 3 | ? |
我们用$u^{(i)}$来表示“输入”变量(在本例中是朱迪和吉姆的评分),输入变量也被称为输入特征,$v^{(i)}$表示预测的“输出”或目标变量(在本例中是朱莉的评分)。一对$(u^{(i)}, v^{(i)})$被称为训练样本,而一组$N$对训练样本${(u^{(i)}, v^{(i)}), \quad, i = 1, \dots, N}$被称为训练集。我们用$U$来表示输入值的空间,用$V$表示输出值的空间。在本例中,$U=\Bbb R^2$、$V=\Bbb R$。特别地,$u_1^{(1)}$和$u_2^{(1)}$分别表示朱迪和吉姆对Goodfellas的评分,而$v^{(1)}$表示朱莉对Goodfellas的评分。
我们的目标是,给定一个训练集,学习一个函数$h: U \to V$,使得$h(u)$是$v$相应值的一个“好”预测器。函数$h$通常被称为假设或决策函数。上述类型的机器学习任务被称为监督学习(supervised learning)。当输出$v$是连续的,称学习任务为回归。另外,如果$v$是离散的,则称学习任务为分类。回归和分类是监督学习的两个主要任务。
近似$v$的一个简单想法是通过$u$的线性函数:
$$h(u) = h_0(u) = \theta_0 + \theta_1 u_1 + \dots + \theta_n u_n$$
在上面的例子中,n为2。为了便于标记,引入$u_0=1$的约定,因此我们有
$$h(u) = \sum_{i=0}^n\theta_i u_i = \theta^T u$$
其中,$\theta = (\theta_0;\dots;\theta_n)$、$u=(u_0;\dots;u_n)$。为了找出参数$\theta \in \Bbb R^{n + 1}$,我们构建如下优化问题
$$\underset{\theta}{min} \Bigl { f(\theta) := \sum_{i=1}^N\bigl ( h_\theta (u^{(i)}) - v ^ {(i)}\bigr )^ 2 \Bigr } \tag{1.1.1}$$
这产生了普通最小二乘(ordinary least square)回归模型。
为推导式(1.1.1)中$\theta$的解,令
$$U = \begin{bmatrix}{u^{(1)}}^T \ {u^{(2)}}^T \ \vdots \ {u^{(N)}}^T\end{bmatrix}$$
U有时被称为设计矩阵,它由所有的输入变量组成。
那么,$f(\theta)$可以写成:
$$\begin{aligned} f(\theta) & = \sum_{i=1}^N({u^{(i)}}^T \theta - v^{(i)})^2 \
& = (U \theta - v)^T (U \theta - v) \
& = \theta^T U^T U \theta - 2 \theta^T U^T v - v^T v \end{aligned}
$$
取$f(\theta)$的导数为零,我们得到了正规方程
$$U^T U \theta - U^T v = 0$$
式(1.1.1)的最小值由下式给出
$$\theta^{ * } = (U^T U) ^{-1} U^T v$$
普通最小二乘回归是极少数有明确解的机器学习模型之一。但是请注意要计算$\theta^{ * }$,需要计算$(n + 1) \times (n + 1)$矩阵$U^T U$的逆。如果n的维度很大,其逆矩阵的计算代价仍然很昂贵。
式(1.1.1)优化问题的公式遵循一种相当直观的方法。接下来,我们提供了一些关于这个公式的统计推理。令
$$\epsilon^{(i)} = v^{(i)} - \theta^Tu^{(i)}, \quad i = 1, \dots, N \tag{1.1.2}$$
换句话说,$\epsilon^{(i)}$表示用$\theta^Tu^{(i)}$逼近$v^{(i)}$误差。此外,假设$\epsilon^{(i)}, \quad i = 1, \dots, N$,独立同分布(i.i.d.),且服从均值为0,方差为$\sigma^2$的高斯(正态)分布。$\epsilon^{(i)}$的密度由下式给出
$$p(\epsilon^{(i)}) = \frac{1}{\sqrt{2\pi}\sigma} \text{exp} (-\frac{(\epsilon^{(i)})^2}{2\sigma^2})$$
将(1.1.2)代入上式,我们有
$$p(v^{(i)}|u^{(i)}; \theta) = \frac{1}{\sqrt{2\pi}\sigma} \text{exp} \bigl ( - \frac{(v^{(i)} - \theta^T u^{(i)})^2}{2 \sigma^2} \bigr ) \tag{1.1.3}$$
这里,$p(v^{(i)}|u^{(i)}; \theta)$表示给定输入$u^{(i)}$并由$\theta$参数化的输出$v^{(i)}$的分布。
给定输入变量$u^{(i)}$和输出变量$v^{(i)}$,$i = 1, \dots, N$,关于(with respect to,w.r.t)参数$\theta$的似然函数定义为
$$L(\theta) := \prod_{i = 1}^N p(v^{(i)} | u^{(i)};\theta) = \prod_{i=1}^N \frac{1}{\sqrt{2\pi}\sigma} \text{exp}(- \frac{(v^{(i)} - \theta^T u^{(i)})^2}{2\sigma^2})$$
最大似然( maximum likelihood)原理告诉我们,我们应该选择$\theta$来最大化似然$L(\theta)$,或者等价地,对数似然(log likelihood)
$$\begin{aligned} l(\theta) &:= \text{log} L(\theta) \
& = \sum_{i = 1}^N log \Bigl [ \frac{1}{\sqrt{2\pi}\sigma} \text{exp} \bigr ( - \frac{(v^{(i)} - \theta^T u^{(i)})^2}{2 \sigma^2}\bigl ) \Bigr ] \
& = N log \frac{1}{\sqrt{2 \pi} \sigma} - \frac{1}{2\sigma^2} \sum_{i = 1}^N (v^{(i)} - \theta^T u^{(i)})^2
\end{aligned}$$
这正是普通最小二乘回归问题,即关于$\theta$最小化$\sum_{i = 1}^N(v^{(i)} - \theta^T u^{(i)})^2$。上述推理告诉我们,在某些概率假设下,普通最小二乘回归与最大似然估计是一样的。然而,应该注意的是,概率假设绝不是最小二乘法回归的合理过程所必需的。
逻辑回归
让我们回到前面的例子。假设朱莉只关心她是否喜欢“竹园”餐厅,而不关心具体评分。此外,她只记录了喜欢或不喜欢某些餐馆的历史数据,如表1.2所示。这些记录也展示在图1.1中,其中每个餐馆由绿色的“O”或红色的“X”表示,分别她喜欢或不喜欢该餐馆。问题是:她的两个朋友都给了“竹园”餐厅3分,那么她会喜欢“竹园”吗?她能利用过去的数据做出合理的决策吗?
| 餐馆 | 朱迪的评分 | 吉姆的评分 | 朱莉喜欢? |
|---|---|---|---|
| Goodfellas | 1 | 5 | 否 |
| Hakkasan | 4.5 | 4 | 是 |
| … | … | … | … |
| 竹园 | 3 | 3 | ? |
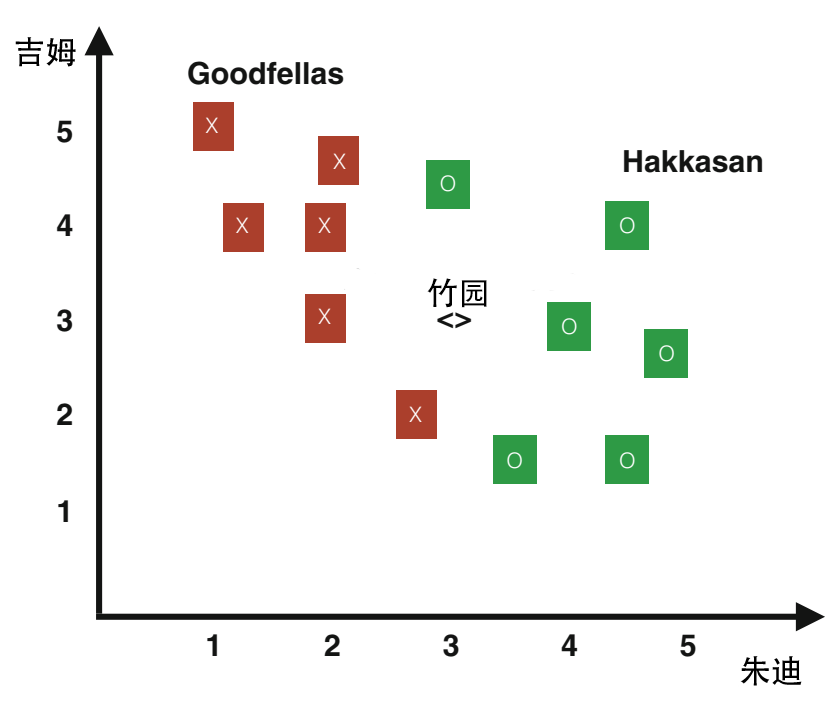
类似于回归模型,输入值仍然表示为$U = ({u^{(1)}}^T;\cdots;{u^{(N)}}^T)$,也即,朱迪和吉姆给出的评分。但是现在的输出值是二值化的,即$v^{(i)} \in {0, 1}, \quad i = 1, \dots, N$,这里$v^{(i)} = 1$表示朱莉喜欢第i家餐馆,$v^{(i)} = 0$表示她不喜欢这家餐馆。朱莉的目标是想出一个决策函数$h(u)$来近似这些二值化变量。这种类型的机器学习任务被称为二元分类(binary classification)。
朱莉的决策函数可以简单的是她朋友评分的加权线性组合:
$$h_{\theta}(u) = \theta_0 + \theta_1 u_1 + \dots + \theta_n u_n \tag{1.2.1}$$
其中,n = 2。(1.2.1)中决策函数的一个明显问题是,它的值可以任意大小。另一方面,它值落在0和1之间,因为值代表v的范围。使h落在0和1之间的一个简单方法是通过sigmoid函数(logistic函数)来映射线性决策函数$\theta^T u$
$$g(z) = \frac{1}{1 + \text{exp}(-z)} \tag{1.2.2}$$
且定义决策函数为
$$h_{\theta}(u) = g(\theta^T u) = \frac{1}{1 + \text{exp} (- \theta^T u)} \tag{1.2.3}$$
注意sigmoid函数的取值范围是(0, 1),如图1.2所示。
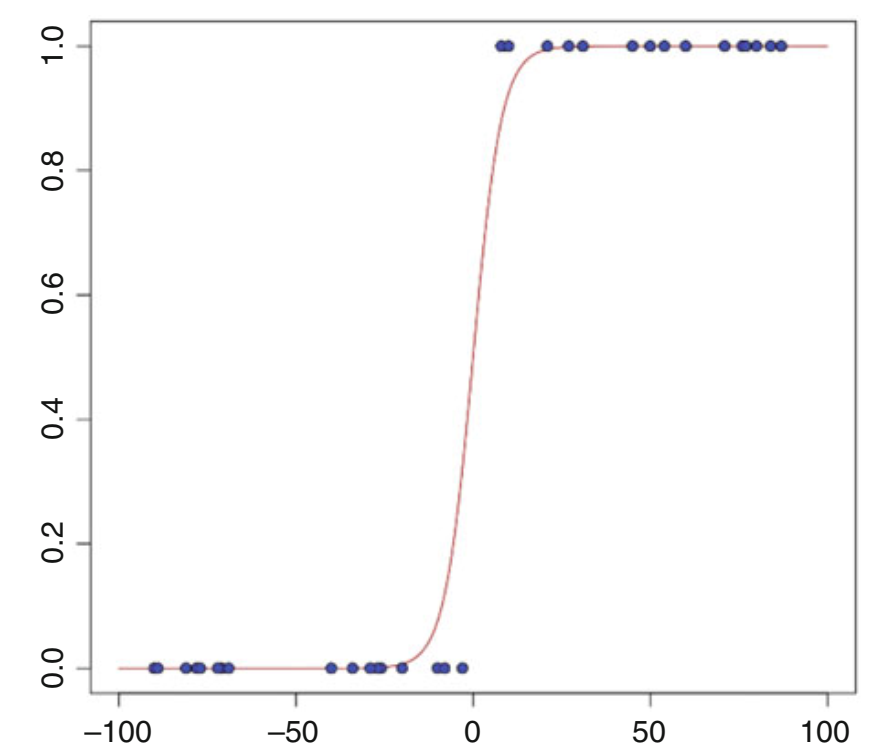
现在的问题是如何确定(1.2.3)中决策函数的参数$\theta$。我们已经看到,普通最小二乘回归模型的推导,是在某些概率假设下,最大似然估计的结果。对于分类问题,我们将遵循类似的方法。
我们假设$v^{(i)}, \quad i = 1. \dots, N$是独立伯努利随机变量,其成功概率(或平均值)为$h_\theta(u^{(i)})$。因此,它们的概率质量函数由下式给出
$$p(v^{(i)} | u^{(i)}; \theta) = [h_\theta(u^{(i)})]^{v{(i)}} [1 - h_\theta(u^{(i)})]^{1 - v^{(i)}}, \quad v ^ {(i)} \in {0, 1}$$
相应的似然函数$L(\theta)$定义为
$$L(\theta) = \prod_{i=1}^N \bigl { [h_\theta(u^{(i)})]^{v{(i)}} [1 - h_\theta(u^{(i)})]^{1 - v^{(i)}} \bigr }$$
鉴于最大似然原理,我们打算最大化$L(\theta)$,或等效地,最大化对数似然
$$\begin{aligned} l(\theta) &= \sum_{i = 1}^N \text{log} \Bigl { \bigl [ h_\theta(u^{(i)})\bigr ]^{v^{(i)}} \bigl [ 1 - h_\theta(u^{(i)}) \bigr]^{1 - v^{(i)}} \Bigl } \
&= \sum_{i = 1}^N \Bigl { v^{(i)} \text{log} h_\theta (u^{(i)}) + \bigl [1 - v^{(i)} \bigr ] \text{log} \bigl [ 1 - h_\theta (u^{(i)}) \bigr ] \Bigr }
\end{aligned}$$
相应地,我们构造最优化问题
$$\underset{\theta}{\text{max}} \sum_{i = 1}^N \Bigl { - \text{log} \bigl [ 1 + \text{exp} (-\theta^T u ^{(i)}) \bigr ] - \bigl [ 1 - v^{(i)}\bigr ] \theta^T u^{(i)} \Bigr } \tag{1.2.4}$$
尽管该模型用于二分类,但由于历史原因,它通常被称为逻辑回归。
与线性回归不同,(1.2.4)没有明确的解。我们需要开发一些数值程序来找到它的近似解。这些程序被称为优化算法,将在以后的讲义中深入研究。
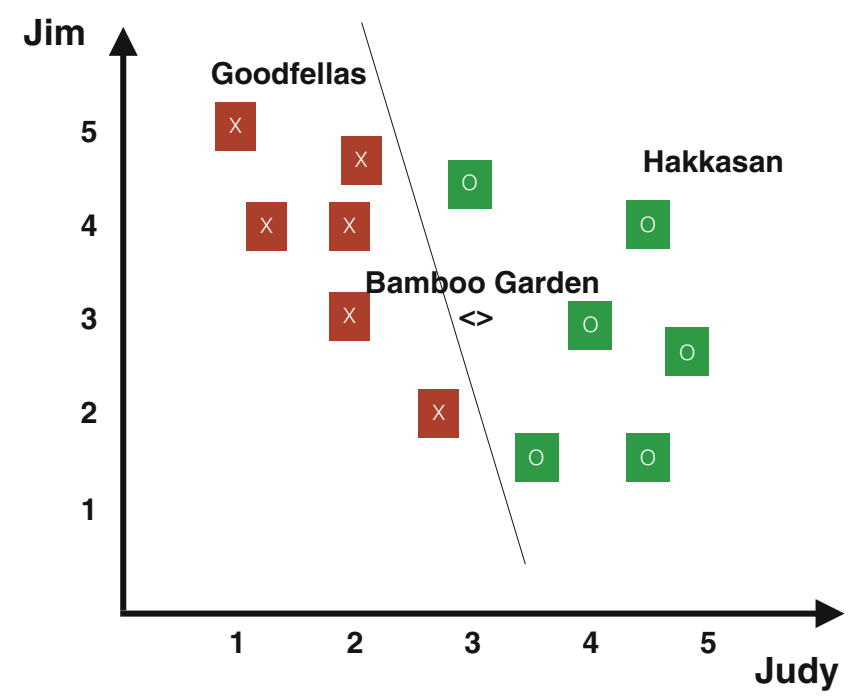
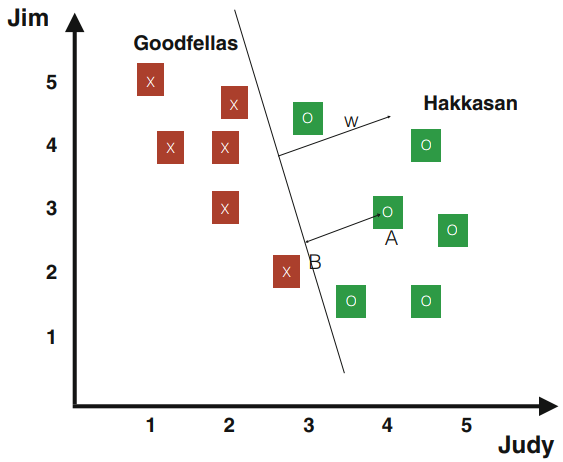
假设朱莉可以求解上述问题,并找到至少一个最优解$\theta^{ * }$。她将得到了一个决策函数$h_{\theta^{ * }} (u)$,该函数可以用来预测她是否喜欢一家新餐馆(如“竹园”)。更具体地,回想一下“竹园”对应的样本是$u = (1, 3, 3)$ (注意$u_0 = 1$)。如果$h_{\theta^{ * }} ((1, 3, 3)) > 0.5$,那么认为朱莉会喜欢这家餐馆,否则不会。使$h_{\theta^{ * }}(u)$为0.5的u值称为“决策边界”,如图1.3所示。黑线是“决策边界”。位于决策边界之上的点代表朱莉喜欢的餐馆,而位于决策边界之下的点代表她不喜欢的餐馆。对于该决定界限,竹园在上边,这意味着朱莉可能会喜欢这家餐馆。
广义线性模型
在前两节中,我们介绍了两种有监督机器学习模型:普通最小二乘回归和逻辑回归。对于前一个模型,我们假设$v|u;\theta \sim \mathcal{N} (\mu,\sigma^{2})$;对于后一种模型,假设$v|u; \theta \sim \text{Bernoulli} (q)$,是对$\mu$和$q$作为$u$和$\theta$的函数的一些适当定义。在本节中,我们将说明这两种模型都是广义线性模型(Generalized Linear Models,GLMs)的一种特殊情况,它本质上是对指数分布族应用最大似然估计。
指数分布族
指数分布族是指,对于固定的T、a和b,以下列形式给出的一组概率分布
$$p(v;\eta) = b(v) \text{exp} (\eta^T T(v) - a(\eta)) \tag{1.3.1}$$
该族由$\eta$参数化,即通过改变$\eta$可以得到不同的分布
让我们首先检查一下正态分布确实可以写成(1.3.1)的形式。为简单起见,我们考虑随机变量$v \sim \mathcal{N}(\mu, 1)$,即,
$$\begin{aligned}
p(v; \mu) &= \frac{1}{\sqrt{2\pi}} \text{exp} (- \frac{(v - \mu)^2}{2}) \
&= \frac{1}{\sqrt{2 \pi}} \text{exp} (-\frac{v^2}{2}) \text{exp} (\mu^T v - \frac{\mu^2}{2})
\end{aligned}$$
显然,$p(v; \mu)$是$\eta = \mu$的特殊情况。
$$b(v) = \frac{1}{\sqrt{2 \pi}}\text{exp} (- \frac{v^2}{2}), \quad T(v) = v \text{且} a(\eta) = \frac{\mu^2}{2} = \frac{\eta^2}{2}$$
为了验证伯努利分布是一种特殊的指数分布,我们首先重写它的密度函数
$$
\begin{aligned} p(v; q) &= q^v (1 - q)^{1 - v} \
&= \text{exp} \bigl (v \text{log} q + (1 - v) \text{log} (1 - q) \bigr ) \
&= \text{exp} \bigl (v \text{log} \frac{q}{1 - q} + \text{log} (1 - q) \bigr )
\end{aligned}$$
显然,鉴于(1.3.1),我们有
$$\eta = \text{log} \frac{q}{1 - q}, b(v) = 1, T(v) = v \text{且} a(\eta) = - \text{log} (1 - q)$$
有趣的是,通过第一项,我们有
$$q = \frac{1}{1 + \text{exp} (- \eta)}$$
这就是sigmoid函数。
指数分布族涵盖了一大类分布,包括正态(normal)、指数(exponential)、伽玛(gamma)、卡方(chi-squared)、贝塔(beta)、狄利克雷(Dirichlet)、伯努利(Bernoulli)、分类(categories)、泊松(Poission)、威沙特(Wishart)和逆威沙特(Inverse Wishart)分布等。
模型构建
根据我们如何构建普通最小二乘法和逻辑回归模型的过程,我们可以将GLM模型的基本要素总结如下。
给定输入$u$和待估计的参数$\theta$,我们需要知道响应(输出)$v$的分布。更具体地,我们假设$v|u;\theta$满足一族由$\eta$参数化的指数分布。
给定$u$,我们需要构造一个决策函数(或假设)$h(u)$来预测结果$T(v)$(在大多数情况下,$T(v) = v$,就像普通最小二乘法和逻辑回归一样)。$T(v)$是随机的,我们期望$h(u) = \Bbb{E}[T(v)|u]$。例如,在逻辑回归中,我们选择$h$的方式是$h_\theta (u) = \Bbb{E} [v|u]$。
我们假设$\eta$线性依赖于输入值$u$,即$\eta = \theta^T u$。如果$\eta$是一个向量,我们假设$\eta_i = \theta_i^T u$。
前两个要素是我们做出的假设,最后一个要素与模型的设计更相关。有了这种类型的设计,最终的模型很可能更容易拟合。
让我们检查一下这些要素在普通最小二乘模型的开发中是否被使用过。回想一下,我们假设$\epsilon = v - \theta^T u$是服从$\mathcal{N}(0, \sigma^2)$的正态分布。因此,$v|u;\theta \sim \mathcal{N}(0, \sigma^2), \quad \eta = \theta^T u$。这意味着上述三个要素都成立,因为$v|u; \theta$为正态分布,$\eta = \Bbb{E} [v|u; \theta]$且$h(u) = \theta^T, u = \eta$。
接下来,我们可以检查这些元素是否也适用于逻辑回归。回想一下,我们假设$v|u;\theta$满足一族伯努利分布,其均值为
$$q = h(u) = \frac{1}{1 + \text{exp} (- \theta^T u)}$$
记$\eta = \theta^T u$,并在上述等式中使用它,我们得到
$$q = \frac{1}{1 + \text{exp} ( - \eta)}$$
或,等价地,
$$\eta = \text{log} \frac{q}{1 - q}$$
这正是我们用来以指数族形式写出伯努利分布的参数。这些讨论意味着GLM的所有上述要素都成立。
让我们再看一个GLM的例子。考虑一个分类问题,其中响应变量$v$可以取$k$个值中的任何一个,即$v \in {1, 2, \dots, k}$。响应变量仍然是离散的,但是现在可以取两个以上的值。这种机器学习任务被称为多分类。
为了推导用于建模这种类型任务的GLM,我们首先假设$v$服从多项式分布,并且指出多项式分布是指数族分布。
为了对$k$个可能结果的多项式进行参数化,我们可以使用$k$个参数$q_1, \dots, q_k$来指定每个结果的概率。然而,这些参数不是独立的,由于$\sum_{i = 1}^k = q_i = 1$,任何$k - 1$ 个 $q_i$唯一地确定最后一个。因此,我们将改为用$k - 1$个参数,$q_1, \dots, q_{k - 1}$(其中,$q_i = p(y = i; q)$),参数化多项式。为了便于标注,令$q_k = p(y = k; q) = 1 - \sum_{i = 1}^{k - 1}q_i$。
为了证明多项式分布是指数分布,我们将$T(v) \in \Bbb{R}^{k - 1}$定义如下:
$$T(1) = \begin{bmatrix} 1 \ 0 \ 0 \ \vdots \ 0\end{bmatrix},
T(2) = \begin{bmatrix} 0 \ 1 \ 0 \ \vdots \ 0\end{bmatrix},
\cdots,
T(k - 1) = \begin{bmatrix} 0 \ 0 \ 0 \ \vdots \ k - 1\end{bmatrix},
T(k) = \begin{bmatrix} 0 \ 0 \ 0 \ \vdots \ 0\end{bmatrix}
$$
与前面的例子不同,这里没有$T(v) = v$,而且$T(v) \in \Bbb{R}^{k - 1}$,而不是实数。我们用$\bigl ( T(v) \bigr )_ i$来表示向量$T(v)$的第i个元素。
我们引入一个更有用的符号。如果参数为真,指示函数$I\{\cdot\}$的值为1,否则为0。因此,我们也可以把$T(v)$和$v$之间的关系写成$\bigl ( T(v) \bigl )_ i = I\{ v = i \}$。此外,我们还有$\Bbb{E} \Bigl [ \bigl ( T(v) \bigr )_ i \Bigr ] = p(v = i) = q_i$。
我们现在准备证明多项式分布是指数族的一员。我们有:
$$
\begin{aligned}
p(v; q) &= q_1^{I{v = 1}} q_2^{I{v = 2}} \dots q_k^{I{v = k}} \
&= q_1^{I{v = 1}} q_2^{I{v = 2}} \dots q_k^{1 - \sum_{i=1}^{k-1}I{v = i}} \
&= q_1^{\bigl (T(v) \bigr)_ 1} q_2^{\bigl (T(v) \bigr)_ 2} \dots q_k^{1 - \sum_{i = 1}^{k - 1} \bigl (T(v) \bigr)_ i} \
&= \text{exp} \Bigl ( \sum_{i = 1}^{k - 1} \bigl ( T(v) \bigr)_ i \text{log} q_i + (1 - \sum_{i = 1}^{k - 1} \bigl ( T(v) \bigr )_ i ) \text{log} q_k \Bigr ) \
&= \text{exp} \bigl ( \sum_{i = 1}^{k - 1} (T(v))_ i \text{log} \frac{q_i}{q_k} + \text{log} q_k \bigr)
\end{aligned}
$$
这是一个指数分布
$\eta_i = \text{log} \frac{q_i}{q_k}, i = 1, \dots, k - 1, a(\eta) = -\text{log} q_k, \text{且} b = 1 \tag{1.3.2}$
为了定义决策函数,我们首先用$\eta_i$表示$q_i$,因为$\Bbb{E} \Bigl [ \bigl ( T(v) \bigr )_ i \Bigr ] = p(v = i) = q_i$,我们希望$h_i(u) = q_i$。通过(1.3.2),我们有
$$\frac{q_i}{q_k} = \text{exp} (\eta_i), \quad i = 1, \dots, k - 1 \tag{1.3.3}$$
为了方便起见,让我们记$\eta_k = 0$,
$$\frac{q_k}{q_k} = \text{exp}(\eta_k)$$
依据上述等式,并利用$\sum_{i = 1}^k q_i = 1$,我们得到$\frac{1}{q_k} = \sum_{i = 1}^k \text{exp} (\eta_i)$,因此
$$q_i = \frac{\text{exp} \eta_i}{\sum_{i = 1}^k \text{exp} (\eta_i)}, \quad i = 1, \dots, k - 1 \tag{1.3.4}$$
为了完成决策函数的定义,我们假设$h_i(u) = q_i$,并且设置$\eta_i = \theta_i^T u$。将这两个关系与(1.3.4)一起使用,我们得到
$$h_i(u) = \frac{\text{exp} (\theta^T u)}{\sum_{i=1}^k \text{exp} (\theta_i^T u)}, \quad i = 1, \dots, k - 1$$
最后,这些在$h_i(u)$中使用的参数$\theta_i, i = 1, \dots, k - 1$。可以通过最大化对数似然来估计
$$l(\theta) = \sum_{i = 1}^N \text{log} p(v^{(i)}|u^{(i)};\theta) = \sum_{i = 1}^{N} \text{log} \prod_{j=1}^k\bigl ( \frac{\text{exp} (\eta_j)}{\sum_{j=1}^k \text{exp} (\eta_j)} \bigr )^{I{v^{(i)} = j}}$$
支持向量机
在这一节中,我们将简要介绍支持向量机(support vector machine,SVM),它是最成功的分类模型之一。
考虑具有$N$个训练样本$(u^{(i)}, v^{(i)}), \quad i = 1, \dots N$。为方便起见,我们在本节中假设输出$v^{(i)}$由1或-1给出,即$v^{(i)} \in { -1, 1}$,而不是前面章节中的$v^{(i)} \in {0, 1}$。请注意,这只是该类标签的更改,并不影响某个特定样本属于某类的事实。
目前我们假设这些观察到的样本是可分离的。从形式上讲,我们假设存在一个$u$的线性函数,表示为
$$h_{w, b} (u) = b + w_1 u_1 + w_2 u_2 + \dots + w_n u_n$$
使得,对于所有$i = 1, \dots, N$,
$$h_{w, b} (u^{(i)})
\begin{cases}
0, & \text{若 $v^{(i)} = 1$} \
< 0, & \text{其他(即,$v^{(i)} = -1$)}
\end{cases}$$
特别是,$h_{w, b} (u) = 0$定义了一个超平面,它将观察到的样本分成两个不同的类。落入超平面上方的样本用$v^{(i)} = 1$标记,而落入超平面下方的样本用$v^{(i)} = -1$标记。请注意,我们这里的决策函数$h_{w, b}$的符号也与前面的部分略有不同。首先,我们去掉了假设为1的$u_0$。其次,我们不同的符号分别表示法向量$w := (w_1, \dots, w_n)$和截距$b$,而不是单一的n + 1个向量$(\theta_0, \theta_1, \dots, \theta_n)$。主要原因是我们将研究分离超平面$h_{w, b} (u) = 0$的法向量$w$的几何意义。
通过逻辑回归,我们可以定义一个分离超平面。回想一下,我们使用决策函数$h_\theta(u) = g(\theta^Tu)$来近似概率$p(y = 1|x; \theta)$。给定一个$u$,我们根据$h_\theta(u) \ge 0.5$或$h_\theta(u) \lt 0.5$,或等价地,$\theta^T u \ge 0$或$\theta^Tu \lt 0$,预测其输出为1或0。因此,这个向量$\theta$产生了一个可能的分离超平面,如图1.4中的H1所示。
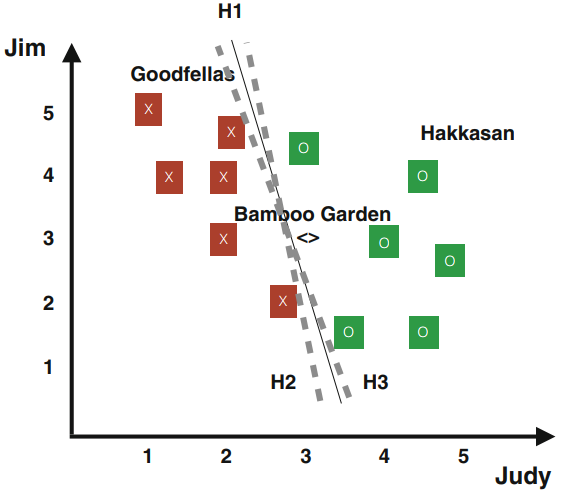
然而,有相当多的其他超平面可以分隔这些观察到的样本,例如H2和H3,如图1.4所示。
给定潜在的无限个分离超平面,我们应该如何评估它们,从而选择最适合的分离超平面?
为了回答这个问题,让我们来研究与分离超平面$w^Tu + b = 0$相关的所谓“裕度”(margin)。对于给定的样本$u^{(i)}$,即在图1.5中的点$A=(u_1^{(i)}, \dots, u_n^{(i)})$,我们首先计算它到分离超平面的距离。假设B是A到分离超平面的投影,那么足以计算线段$\overrightarrow{BA}$的长度,这里用$d^{(i)} = |\overrightarrow{BA}|$表示。注意,$\overrightarrow{BA}$的单位方向由$w/|w|$给出,因此B的坐标由$u^{(i)} - d^{(i)} w / | w|$给出。同时,由于B属于分离超平面,我们有
$$w^T \bigl( u^{(i)} - d^{(i)} \frac{w}{| w |}\bigr) + b = 0$$
求解上述关于$d^{(i)}$的方程,我们有
$$d^{(i)} = \frac{w^T u^{(i)} + b}{| w |} \tag{1.4.1}$$
在上述推导中,我们隐含地假设点A位于分离超平面之上(即$v^{(i)} = 1$)。如果点A位于超平面($v^{(i)} = -1$)之下,那么点B应该写成$u^{(i)} +d^{(i)} w/| w |$,因此
$$d^{(i)} = -\frac{w^T u^{(i)} + b}{| w |} \tag{1.4.2}$$
将(1.4.1)和(1.4.2)放在一起,对于任意的$i = 1, \dots, N$,我们可以用下列公式表示距离$d^{(i)}$
$$d^{(i)} = \frac{v^{(i)} [w^T u^{(i)} + b]}{| w |} \tag{1.4.3}$$
通过以上对$d^{(i)}$的计算,我们现在可以定义与分离超平面$w^Tu + b$相关的裕度,通过
$$d(w, b) := \underset{i=1,\dots, N}{\text{min}} d^{(i)} \equiv \frac{\underset{i=1, \dots, N}{\text{min}} v^{(i)} [w^T u^{(i)} + b]}{| w |} \tag{1.4.4}$$
裕度$d(w,b)$提供了一种评估分离超平面强度的方法。直观地说,较大的裕度意味着分离超平面可以更显著地区分两类不同的样本。
因此,一个合理的目标是找到$(w, b)$使裕度$d(w, b)$最大化,即,
$$\underset{w, b}{\text{max}}\frac{\underset{i=1, \dots, N}{\text{min}}v^{(i)} [w^T u^{(i)} + b]}{| w |}$$
具体来说,这将产生一个分类器,该分类器以较大的“间隙”将正和负训练样本分开。上述优化问题可以等效地写成
$$
\begin{array}{ll}
\underset{w,b,r}{\text{max}} & \frac{r}{| w |}\
\text{s.t.} & v^{(i)}[w^T u^{(i)} + b] \ge r, \quad i = 1, \dots, N
\end{array}
$$
出于许多原因,最重要的是为了易处理性,我们希望机器学习的公式化优化问题是凸的。然而,这两个公式都是非凸的,因为它们的目标函数是非凸的。幸运的是,观察到将w、b和r乘以一个比例因子不会改变上述问题的最优值,然后我们可以假设r = 1,并将其重新表述为
$$
\begin{array}{ll}
\underset{w,b}{\text{max}} & \frac{1}{| w |}\
\text{s.t.} & v^{(i)}[w^T u^{(i)} + b] \ge 1, \quad i = 1, \dots, N
\end{array}
$$
或等价地,
$$
\begin{array}{ll}
\underset{w, b}{\text{min}} & \frac{1}{2} | w |^2 \
\text{s.t.} & v^{(i)}[w^T u^{(i)} + b] \ge 1, \quad i = 1, \dots, N
\end{array}
$$
后者是一个凸优化问题。
现在我们应该提供一些关于为什么上述模型被称为支持向量机的解释。假设我们有大量的样本,也就是说,N很大。一旦我们通过识别最优$(w^ * , b ^ * )$来求解(1.4.5),我们将发现(1.4.5)的约束中只有少数在$(w^ * , b^ * )$处有效,即只有少数约束满足等式。相应的$u^(i)$被称为支持(支撑)向量。在几何学上,支持向量给出了所有训练样本到最优分离超平面($(w^ * )^T u + b^ * = 0$)的最短距离。如果我们沿着$w^{ * }/ \| w ^ * \|$的方向移动最优分离超平面,直到遇到一些训练样本,我们将找到第一组支持向量。类似地,沿着$- w^{ * }/ \| w ^ * \|$移动最优分离超平面,我们将获得另一组支持向量。这两组支持向量位于平行于最佳分离超平面的两个超平面上。它们定义了这两个不同类别的训练样本之间的差异,正好是(1.4.5)的目标值的两倍。
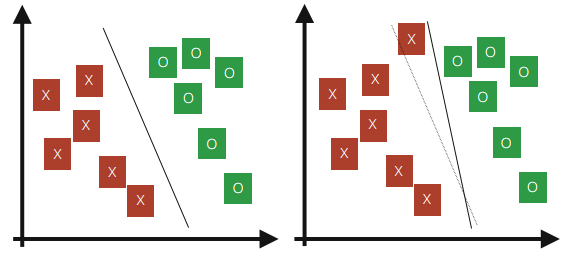
到目前为止,SVM的推导假设训练样本是线性可分的。然而,实际情况可能并非如此。此外,在某些情况下,我们并不清楚找到分离超平面是否正是我们想要的,因为这可能容易受到异常值的影响。为了看到这一点,图1.6a给出了一个最佳裕度分类器。然而,当在图1.6b中添加单个异常值时,最佳分离超平面戏剧性地摆动了,导致所得分类器的裕度小得多。
为了解决这些问题,对于一些$\lambda > 0$,我们将(1.4.5)重新表述为
$$
\begin{array}{ll}
\underset{w, b}{\text{min}} & \frac{1}{2} | w |^2 + \lambda \sum_{i = 1} ^N \xi_i \
\text{s.t.} & v^{(i)}[w^T u^{(i)} + b] \ge 1 - \xi_i, \quad i = 1, \dots, N \
& \xi_i \ge 0, \quad i = 1, \dots, N
\end{array} \tag {1.4.6}
$$
在上面的公式中,我们允许违反(1.4.5)中的约束,然后惩罚违反的总量。请注意,问题(1.4.6)可以等效地写成
$$\underset{w, b}{\text{min}} \quad \frac{1}{2} | w |^2 + \lambda \sum_{i = 1} ^N \text{max} { 0, 1 - v^{(i)}[w^T u^{(i)} + b]} \tag{1.4.7}$$
这些公式被称为软裕度支持向量机(soft-margin support vector machine)。
正则化、Lasso回归和岭回归
许多有监督机器学习模型,包括上面讨论的一些问题,都可以写成以下形式:
$$f^ * := \underset{x \in \Bbb{R}^n}{\text{min}}{ f(x) := \sum_{i=1}^N L(x^T u_i, v_i) + \lambda r(x) \tag{1.5.1} }$$
对于某些$\lambda \ge 0$,其中$L(\cdot, \cdot)$和$r(\cdot)$分别称为损失函数和正则化函数。
例如,在SVM中,我们有$x = (w, b), L(z, v) = \text{max}\{0, 1 -v z\}$和$r(x) = \| w \|^2$。在普通最小二乘回归中,我们有$x = 0, L(z, v) = (z - v)^2$,$r(\theta) = 0$。事实上,我们可以将许多不同类型的正则化添加到平方损失函数中,以避免过拟合,减少预测误差的方差,并处理相关的预测器。
两种最常用的惩罚模型是岭回归和Lasso回归。岭回归在(1.5.1)中,以$L(z, v) = (z - v)^2$,$r(x) = \| x \|_ 2 ^ 2$的形式给出,而Lasso回归以(1.5.1)表示,$L(z, v) = (z - v)^2$,$r(x) = \| x \|_ 1$。这里$\| x \|_ 2^2 = \sum_{i=1}^n x_i^2$,$\|x\|_ 1 = \sum_{i=1}^n |x_i|$。弹性网络结合了$l_1$和$l_2$罚函数,定义为
$$\lambda P_\alpha (\beta) = \lambda (\alpha |\beta|_ 1 + \frac{1}{2} (1 -\alpha) |\beta|_ 2 ^ 2)$$
当微调参数足够大时,Lasso回归导致稀疏解。随着微调参数$\lambda$的增加,所有系数都被设为零。由于将参数减少到零会将它们从模型中移除,因此Lasso是一个很好的选择工具。岭回归惩罚模型系数的$l_2$范数。它提供了更大的数值稳定性,并且比Lasso更容易、且更快计算。岭回归减少系数值的同时,惩罚增加,但不会将参数设为零。
变量选择在许多现代应用中非常重要,在这些应用中,$l_1$罚函数已被证明是成功的。因此,如果变量的数量很大,或者如果已知解是稀疏的,我们建议使用Lasso,它将选择足够高$\lambda$的少量变量,这对于模型的可解释性是至关重要的。$l_2$罚函数则没有这种效果:虽然缩小了系数,但没有将它们精确地设为零。
这两种罚函数在相关预测器的存在上也有所不同。$l_2$罚函数将相关列的系数相互缩小,而$l_1$罚函数倾向于只选择其中一个,并将其他系数设为零。使用弹性网络参数$\alpha$结合了这两种行为。弹性网既选择变量又保持分组效果(将相关列的系数收缩在一起)。此外,虽然可以进入Lasso模型的预测器的数量在$min(N, n)$达到饱和,其中N是观测值的数量,N是模型中变量的数量,但弹性网络没有这种限制,可以用更多的预测器来拟合模型。
总体风险最小化
让我们回到开始的例子。当朱莉检查她的决策过程时,她发现她的真正目标是设计决策函数来预测她对餐馆“竹园”的判断,而不仅仅是拟合历史数据。换句话说,她想要解决的问题并不是(1.1.1)中的问题。相反,她的问题可以更好地表述为
$$\underset{w, b}{\text{min}} \Bbb{E}_ {u, v} [h(u;w, b) - v]^2, \tag{1.6.1}$$
其中u和v是随机变量,表示朱迪和吉姆的评分,以及她自己对餐馆的判断。在此过程中,她含蓄地假设(1.1.1)的最优解将是(1.6.1)的一个很好的近似解。
事实上,朱莉的直觉可以得到更严格的证明。在随机优化中,(1.1.1)被称为(1.6.1)的样本平均近似(sample average approximation,SAA)问题。可以看出,随着N的增加,(1.1.1)的最优解将近似地解决问题(1.6.1)。值得注意的是,在机器学习中,问题(1.6.1)和(1.1.1)分别被称为总体和经验风险最小化(population and empirical risk minimization)。
还存在一些问题。首先,如果样本的维数和样本大小都很大,我们应该如何有效地解决问题(1.1.1)?第二,我们真的需要解决经验风险最小化问题吗?为什么我们不能设计一个算法来直接解决总体风险最小化问题?这些是我们以后主要讨论的问题。
神经网络
在过去的几年里,由于在语音识别、计算机视觉和文本处理方面取得了许多突破性的成果,深度学习在机器学习领域,尤其是在工业领域,已经产生了许多令人兴奋的东西。对于许多研究人员来说,深度学习是一组使用神经网络作为架构的算法的别称。尽管神经网络有着悠久的历史,但由于廉价的并行硬件(GPU、计算机集群)、大量的数据以及最近高效优化算法的发展,特别是那些为总体风险最小化而设计的算法,近年来它们变得更加成功。在这一节中,我们将从线性分类器的概念开始,逐步发展神经网络的概念。
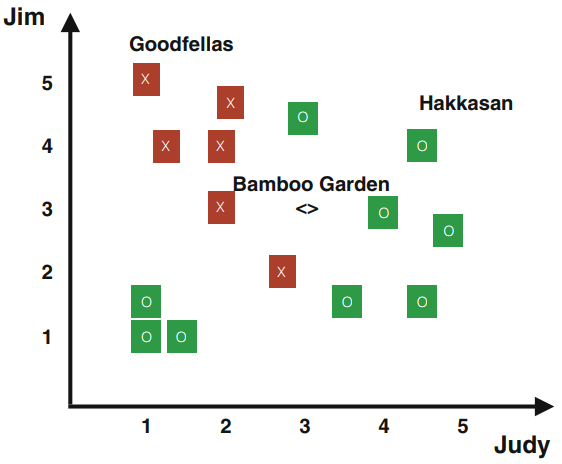
让我们继续讨论餐馆的例子。在前面的例子中,朱莉是幸运的,因为这些例子是线性可分的,这意味着她可以画一个线性决策函数来区分正负样本。她的朋友珍妮有不同的食物口味。如果绘制珍妮的数据,图表看起来将相当不同(见图1.7)。珍妮喜欢朱迪和吉姆认为很差的一些餐馆。问题是怎样才能为珍妮找出一个决策函数?通过查看数据,决策函数一定比我们之前看到的决策更复杂。解决复杂问题的启发式方法是把它分解成可解决的小问题。对于我们的特殊情况,我们知道如果把图左下角的“奇怪的”例子扔掉,那么问题就变得简单了。同样,如果我们把“奇怪”的例子放在右上角,问题也就简单了。我们使用我们假设的随机优化算法求解每种情况,决策函数如图1.8所示。
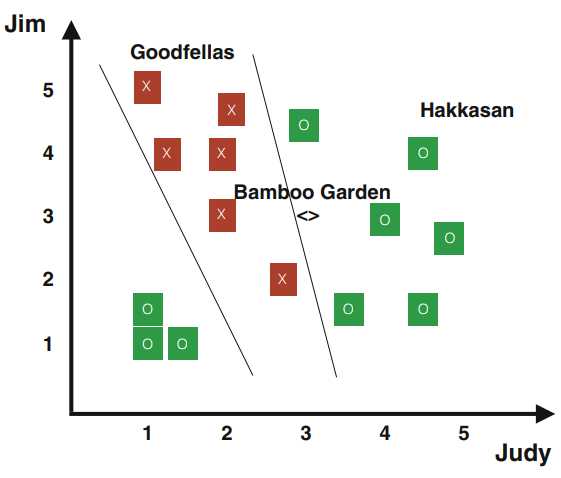
对于原始数据,是否有可能将这两个决策函数合并成一个最终决策函数?如上所述,我们假设两个决策函数是$h_1 (u) := g(w_1 u_1 + w_2 u_2 + b_1)$和$h_2 (u) := g(w_3 u_1 + w_4 u_2 + b_2)$,其中$g$表示(1.2.2)中定义的sigmoid函数。对于每个样本$u^{(i)}$,我们可以分别计算$h_1(u^{(i)})$和$h_2(u^{(i)})$。表1.3列出了与这些决策函数相关的数据。
| 餐馆 | 朱迪的评分 | 吉姆的评分 | 珍妮喜欢? |
|---|---|---|---|
| Goodfellas | $h_1(u^{(1)})$ | $h_2(u^{(1)})$ | 否 |
| Hakkasan | $h_1(u^{(2)})$ | $h_2(u^{(2)})$ | 是 |
| $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ |
| 竹园 | $h_1(u^{(n+1)})$ | $h_2(u^{(n+1)})$ | ? |
现在问题简化为找到一个新的参数集来加权这两个决策函数来近似$v$。让我们称这些参数为$\omega$,$c$,这样$h(u;w,b,\omega, c) := g(\omega_1 h_1(u) + \omega_2 h_2(u) + c)$可以近似标签$v$。这也可以表述为一个优化问题。总之,我们可以通过以下两个步骤找到珍妮的决策函数:
(a) 将数据分成两个集合。每个集合都可以通过线性决策简单地分类。然后使用前面的章节找到每个集合的决策函数;
(b) 使用新发现的决策函数,计算每个样本的决策值。然后将这些值作为另一个决策函数的输入。使用优化方法找到最终的决策函数。
图1.9提供了一种图形化的方式来可视化上述过程。
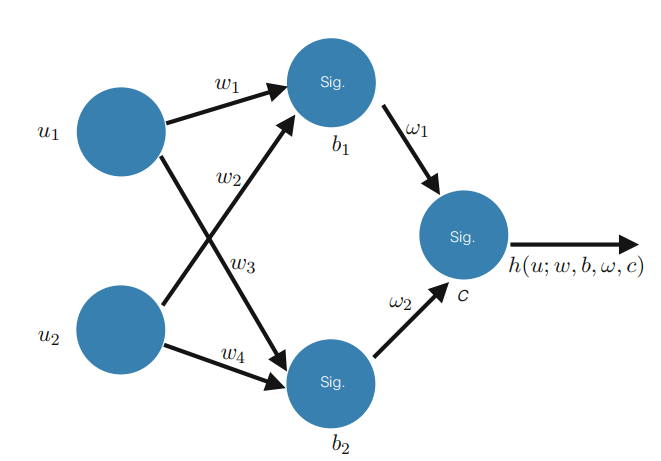
我们刚才讨论的是机器学习中一种特殊的结构,称为“神经网络”。这种神经网络有一个隐藏层,它有两个“神经元”。第一个神经元计算函数$h_1$的值,第二个神经元计算函数$h_2$的值。将实数值映射到0到1之间的有界值的sigmoid函数,也称为“非线性”或“激活函数”。由于我们使用的是sigmoid,激活函数也称为“sigmoid激活函数”。还有许多其他类型的激活函数。神经网络内部的参数,如$w$、$\omega$被称为“权重”,而$b$、$c$被称为“偏差”。如果我们有更复杂的函数要近似,我们可能需要更深的网络,也就是说,一个网络有更多的隐藏层,每个层有两个以上的神经元。
让我们回到为珍妮找到一个好的决策函数的问题上来。在上面的步骤中,当我们将数据集分成两组时,我们似乎有点作弊,因为我们查看了数据,并决定这两组应该以这种方式进行划分。有什么方法可以使这样的步骤自动化吗?事实证明,更自然的方法是在复杂的数据集中一次性找到参数$\omega$、$c$、$w$和$b$,而不是按顺序执行上述两个步骤。为了看得更清楚,让我们写下如何计算$h(u)$:
$$
\begin{aligned}
h(u) & = g(\omega_1 h_1(u; w_1, w_2, b_1) + \omega_2 h_2(u; w_3, w_4, b_2) + c) \
& = g(\omega_1 g(w_1 u_1 + w_2 u_2 + b_1) + ω_2 g(w_3 u_1 + w_4 u_2 + b_2) + c)
\end{aligned}
$$
我们将通过求解以下问题,同时找到参数$\omega_1$、$\omega_2$、$c$、$w_1$、$w_2$、$w_3$、$w_4$、$b_1$和$b_2$
$$\underset{\omega_1, \omega_2, c, w_1, w_2, w_3, w_4, b_1, b_2}{\text{min}} \Bbb{E}_ {u, v} [(h(u) - v)^2]$$
这个问题被证明是一个非凸随机优化问题。最大的问题仍然是:我们如何有效地解决这个问题,我们是否能为我们的解决过程提供任何保证?